
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика упругодеформируемых телСодержание книги
Поиск на нашем сайте
Все реальные тела деформируются. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. Различают два предельных случая деформации: упругие и пластические. Упругиминазываются деформации, исчезающие после прекращения действия приложенных сил.Пластическими деформациями называются такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия приложенных сил. Ограничимся изучением только упругих деформа- ций, считая тела идеально упругими. Такая идеализация возможна лишь для очень малых деформаций. Для них сущест- вует линейная зависимость между действующими силами и вызванными ими деформациями, подчиняющаяся закону Гука. Любая сложная деформация твердого тела может быть представлена как результат наложения более простых деформаций. Рассмотрим основные виды деформаций: одно- осное растяжение (сжатие) и сдвиг.
Одноосное растяжение и сжатие
Возьмём однородный стержень (рис.1.12) и приложим к его основаниям растягивающие (или сжимающие) усилия. Пусть lo - длина недеформированного стрежня, а S - его сечение. После приложения силы F его длина получает приращение Dl и делается равной l = l o + Dl. Отношение
называется относительным удлинением стержня. В случае растягивающих сил оно положительно, в случае сжимающих сил – отрицательно.
Рис.1.12 В любом поперечном сечении деформированного стержня возникнут нормальные упругие напряжения, численно равные упругой силе, приходящейся на единицу площади поперечного сечения тела, т.е.
Закон Гука для деформации растяжения (сжатия) имеет вид
Модуль Юнга зависит только от материала стержня и его физического состояния. При D l = l – l0 = l 0 и ε = 1 Е = σn . Поэтому, модуль Юнга равен тому нормальному напряжению, которое возникло бы в образце при увеличении его длины в 2 раза, если бы при такой деформации выполнялся закон Гука. Однако при таких больших деформациях закон Гука не выполняется и образец либо разрушается, либо нарушается пропорциональность между деформацией и силой. Под действием растягивающей или сжимающей силы изменяются не только продольные, но и поперечные размеры стержня. Характеристикой этого изменения является относи- тельное поперечное сжатие (растяжение)
где d - поперечный размер образца. При растяжении e < 0, при сжатии e >0. Отношение
называется коэффициентом Пуассон а. Для больших изотропных материалов он близок к 0,25. Модуль Юнга Е и коэффициент Пуассона m полностью характеризуют упругие свойства изотропного материала. Все прочие упругие постоянные могут быть выражены через Е и m. Деформированное тело обладает запасом потенциальной энергии. Эта энергия называется упругой. Она равна работе, затраченной на деформацию тела,
Объемная плотность упругой энергии W, т.е. энергия, приходящаяся на единицу объема растянутого (сжатого) стержня, равна
Сдвиг Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости, называемой плоскостью сдвига, смещаются параллельно друг другу (рис.1.13,а). Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД параллельная ВС, закреплена неподвижно (рис.1.13,б). При малом сдвиге:
где D х = СС’ - абсолютный сдвиг, а g - угол сдвига, называемый также относительным сдвигом. Закон Гука для деформации сдвигаимеет вид
где
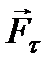
Модуль сдвига численно равен касательному напряже- нию, которое возникло бы в образце при относительном сдвиге, равном единице, если бы в этом случае выполнялся закон Гука. Между модулем сдвига, модулем Юнга и коэффициентом Пуассона существует cоотношение
Объемная плотность энергии упругой деформации при сдвиге, как и при растяжении, прямо пропорциональна квадрату напряжения и обратно пропорциональна модулю упругости:
Примеры решения задач на деформацию твердых тел Пример 1. Медная проволока длиной l = 80 см и сече- нием S = 8 мм2 закреплена одним концом в подвесном устрой- стве, а к её другому концу прикреплён груз массой m = 400 г. Вытянутую проволоку с грузом, отклонив до высоты подвеса, отпускают. Считая проволоку невесомой, определить её удлинение в нижней точке траектории движения груза. Модуль Юнга для меди Е = 118 ГПа. Решение Из закона Гука для продольного растяжения
где F – cила, растягивающая проволоку в нижней точке траектории груза. Она численно равна сумме силы тяжести и центростремительной силы, действующей на груз:
где υ – скорость груза. Согласно закону сохранения механической энергии,
Подставив найденное отсюда выражение для
Вычисляя, находим
Пример 2. Если на верхний конец вертикально располо- женной спиральной пружины положить груз, то пружина сожмётся на Δl =3мм. На сколько сожмёт пружину тот же груз, упавший на конец пружины с высоты h = 8 см? Решение В соответствии с законом сохранения механической энергии, полная энергия груза, падающего на пружину, равна энергии упругой деформации пружины при её сжатии. Полная энергия груза равна его потенциальной энергии U; при этом за нулевой уровень отсчёта потенциальной энергии примем положение сжатой пружины при падении груза (рис.1), тогда
где m – масса груза, g – ускорение свободного падения; k – жёсткость пружины. Если груз положить на пружину (рис.2), то в соответствии с законом Гука запишем:
В состоянии равновесия сила упругости равна силе тяже- сти груза
откуда
Подставляя полученное выражение для k в уравнение (1), получим:
Уравнение (3) можно преобразовать к виду
Тогда решение этого уравнения, удовлетворяющее физическому смыслу задачи (решением задачи будет являться лишь положительный корень), будет иметь вид:
Выполняя вычисления, получим
Пример 3. Из пружинного пистолета был произведён выстрел вертикально вверх. Определить высоту h, на которую поднимается пуля массой m = 20 г, если пружина жёсткостью k = 196 H/м была сжата перед выстрелом на x = 10 см. Массой пружины пренебречь. Решение Система пуля – Земля (вместе с пистолетом) является замкнутой системой, в которой действуют консервативные силы – силы упругости и силы тяготения. Поэтому для реше- ния задачи можно применить закон сохранения механической энергии. Согласно этому закону, полная механическая энергия E1 в начальном состоянии (перед выстрелом) равна полной энергии E2 в конечном состоянии (когда пуля поднялась на высоту h), т.е. E1 = E2, или T1+U1 = T2+U2, (1) где Т1 и Т2 – кинетическая энергия системы в начальном и конечном состояниях; U1 и U2 – потенциальные энергии в тех же состояниях. Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид U1 = U2. (2) Если потенциальную энергию в поле тяготения Земли на её поверхности принять равной нулю, то энергия системы в начальном состоянии равна потенциальной энергии сжатой пружины, т.е. Подставив приведённые выражения U1 и U2 в формулу (2), найдём
Произведя вычисления, получим h = 5 м.
1.8. Механика жидкостей и газов
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 676; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.46 (0.007 с.) |

 , (1.68)
, (1.68)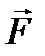
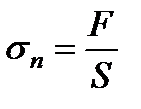 . (1.69)
. (1.69) , (1.70) где Е - модуль Юнга.
, (1.70) где Е - модуль Юнга. , (1.71)
, (1.71) , (1.72)
, (1.72)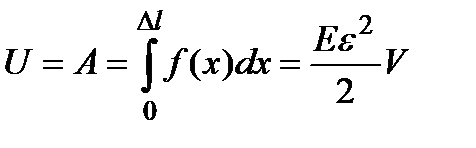 . (1.73)
. (1.73) . (1.74)
. (1.74)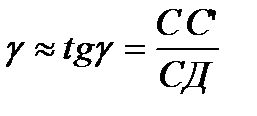 , (1.75)
, (1.75) , (1.76)
, (1.76) = F/S – скалывающее или тангенциальное напряжение, G - модуль сдвига.
= F/S – скалывающее или тангенциальное напряжение, G - модуль сдвига. . (1.77)
. (1.77)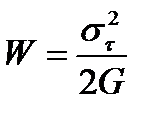 . (1.78)
. (1.78) , где
, где  - напряжение при упругой деформации, Е – модуль Юнга,
- напряжение при упругой деформации, Е – модуль Юнга, 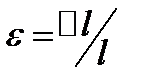 -относительное продольное растяжение, получим
-относительное продольное растяжение, получим , (1)
, (1) , (2)
, (2) .
. в формулу (2), получим
в формулу (2), получим 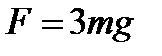 . Тогда из выражения (1) следу- ет, что искомое удлинение проволоки
. Тогда из выражения (1) следу- ет, что искомое удлинение проволоки .
.
 (1)
(1) . (2)
. (2) ,
,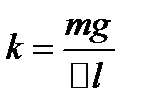 .
. Δl
Δl

 . (3)
. (3)


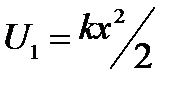 , а в конечном состоянии – потенци- альной энергии пули на высоте h, т.е.
, а в конечном состоянии – потенци- альной энергии пули на высоте h, т.е.  .
. или
или  .
.


