
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент силы. Основной закон динамики вращательного движения твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Момент силы характеризует ее вращательное действие. Различают момент силы относительно точки и относительно неподвижной оси. Моментом силы
Вектор Модуль момента силы равен M = F r sina = F l, (1.37) где a – угол между Моментом силы относительно неподвижной оси z называется скалярная величина Мz, равная проекции на эту ось вектора
Рис. 1.9 Рис. 1.10 Скорость изменения момента импульсачастицы со временем равна суммарному моменту сил, действующих на частицу:
Для твердого тела, вращающегося вокруг неподвижной оси Z, скорость изменения момента импульса тела Lz определяется действием результирующего момента всех внеш- них сил, относительно данной оси, т.е.
учитывая, что,
или
Уравнения (1.40) - (1.42) представляют собой уравнения динамики вращательного движения твердого тела относи- тельно неподвижной оси. Из последней формулы видно, что чем больше момент инерции тела, тем меньшее угловое ускорение оно приобретает под действием одного и того же момента внешних сил.
Первое уравнение описывает поступательное движение свободного тела со скоростью его центра масс. Второе уравнение описывает вращение твердого тела вокруг его центра масс.
Примеры решения задач по динамике поступательного и вращательного движения тел Пример 1. В системе, показанной на рисунке, массы тел равны
Решение Укажем все силы, действующие на грузы. Если считать нити, связывающие грузы, невесомыми и нерастяжимыми, а также пренебречь массой блоков, то силы натяжения нити с обеих сторон от каждого блока равны, в частности,
Выразим из уравнения (2) силу Т, получим
Приравняв правые части выражений (1) и (3), найдём
Откуда
Запишем уравнения движения грузов m1 и m2 в проекциях на ось oy:
Решая систему уравнений с учётом (4), получим
Пример 2. Моторная лодка массой m = 400 кг начинает двигаться по озеру. Сила тяги мотора F = 0,2 кН. Считая силу сопротивления пропорциональной скорости, определить скорость лодки через t = 20 с после начала её движения. Коэффициент сопротивления Решение На лодку в горизонтальном направлении действуют две силы: сила тяги мотора и сила сопротивления, величина которой пропорциональна скорости, т.е.
Для решения данного дифференциального уравнения разделим переменные
и выполним интегрирование:
Подставив пределы интегрирования, проведём преобразование
или
Окончательно получим
Произведя вычисления, найдем υ = 6.3 м /с. Пример 3. Через блок в виде диска массой m0 перекинута нить, к концам которой прикреплены грузы массами m1 и m2 (m2 > m1). Найти ускорение грузов. Трением пренебречь. Решение
На каждый из движущихся грузов действуют две силы: сила тяжести Уравнения движения этих тел в проекции на ось y имеют вид -m1a = m1g-T1, (1) m2a = m2g-T2. (2) Вращение блока вызывается действием сил натяжения нити, поскольку моменты сил тяжести блока и реакции оси равны нулю. Тогда основное уравнение динамики вращатель- ного движения для блока имеет вид
где R - радиус блока, Учтено также, что по третьему закону Ньютона силы натяжения нити с каждой из сторон блока одинаковы по модулю, т.е.
Если нить не проскальзывает относительно блока, то касательное ускорение его точек, соприкасающихся с нитью, равно ускорению нити в любой её точке, а следовательно а =εR. Решение системы полученных уравнений дает искомый результат
Пример 4. Однородный шар скатывается без скольже- ния с наклонной плоскости, образующей с горизонтом угол Решение На шар действует сила тяжести
 , (1) , (1)
где а – ускорение центра масс шара, Учитывая, что
Решая уравнения (1) и (3) совместно, получим
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.220 (0.007 с.) |

 относительно точкиО называется векторная величина
относительно точкиО называется векторная величина  равная векторному произведению радиус - вектора
равная векторному произведению радиус - вектора  , проведенного из точки О в точку прило- жения силы, на вектор силы:
, проведенного из точки О в точку прило- жения силы, на вектор силы: . (1.36)
. (1.36) перпендикулярен плоскости, в которой расположены векторы
перпендикулярен плоскости, в которой расположены векторы  , а его направление определяется также прави- лом правого винта (рис.1.9).
, а его направление определяется также прави- лом правого винта (рис.1.9). , определяемое длиной перпендикуляра, опущенного из точки О на линию действия силы.
, определяемое длиной перпендикуляра, опущенного из точки О на линию действия силы. момента силы
момента силы  – параллель- ную оси z,
– параллель- ную оси z,  – перпендикулярную оси z,
– перпендикулярную оси z,  – касательную к окружности радиуса R с центром на оси z. Вращательное действие оказывает только составляющая
– касательную к окружности радиуса R с центром на оси z. Вращательное действие оказывает только составляющая  = r Ft cos a = R Ft. (1.38)
= r Ft cos a = R Ft. (1.38)



 . (1.39)
. (1.39) , (1.40)
, (1.40)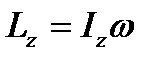 получим
получим , (1.41)
, (1.41) . (1.42)
. (1.42)
 Здесь m – масса тела, Ic – момент инерции тела относительно центра масс,
Здесь m – масса тела, Ic – момент инерции тела относительно центра масс,  , трения нет, массы блоков пренебрежимо малы. Найти ускорение тела массой
, трения нет, массы блоков пренебрежимо малы. Найти ускорение тела массой  относительно стола и ускорения грузов m1 и m2 относительно подвижного блока.
относительно стола и ускорения грузов m1 и m2 относительно подвижного блока.







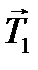







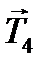

 ,
,  . Выберем положительные направления координатных осей х и y, запишем в скалярном виде уравнения движения груза
. Выберем положительные направления координатных осей х и y, запишем в скалярном виде уравнения движения груза  и системы грузов
и системы грузов  в соответствии со вторым законом Ньютона:
в соответствии со вторым законом Ньютона: ; (1)
; (1) . (2)
. (2)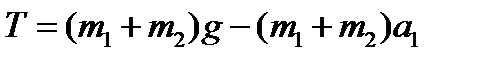 . (3)
. (3) .
. . (4)
. (4)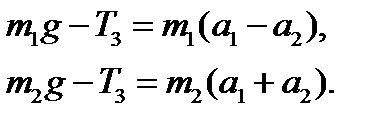
 .
. = 20 кг/с.
= 20 кг/с. . Уравнение движения лодки имеет вид:
. Уравнение движения лодки имеет вид: .
.
 .
.
 .
. .
.







 и сила натяжения нити
и сила натяжения нити  (см. рис.).
(см. рис.). , (3)
, (3)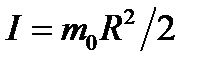 - его момент инерции, ε - угловое ускорение.
- его момент инерции, ε - угловое ускорение. .
.
 . Найдите ускорение центра инерции шара.
. Найдите ускорение центра инерции шара. , сила реакции
, сила реакции  и сила трения
и сила трения  . Последняя является силой трения покоя, которая и создает вращающий момент относительно мгновен- ной оси, проходящей через центр инерции. Под действием этих сил шар участвует в двух движениях (поступательном и вращательном), уравнения которых имеют следующий вид
. Последняя является силой трения покоя, которая и создает вращающий момент относительно мгновен- ной оси, проходящей через центр инерции. Под действием этих сил шар участвует в двух движениях (поступательном и вращательном), уравнения которых имеют следующий вид


 , (2)
, (2) - момент инерции шара относительно его центра масс,
- момент инерции шара относительно его центра масс, 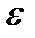 - угловое ускорение.
- угловое ускорение. ,
,  и
и  , преобразуем уравнение (2) к виду
, преобразуем уравнение (2) к виду . (3)
. (3) . (4)
. (4)


