
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электроемкость уединенного проводника.Содержание книги
Поиск на нашем сайте
Конденсаторы Проводник, удалённый от других тел, называется уединён- ным. При сообщении проводнику электрического заряда потенциал поля возрастает не только возле проводника, но и на его поверхности прямо пропорционально величине заряда. Коэффициент пропорциональности между q и φ называется электрической емкостью проводника
Электроемкость проводника численно равна величине заряда, который нужно сообщить данному проводнику для увеличения его потенциала на единицу. В СИ за единицу электроемкости принимают ёмкость 1 фарада – это емкость такого проводника, потенциал кото- рого изменяется на 1 В при сообщении ему заряда 1 Кл. Электроемкость уединенного проводника зависит от его формы и размеров, а также от диэлектрической проницаемости окружающей среды. Емкость не зависит ни от заряда провод- ника, ни от его потенциала, так как с увеличением q во столько же раз увеличивается j. Емкость проводника, имеющего форму шара радиуса R, погруженного в однородный диэлектрик с относительной диэлектрической проницаемостью e, равна
При сообщении проводнику А заряда q окружающие его проводники заряжаются через влияние, причем ближайшими к наводящему заряду q оказываются заряды противоположного знака (рис.4.14). Эти заряды ослабляют поле, созданное заря- дом q. Таким образом они понижают потенциал проводника А, а следовательно повышают его емкость. Идя по этому пути можно создавать приборы большой емкости, называемые конденсаторами. Конденсатор – система, состоящая из двух проводников (обкладок) c одинаковыми по модулю, но противоположными по знаку зарядами, форма и расположение которых таковы, что поле сосредоточено в узком зазоре между обкладками. Ёмкость конденсатора численно равна заряду, который нужно перенести с одного проводника на другой для измене- ния разности потенциалов между ними на единицу,
Она зависит от формы, размеров и взаимного располо- жения проводников, а также от диэлектрической проницае- мости среды. В зависимости от формы обкладок конденсаторы делятся на плоские, сферические, цилиндрические. Плоский конденсатор состоит из двух проводящих плоских пластин площадью S каждая, пространство между которыми заполнено диэлектриком с проницаемостью e. Если линейные размеры пластин велики по сравнению с расстоя- нием d между ними, то электростатическое поле между пластинами можно считать однородным. Емкость плоского конденсатора рассчитывается по формуле:
Емкость цилиндрического конденсатора
где l – длина обкладок конденсатора, Для получения нужной емкости конденсаторы соединяют параллельно или последовательно в батареи. При парал- лельном соединении (рис.4.15) U = const, а q =q1+q2+…+qn, поэтому
где При последовательном соединении (рис.4.16) q = const, U = U1+ U2 +……+Un, тогда
 . (4.46) . (4.46)
Рис. 4.14 Рис. 4.15 Рис. 4.16 Энергия электрического поля
Потенциальную энергию взаимодействия двух зарядов можно выразить через потенциалы полей этих зарядов
где j1 – потенциал, создаваемый вторым зарядом в точке расположения первого заряда; j2 – потенциал, создаваемый первым зарядом в точке расположения второго. Энергия взаимодействия точечных зарядов, в силу её аддитивности, равна сумме энергий каждой пары зарядов и определяется выражением
где jI - потенциал поля, создаваемого всеми зарядами, кроме qi , в точке нахождения заряда qi. Используя формулу (4.48), определим энергию заряжен- ного проводника и конденсатора. Так как проводник является эквипотенциальным, то
С учётом (4.40) можно получить и другие выражения для энергии заряженного проводника
Аналогичным образом, для энергии заряженного конденсатора в соответствии с (4.48) будем иметь
а, следовательно, и другие выражения
Электрическая энергия, определяемая формулой (4.51), может рассматриваться как энергия электростатического поля, существующего в конденсаторе. Поэтому есть смысл выразить эту энергию через напряжённость
получим
Поскольку поле плоского конденсатора однородно, то его объёмная плотность энергии определяется следующими выражениями
Зная плотность энергии поля в каждой точке, можно путём интегрирования найти энергию поля, заключённого в любом объёме V:
Примеры решения задач по электростатике Пример 1. Три одинаковых положительных заряда Решение Все три заряда, расположенные в вершинах треуголь- ника, находятся в одинаковых условиях, поэтому достаточно рассмотреть условие равновесия одного из трех зарядов, например В соответствии с принципом суперпозиции на заряд
где
Так как силы
Выразив F через
Применяя закон Кулона и имея в виду, что
откуда
Из геометрических построений в равностороннем треугольнике следует, что
С учетом этого формула (2) примет вид
После подстановки числовых значений получим
Пример 2. На тонком стержне длиной l =20 находится равномерно распределённый электрический заряд. На продолжении оси стержня на расстоянии a =10cм от ближай- шего конца находится точечный заряд Q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне. Решение Сила взаимодействия F заряженного стержня с точечным зарядом Q1 зависит от линейной плотности заряда τ на стержне. Зная эту зависимость, можно определить τ. При вычислении силы следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применять нельзя. В этом случае можно поступить следующим образом. Выделим на стержне малый участок dr с зарядом dQ = τdr (см рисунок).
Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,
Интегрируя это выражение в пределах от a до a+l, получаем
откуда
Произведём вычисления:
Пример 3. Два точечных электрических заряда Q1= 1 нКл и Q2 =-2 нКл находятся в воздухе на расстоянии d =10 см друг от друга. Определить напряжённость Е и потенциал φ поля, создаваемого этими зарядами в точке А, удалённой от заряда Q1 на расстоянии r1 = 9 см и от заряда Q2 на r2 = 7 см. Решение Согласно принципу суперпозиции электрических полей, каждый заряд создаёт поле независимо от присутствия в пространстве других зарядов. Напряжённость Напряжённости электростатического поля, создаваемого в воздухе (ε = 1) зарядами Q1 и Q2,
Вектор Модуль вектора
где α – угол между векторами
Подставляя выражение Е1 из (1) и Е2 из (2) в (3), получим
В соответствии с принципом суперпозиции электри- ческих полей потенциал φ результирующего поля, равен алгебраической сумме потенциалов
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
Согласно формулам (5) и (6) получим
или
Произведём вычисления: Е = 3,58 В/м, φ = - 157 В.
Пример 4. Электрическое поле создано двумя парал- лельными бесконечными заряженными плоскостями споверх- ностными плотностями заряда σ 1=0,4 мкКл/м2 и σ 2=0,1 мкКл/м2. Определить напряжённость электрического поля, созданного этими заряженными плоскостями. Решение
где, Плоскости делят всё прост- ранство на три области: I, II, III. Как видно из рисунка, в первой и третьей областях электрические силовые линии обоих полей направлены в одну сторону и следовательно, напряжённости суммарных полей Е(I) и Е(III) в первой и третьей областях равны между собой, противо- положно направлены и равны сумме напряжённостей полей, создаваемых первой и второй плоскостями:
Во второй области (между плоскостями) электрические силовые линии направлены в противоположные стороны и, следовательно, напряжённость поля Е(II) равна разности напряжённостей полей, создаваемых первой и второй плоскостями:
Подставив данные и произведя вычисления, получим
Пример 5. Две концентрические проводящие сферы радиусами R1 =6 см и R2 =10 см несут соответственно заряды Q1 = 1 нКл и Q2 = -0,5 нКл. Найти напряжённость Е поля в точках, отстоящих от центра сфер на расстояниях r1 =5 см, r2 =9 см, r3 = 15 см. Построить график Е(r).
Рис.1
Решение Точки в которых требуется найти напряжённости электрического поля, лежат в трёх областях (см. рис.1): область I (r1<R1), область II (R1< r2<R2), область III (r3>R2). 1. Для определения напряжённости Е1 в I области, проведём сферическую поверхность S1 радиусом r1 и восполь- зуемся теоремой Гаусса. Так как внутри области I зарядов нет, то получим
где En – нормальная составляющая напряжённости электри- ческого поля. Из соображения симметрии нормальная составляю- щая En должна быть равна самой напряжённости и постоянная для всех точек сферы, т.е. En =E1=const. Поэтому её можно вынести за знак интеграла:
Так как 2. В области II проведём сферическую поверхность радиусом r2. Так как внутри этой поверхности находится заряд Q1, то для неё, согласно теореме Гаусса, можно записать равенство
Так как En =E2=const, то из условий симметрии следует
откуда
Подставив сюда выражение для площади сферы, получим
3. В области III проведём сферическую поверхность радиусом r3. Эта поверхность охватывает суммарный заряд Q1+Q2. Cледовательно для неё теорема Гаусса имеет вид
Так как En =E3=const, то из условий симметрии следует
Выразив все величины в системе СИ и произведя вычисле- ния, получим
4. Построим график Е(r). В области I (r1<R1) напряжён- ность Е = 0. В области II (R 1< r1<R2) напряжённость Е2(r) изменяется по закону 1/ r2. В точке r = R1 напряжённость
В точке r = R2 (r стремится к R2 слева)
В области III (r>R2) Е3(r) изменяется по закону 1/ r2, причём в точке r=R2 (r стремится к R2 cправа)
Таким образом, функция Е(r) в точках r = R1 и r = R2 терпит разрыв. График зависимости Е(r) представлен на рис.2.
Пример 6. По тонкой нити, изогнутой по дуге окруж- ности, равномерно распределен заряд с линейной плотностью t =10 нКл/м. Определить напряженность Е и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина l нити составляет 1/3 длины окружности и равна 15 см. Решение
Определим напряжен- ность электрического поля в точке О. Для этого найдем сначала напряженность dE поля, создаваемого зарядом dQ:
Выразим вектор
где Напряженность Е найдем интегрированием. Интегриро- вание ведется вдоль дуги длиной l.
В силу симметрии где так как r=R = const,
(2)
Из этой формулы видно, что напряженность поля по направлению совпадает с осью Оу. Найдем потенциал электрического поля в точке О. Сначала найдем потенциал dj, поля создаваемого точечным зарядом dQ в точке О: dj =t dl /(4pe0 r).
Так как l = 2p R /3, то j =t /(6e0). (3) Произведя вычисления по формулам (2) и (3), получим
Пример 7. На тонком стержне длиной l равномерно распределен заряд с линейной плотностью t =10 нКл/м. Найти потенциал j, созданный распределенным зарядом в точке А, расположенной на оси стержня и удаленной от его ближай- шего конца на расстояние l. Решение
Потенциал dj, создаваемый этим точечным зарядом в точке А, можно определить по формуле
j = 62,4 В. Пример 8. Электрическое поле создаётся двумя зарядами Q1 = 4 мкКл и Q2 = -2 мкКл, находящиеся на расстоянии a =0,1 м друг от друга. Определить работу А12 сил поля по перемещению заряда Q = 50 нКл из точки 1 в точку 2 (см. рис.).
Решение

Для определения работы А12 сил поля воспользуемся соотно- шением
Применяя принцип супер- позиции электрических полей, определим потенциалы
Тогда
или
После подстановки численных значений, получим
Пример 9. С поверхностибесконечного равномерно заряженного (τ = 50 нКл/м) прямого цилиндра вылетает α – частица (υ0 = 0). Определить кинетическую энергию Т2 α - частицы в точке 2 на расстоянии 8 R от поверхности цилиндра.
Решение
Так как Е1= Т1+U1 и Е2= Т2+U2 (Т1 и Т2 – кинетические энергии α - частицы; а U1 и U2 – потенциальные), то, учитывая, что Т1 = 0 (υ1 =0), можно записать U1= Т2+U2, откуда: Т2= U1 - U2 = Q(φ1 - φ2), (1) где Q – заряд α - частицы, φ1 и φ2 – потенциалы точек 1 и 2. Для определения разности потенциалов воспользуемся соотношением между напряжённостью поля и изменением потенциала:
Интегрируя это выражение, найдём разность потенциалов двух точек, отстоящих на расстояниях r1 и r2 от оси цилиндра:
Так как цилиндр бесконечный, то для вычисления напряжённости поля можно воспользоваться формулой напряжённости поля, создаваемого бесконечно длинным цилиндром:
Подставив выражение для Е в уравнение (1), получим
или
Тогда, подставив выражение (3) в уравнение (1), получим
Проведём вычисления:
Пример 10. Электрон влетает в плоский горизонталь- ный конденсатор параллельно его пластинам со скоростью Решение Совместим начало координат с точкой, где находился электрон в момент его попадания в поле конденсатора. Движение электрона в конденсаторе можно представить как результат сложения двух прямолинейных движений: равно- мерного движения со скоростью Ускорение вдоль оси ОУ создает электростатическая сила (силой тяжести по сравнению с электростатической пренебрегаем)
Тогда уравнения, определяющие зависимость координат х и у и проекций скорости
В момент вылета из конденсатора
В момент вылета модуль скорости
Направление вектора определяется углом a, для которого, как видно из рисунка,
Подставляя числовые значения, получим
Пример 11. Конденсатор емкостью С1 =3 мкФ был заряжен до разности потенциалов U1 =40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью С2 =5 мкФ. Какая энергия W’ израсходуется на образование искры в момент присоединения второго конденсатора? Решение Энергия, израсходованная на образование искры, W’=W1-W2, (1) где W1 – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W2 – энергия, которую имеет батарея, составленная из двух конденсаторов. Энергия заряженного конденсатора определяется по формуле W= CU2/2, (2) где С – емкость конденсатора или батареи конденсаторов. Выразив в формуле (1) энергии W1 и W2 по формуле (2) и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим
где U2 – разность потенциалов на зажимах батареи конденса- торов.
(4)
или
Произведем вычисления:
Пример 12. Плоский воздушный конденсатор с площадью пластин S равной 500 см2, подключён к источнику тока, ЭДС которого равна ξ = 300 В. Определить работу А внешних сил по раздвижению пластин от расстояния d1 = 1 см до d2 =3 см в двух случаях: 1) пластины перед раздвижением отключались от источника тока; 2) пластины в процессе раздвижения остаются подключёнными к нему. Решение 1-й случай. Систему двух заряженных и отключённых от источника тока пластин можно рассматривать как изолиро- ванную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна изменению энергии системы:
где W1 – энергия поля конденсатора в начальном состоянии (пластины находились на расстоянии d1); W2 – энергия поля конденсатора в конечном состоянии (пластины находились на расстоянии d2). Энергию в данном случае удобно выразить через заряд Q на пластинах, так как заряд пластин, отключённых от источника при раздвижении не изменяется. Подставив в равенство (1) выражения
Выразив в этой формуле заряд через ЭДС источника тока и начальную электроёмкость С1
Подставляя в формулу (2) выражения электроёмкости (
Произведя вычисления по формуле (3), найдём
2-й случай. Пластины остаются подключёнными к источнику тока и система двух пластин уже не является изолированной. Воспользоваться законом сохранения энергии в этом случае нельзя. При раздвижении пластин конденсатора разность их потенциалов не изменяется (U=ξ), а ёмкость будет уменьшаться (
где Е1 – напряжённость поля, создаваемого зарядом одной пластины. Выразим напряжённость поля E1 и заряд Q через расстоя- ние x между пластинами:
Подставив эти выражения E1 и Q в равенство (4), получим
Проинтегрировав это равенство в пределах от d1 до d2, найдём выражение для искомой работы:
После упр
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.87 (0.011 с.) |

 . (4.40)
. (4.40) . (4.41)
. (4.41) . (4.42)
. (4.42) . (4.43)
. (4.43) , (4.44)
, (4.44) и
и 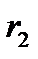 – радиусы коаксиальных цилиндров.
– радиусы коаксиальных цилиндров. , (4.45)
, (4.45) – емкость i – го конденсатора, n – число конденсаторов.
– емкость i – го конденсатора, n – число конденсаторов.
 , (4.47)
, (4.47) , (4.48)
, (4.48) . (4.49)
. (4.49) . (4.50)
. (4.50) ,
, . (4.51)
. (4.51) , характеризующую это поле. На основании соотношений
, характеризующую это поле. На основании соотношений и
и  ,
,
 . (4.52)
. (4.52) . (4.53)
. (4.53)
 нКл расположены в вершинах равносторон- него треугольника. Какой отрицательный заряд
нКл расположены в вершинах равносторон- него треугольника. Какой отрицательный заряд  нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах?
нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах? .
. , (1)
, (1) ,
,  ,
,  – силы, с которыми соответственно действуют на заряд
– силы, с которыми соответственно действуют на заряд  заряды
заряды  ,
,  и
и  ;
;  – равнодействующая сил
– равнодействующая сил 












 или
или  .
. и
и  и учитывая, что
и учитывая, что  .
. , найдем
, найдем ,
, . (2)
. (2) ,
,  .
. .
. нКл.
нКл. .
. ,
, .
. .
. электростати- ческого поля в искомой точке может быть найдена как геометрическая сумма напряжённостей
электростати- ческого поля в искомой точке может быть найдена как геометрическая сумма напряжённостей 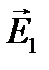 и
и  полей, создава- емых каждым зарядом в отдельности:
полей, создава- емых каждым зарядом в отдельности:  .
.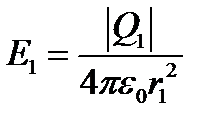 , (1)
, (1) . (2)
. (2) , (3)
, (3) .
.


 . (4)
. (4) . (5)
. (5) . (6)
. (6) ,
, .
.

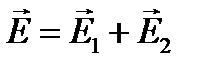 ,
, - напряженности электростатиче- ских полей, создаваемых первой и второй плоскостями соответст- венно.
- напряженности электростатиче- ских полей, создаваемых первой и второй плоскостями соответст- венно. или
или .
. , или
, или .
. ,
,  .
.



 (1)
(1) .
. , то Е1 =0, т.е. напряжённость электрического поля внутри первой сферы равна нулю.
, то Е1 =0, т.е. напряжённость электрического поля внутри первой сферы равна нулю. .
. , или
, или  ,
, .
.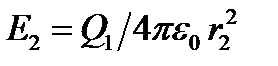 . (3)
. (3) .
. . (4)
. (4) ,
,  .
. .
. .
. .
. Выберем оси координат так, чтобы начало координат совпало с центром кривизны дуги, а ось Oy была бы симметрично расположена относительно концов дуги. На нити выделим элемент длины dl. Заряд dQ=t d l, находящийся на выделен- ном участке, можно считать точечным.
Выберем оси координат так, чтобы начало координат совпало с центром кривизны дуги, а ось Oy была бы симметрично расположена относительно концов дуги. На нити выделим элемент длины dl. Заряд dQ=t d l, находящийся на выделен- ном участке, можно считать точечным.
 – радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность.
– радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность. черезпроекции d E x и d E y на оси координат:
черезпроекции d E x и d E y на оси координат:
 ,
, и
и  – единичные векторы направлений (орты).
– единичные векторы направлений (орты).
 . Тогда
. Тогда  ,
,  (1)
(1) ,
, .
. Подставим
Подставим  в выражение (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:
в выражение (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до p/3, а результат удвоим: Выразив радиус R через длину l нити (3 l =2p R), получим
Выразив радиус R через длину l нити (3 l =2p R), получим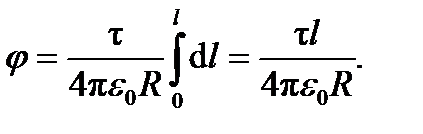

 В задаче рассматри- вается поле, создаваемое распределенным зарядом. В этом случае поступают следующим образом. На стержне выделяют малый участок длиной dx. Тогда на этом участке будет сосредоточен заряд dQ = t dx, который можно считать точечным.
В задаче рассматри- вается поле, создаваемое распределенным зарядом. В этом случае поступают следующим образом. На стержне выделяют малый участок длиной dx. Тогда на этом участке будет сосредоточен заряд dQ = t dx, который можно считать точечным.

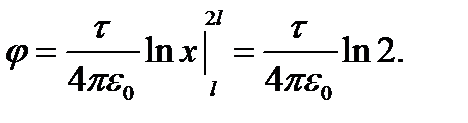

 точек 1 и 2 поля:
точек 1 и 2 поля: ;
; .
. ,
, .
. .
. . Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде
. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде , или
, или  .
. . (2)
. (2)
 ,
, . (3)
. (3)

 . Напряженность поля в конденсаторе
. Напряженность поля в конденсаторе  , длина конденсатора l=5см. Найти модуль и направление скорости электрона в момент вылета из конденсатора. На сколько отклонится электрон от первоначального направле-ния?
, длина конденсатора l=5см. Найти модуль и направление скорости электрона в момент вылета из конденсатора. На сколько отклонится электрон от первоначального направле-ния? в горизонтальном направлении и равноускоренного движения с некоторым ускорением
в горизонтальном направлении и равноускоренного движения с некоторым ускорением 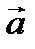 вдоль оси ОУ.
вдоль оси ОУ. ,
,


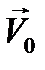


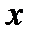

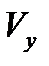


 и
и 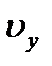 от времени, будут иметь вид:
от времени, будут иметь вид: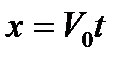 ,
,  , (1)
, (1) ,
,  . (2)
. (2) , y=h,
, y=h,  . Тогда получим
. Тогда получим ;
;  ;
;  . (3)
. (3) равен
равен . (4)
. (4) . (5)
. (5) м,
м,  ; tga=0,9; a»
; tga=0,9; a»  .
. (3)
(3) Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциа- лов U2 следующим образом:
Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциа- лов U2 следующим образом:

 .
. , (1)
, (1) и
и  , получим
, получим
 .
. , найдём
, найдём . (2)
. (2) и
и  ) плоского конденсатора, получим
) плоского конденсатора, получим . (3)
. (3) .
. ). Будут уменьшаться также заряд на пластинах конденсатора (Q=CU) и напряжённость электри- ческого поля (Е=U/d). Так как величины E и Q, необходи- мые для вычисления работы, изменяются, то работу следует вычислять путём интегрирования.
). Будут уменьшаться также заряд на пластинах конденсатора (Q=CU) и напряжённость электри- ческого поля (Е=U/d). Так как величины E и Q, необходи- мые для вычисления работы, изменяются, то работу следует вычислять путём интегрирования.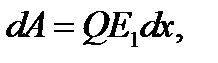 (4)
(4) и
и  , или
, или  .
. .
. .
.


