
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постулаты специальной теории относительностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для ответа на эти вопросы Майкельсоном был осуществ- лен его знаменитый опыт. В эксперименте Майкельсона использовалось движение Земли по ее орбите со скоростью 30км/с. Свет от источника S (рис.1.18) посылался в двух взаимно перпендикулярных направлениях, отражался от зеркал А и В, находящихся на одинаковом расстоянии от источника, и возвращался обратно. В этом опыте сравнивалось время прохождения светом обоих путей: SAS и SBS. Несмотря на то, что ожидаемая разность времен, определяемая в соответствии с законом сложения скоростей, была чрезвычайно мала, но прибор (интерферометр Майкель- сона) был достаточно чувствительным, чтобы эту разность надежно обнаружить. Тем не менее, результат опыта оказался отрицательным: разность времен не была обнаружена. Последующие, многочисленные опыты подтвердили первоначальный результат. Отрицательный результат опыта Майкельсона прежде всего показал, что скорость света не зависит от скорости источника. Если бы скорость света зависела от скорости источника, то разность времен была бы различима. Таким образом, было установлено, что скорость света в вакууме является величиной инвариантной, т.е. одинаковой во всех инерциальных системах отсчета. Глубокий анализ всего экспериментального и теорети- ческого материала, накопленного к тому времени, привел Эйнштейна к созданию специальной теории относительности, связавшей необычный характер распространения света с фундаментальными свойствами пространства и времени. В качестве исходных позиций специальной теории относитель- ности Эйнштейн принял два постулата, в пользу которых, прежде всего, свидетельствовал опыт Майкельсона. Эти постулаты носят название принципа относительности Эйнштейна и принципа постоянства скорости света. Первый постулат или принцип относительности Эйнштейна представляет собой обобщение принципа относи- тельности Галилея на любые физические процессы: все физические явления протекают одинаковым образом во всех инерциальных системах отсчета; все уравнения, выражаю- щие законы природы, инвариантны, т.е. не меняются, при переходе от одной инерциальной системы к другой. В соответствии с данным постулатом, все инерциальные системы отсчета эквивалентны по своим физическим свойствам. Никаким опытом нельзя в принципе выделить ни одну из них как предпочтительную, иначе говоря, абсолютной системы отсчета не существует. Второй постулат выражает принцип инвариантности скорости света: скорость света в вакууме не зависит от движения источника света и одинакова во всех направления, во всех инерциальных системах отсчета. Скорость света в вакууме является предельной, никакой сигнал, никакое воздействие одного тела на другое не могут распространяться со скоростью, превышающей скорость света в вакууме. Именно предельный характер этой скорости и объясняет одинаковость скорости света во всех системах отсчета. Постулаты специальной теории относительности противоречили классическим представлениям о свойствах пространства и времени, положенных в основу преобра- зований Галилея. В ньютоновской механике считалось само собой разумеющимся, что результаты измерений длины одного и того же стержня когда он покоится, и когда движется, относительно масштабной линейки совпадают. Эйнштейн же считал, что до опыта (a priori) по этому поводу ничего сказать нельзя. Эйнштейн также показал, что существование предель- ной скорости света приводит к тому, что понятие одновременности, считавшееся абсолютным, в действитель- ности является относительным. В разных системах отсчета время течет неодинаково. Кроме этого, Эйнштейн обратил внимание на то, что физической реальностью обладает не точка пространства и не момент времени, когда что-либо произошло, а только само событие. Для описания события в данной системе отсчета нужно указать место, в котором оно происходит, и момент времени, когда оно происходит.
1.9.3. Преобразования Лоренца. Следствия из преобразований Лоренца
Постулаты специальной теории относительности требовали новых правил перехода от одной инерциальной системы отсчета к другой. Такие правила, а именно, новые преобразования координат и времени были получены Лоренцем. Предположим, что происходит какое-то событие. В системе
Здесь с – скорость света, Из данных формул видно, что при При скоростях много меньших скорости света ( Наконец, при
Из преобразований Лоренца вытекает ряд необычных с точки зрения ньютоновской механики следствий. Сокращение длины. Рассмотрим стержень, расположен- ный вдоль оси  , ,
где
откуда получаем
Таким образом, длина стержня Замедление времени. Пусть в системе
отсюда получаем
В этой формуле Рассматривая прошедшее событие из системы
можно сказать, что движущиеся часы идут медленнее, чем покоящиеся Замедление времени является следствием постоянства скорости света во всех системах отсчета. Эффект замедления времени в настоящее время с высокой точностью подтверждается экспериментально. Относительность одновременности разнесенных в пространстве событий. Пусть в системе
Из полученных формул видно, что пространственно разобщенные Закон сложения скоростей. Ввиду того, что согласно преобразованиям Лоренца, изменяются не только координаты, но и время, меняется и закон сложения скоростей. Если в системе
В частности, положив в (1.98)
Этот результат не является удивительным, поскольку в основе преобразования Лоренца лежит инвариантность скорости света.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.011 с.) |

 оно характеризуется значением координат и времени (x,y,z,t). В системе
оно характеризуется значением координат и времени (x,y,z,t). В системе  (рис.1.17), движущейся относительно системы
(рис.1.17), движущейся относительно системы 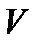 , направленной вдоль совпадающих осей
, направленной вдоль совпадающих осей  и
и  , - значениями координат и времени (
, - значениями координат и времени ( ). Формулы, связывающие штрихованные и нештрихованные значения координат и времени, имеют следующий вид
). Формулы, связывающие штрихованные и нештрихованные значения координат и времени, имеют следующий вид , (1.92)
, (1.92) . (1.93)
. (1.93) .
.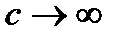 преобразова- ния Лоренца переходят в преобразования Галилея (1.88). Это означает, что различие в течение времени в разных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий.
преобразова- ния Лоренца переходят в преобразования Галилея (1.88). Это означает, что различие в течение времени в разных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий. ) преобразования Лоренца не отличаются от преобразований Галилея. Следовательно, преобразования Галилея не теряют своего значения, и могут быть использованы при малых по сравнению со скоростью света скоростях.
) преобразования Лоренца не отличаются от преобразований Галилея. Следовательно, преобразования Галилея не теряют своего значения, и могут быть использованы при малых по сравнению со скоростью света скоростях. выражения для координат и времени в формулах (1.92) и (1.93) становятся мнимыми, свидетель- ствуя о том, что движение со скоростями большими скорости света в вакууме невозможно. Невозможна и система отсчета, движущаяся со скоростью
выражения для координат и времени в формулах (1.92) и (1.93) становятся мнимыми, свидетель- ствуя о том, что движение со скоростями большими скорости света в вакууме невозможно. Невозможна и система отсчета, движущаяся со скоростью  , поскольку при
, поскольку при 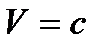 знаменатели формул (1.92) и (1.93) обращаются в нуль.
знаменатели формул (1.92) и (1.93) обращаются в нуль. и покоящийся относительно системы отсчета
и покоящийся относительно системы отсчета  (рис.1.19). Длина его в этой системе равна
(рис.1.19). Длина его в этой системе равна - не изменяющиеся со временем
- не изменяющиеся со временем  координаты концов стержня. Относительно системы
координаты концов стержня. Относительно системы  стержень движется вместе с системой
стержень движется вместе с системой  со скоростью
со скоростью  . Для определения его длины в этой системе нужно отметить координаты концов стержня в один и тот же момент времени
. Для определения его длины в этой системе нужно отметить координаты концов стержня в один и тот же момент времени  . Разность этих координат
. Разность этих координат 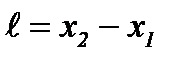 даст длину стержня, измеренную в системе
даст длину стержня, измеренную в системе  и
и  , воспользуемся преобразованиями Лоренца
, воспользуемся преобразованиями Лоренца ,
,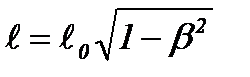 . (1.94)
. (1.94) , измеренная в системе, относительно которой он движется, оказывается меньше «собственной» длины
, измеренная в системе, относительно которой он движется, оказывается меньше «собственной» длины  , измеренной в системе, относи- тельно которой он покоится. Поперечные размеры стержня в обеих системах одинаковы. Итак, для неподвижного наблюдателя размеры движущихся тел в направлении их движения сокращаются, и тем больше, чем больше скорость движения.
, измеренной в системе, относи- тельно которой он покоится. Поперечные размеры стержня в обеих системах одинаковы. Итак, для неподвижного наблюдателя размеры движущихся тел в направлении их движения сокращаются, и тем больше, чем больше скорость движения. в одной и той же точке с координатой
в одной и той же точке с координатой  происходит какое-то событие, длящееся время
происходит какое-то событие, длящееся время  . Относительно системы
. Относительно системы  точка, в которой происходит это событие, перемещается. Согласно формулам (1.93), началу и концу события в системе
точка, в которой происходит это событие, перемещается. Согласно формулам (1.93), началу и концу события в системе 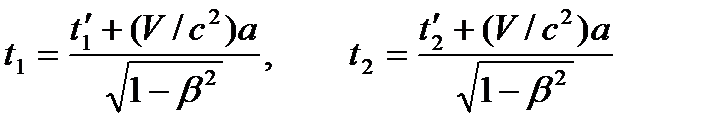 ,
, или
или  . (1.95)
. (1.95) - время, отсчитанной по часам, движущимся вместе с телом. Это время называется собственным временем и обычно обозначается буквой
- время, отсчитанной по часам, движущимся вместе с телом. Это время называется собственным временем и обычно обозначается буквой  . Время
. Время  измерено по часам системы, относительно которой тело движется со скоростью
измерено по часам системы, относительно которой тело движется со скоростью 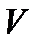 .
. - как длительность, измерен- ную по часам, движущимся вместе с телом. Представляя формулу (1.95) в виде
- как длительность, измерен- ную по часам, движущимся вместе с телом. Представляя формулу (1.95) в виде , (1.96)
, (1.96) . Эта зависимость особенно сильно проявляется при скоростях, сравнимых со скоростью света.
. Эта зависимость особенно сильно проявляется при скоростях, сравнимых со скоростью света. . В системе
. В системе  этим событиям будут соответствовать моменты времени
этим событиям будут соответствовать моменты времени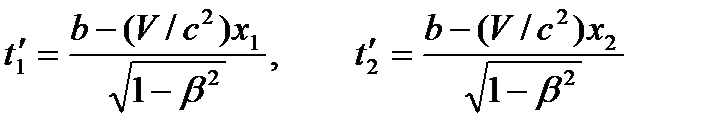 . (1.97)
. (1.97) и одновременные в системе
и одновременные в системе 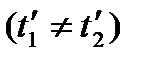 в системе
в системе  . При этом разность
. При этом разность  будет различна по величине и может отличаться по знаку в различных системах отсчета.
будет различна по величине и может отличаться по знаку в различных системах отсчета.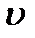 , имею- щей составляющие по осям координат
, имею- щей составляющие по осям координат  , то в системе
, то в системе  для составляющих скорости тела, получаем
для составляющих скорости тела, получаем . (1.98)
. (1.98) , получим
, получим . (1.99)
. (1.99)


