Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика поступательного и вращательного движения абсолютно твёрдого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При поступательном движении все точки абсолютно твердого тела за один и тот же промежуток времени соверша- ют одинаковые перемещения, скорости и ускорения всех точек тела одинаковы. Поэтому, чтобы описать поступательное движение абсолютно твердого тела, достаточно определить движение одной из его точек М, например, центра масс. При вращательном движении твердого тела все его точки движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения (рис.1.6). При этом радиус-векторы, проведенные из центров соответствующих окружностей к точкам тела за равные промежутки времени, поворачиваются на один и тот же угол. Угол поворота Dj любого из радиуc-векторов определяет угловой путь, пройден- ный телом за данный промежуток времени Dt. Очень малые углы поворота можно рассматривать как векторы Быстроту изменения углового перемещения с течением времени определяет угловая скорость
Угловая скорость является аксиальным вектором, кото- рый направлен вдоль оси вращения в соответствии с правилом правого винта. Быстроту изменения угловой скорости характеризует вектор углового ускорения
Направление вектора

Рис.1.6
Угловой путь, угловая скорость и угловое ускорение при равноускоренном вращении связаны между собой формулами, аналогичными формулам равноускоренного прямолинейного движения
где w0 – начальная угловая скорость. Кроме угловых характеристик, движение каждой точки вращающегося тела характеризуют линейные величины u, a, an, at (рис.1.7). Между угловыми и линейными характеристиками движения существуют следующие соотношения: u = w R, at = e R, an = w 2 R = Рис.1.7 Примеры решения задач по кинематике Пример 1. Движение частицы в плоскости ХУ описы- вается кинематическими уравнениями: Решение 1) Для нахождения уравнения траектории движения частицы необходимо исключить параметр
Полученное уравнение представляет собой уравнение параболы. 2) Вектор скорости частицы в момент времени
где Дифференцируя уравнения
и, следовательно, Модуль вектора скорости равен
Вектор ускорения представляет собой первую производ- ную от вектора скорости
где Следовательно, Знак «-» в полученном выражении свидетельствует о том, что ускорение направлено в сторону, противоположную оси У.
Модуль ускорения равен
3) Вектор средней скорости определяется выражением
где
Окончательно,
Пример 2. Камень брошен с вышки в горизонтальном направлении со скоростью υ = 30 м/c. Определить скорость, тангенциальное и нормальное ускорение камня в конце третьей секунды после начала движения. Решение Движение горизонтально брошенного тела под действием силы тяжести состоит из равномерного движения в горизон- тальном направлении со скоростью υx и свободного падения в вертикальном направлении со скоростью
Вектор полного ускорения тела
Как следует из рисунка, модуль нормального ускорения an тела равен: Тогда с учётом (1) получим
Модуль тангенциального ускорения
Выполняя вычисления, получим
Пример 3. Маховик, вращающийся с постоянной частотой Решение При равнозамедленном вращательном движении уравнения угловой скорости и углового пути имеют вид:
Решение этой системы уравнений дает соотношение, связывающее угловое ускорение с начальной
или Но так как
Подставив числовые значения в выражение (4), найдём
Угловое ускорение получилось отрицательным, так как маховик вращался замедленно. Продолжительность торможения определяем из уравнения (1):
С учетом (4) окончательно получим
Подставив числовые значения, найдем:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.33 (0.006 с.) |

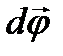 , совпадающие с осью, направление которых связано с направле- нием вращения тела правилом правого винта. Такие векторы называются аксиальными.
, совпадающие с осью, направление которых связано с направле- нием вращения тела правилом правого винта. Такие векторы называются аксиальными. =
=  . (1.16)
. (1.16)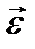 =
= 
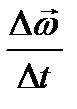 =
= 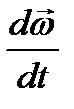 . (1.17)
. (1.17) >0) либо противоположно ему (при замедленном вращении
>0) либо противоположно ему (при замедленном вращении  , (1.18)
, (1.18)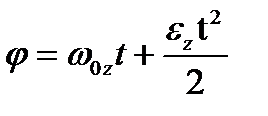 , (1.19)
, (1.19)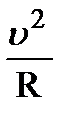 , (1.20)
, (1.20)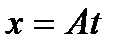 ;
; 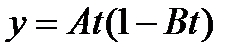 , где А и В – константы. Определить: 1) уравнение траектории
, где А и В – константы. Определить: 1) уравнение траектории 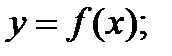 2) векторы скорости, ускорения и их численные значения; 3) вектор средней скорости за первые t секунд движения и его модуль.
2) векторы скорости, ускорения и их численные значения; 3) вектор средней скорости за первые t секунд движения и его модуль.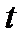 из кинематиче- ских уравнений:
из кинематиче- ских уравнений: .
. ,
,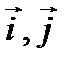 - единичные векторы вдоль осей Х и У, а
- единичные векторы вдоль осей Х и У, а 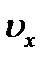 и
и 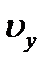 - проекции вектора скорости на соответствующие оси.
- проекции вектора скорости на соответствующие оси.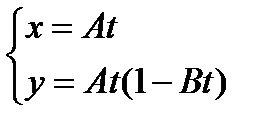 по времени, получим:
по времени, получим: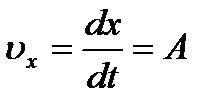 ;
; 
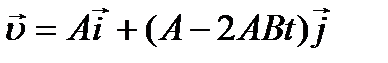 .
. .
.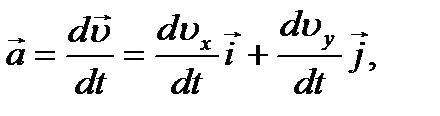
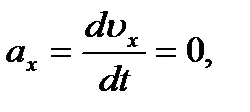
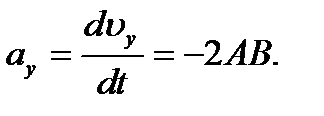
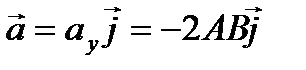 .
.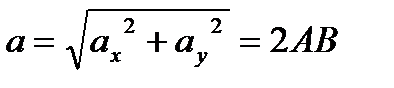 .
.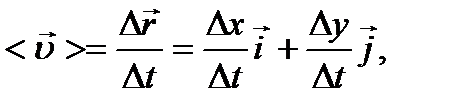
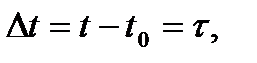 поскольку
поскольку 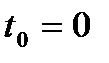 ,
, 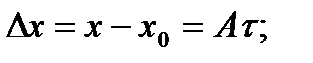
 .
.
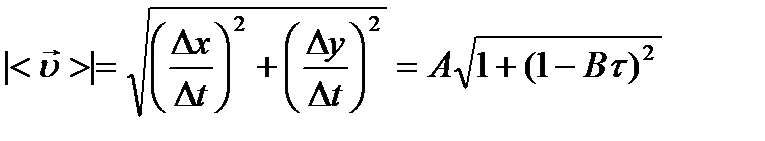 .
.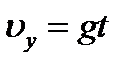 . Мгновенная скорость
. Мгновенная скорость 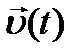 движения тела определяется сложением векторов
движения тела определяется сложением векторов 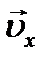 и
и 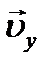 . Модуль скорости
. Модуль скорости 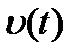 определим в соответ- ствии с теоремой Пифагора
определим в соответ- ствии с теоремой Пифагора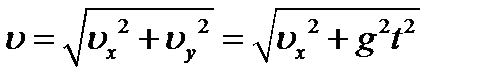 . (1)
. (1)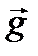 (ускорение свобод- ного падения) равен векторной сумме тангенциального
(ускорение свобод- ного падения) равен векторной сумме тангенциального 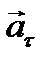 и нормального
и нормального  ускорений.
ускорений. .
.
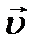
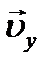
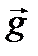
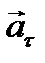
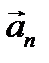
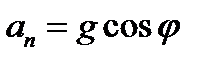 , где φ угол между векторами
, где φ угол между векторами  .
.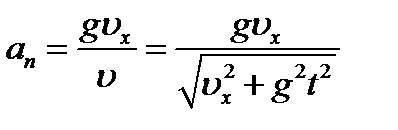 . (2)
. (2)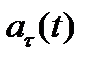 определим в соответствии с теоремой Пифагора:
определим в соответствии с теоремой Пифагора: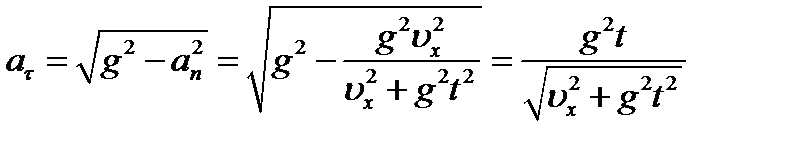 . (3)
. (3)

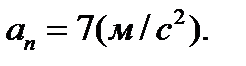
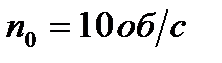 , при торможении начал вращаться равно- замедленно. Когда торможение прекратилось, частота враще- ния оказалась равной
, при торможении начал вращаться равно- замедленно. Когда торможение прекратилось, частота враще- ния оказалась равной  . Определить угловое ускоре- ние e маховика и продолжительность
. Определить угловое ускоре- ние e маховика и продолжительность  .
. , (1)
, (1)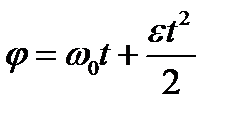 . (2)
. (2)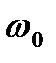 и конечной
и конечной 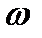 угловыми скоростями
угловыми скоростями ,
,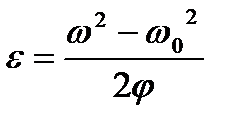 . (3)
. (3)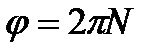 и
и 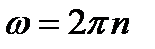 , то
, то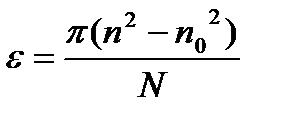 . (4)
. (4)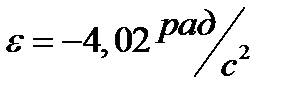 .
.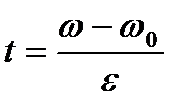 .
.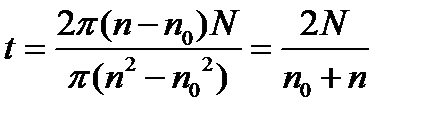 .
.