Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение молекул по скоростямСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В газе, находящемся в состоянии равновесия, устанав- ливается некоторое стационарное распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Пусть скорости dN молекул попадают в интервал от u до u+du. Относительное число молекул, скорости которых лежат в указанном интервале, отнесённое к ширине интервала du, называется функцией распределения молекул по скоростям
Функция распределения молекул газа по скоростям была получена Максвеллом и имеет следующий вид:
Здесь m0 - масса отдельной молекулы, k – постоянная Больцмана, T – температура. Тогда число молекул, скорости которых заключены в пределах от u до u+du, определяется выражением
где N – общее число молекул. График функции
Площадь заштрихованного участка
Выражение (2.12) представляет собой условие нормировки функции распределения молекул по скоростям. Конкретный вид функции зависит от рода газа и от температуры. С повышением температуры максимум функции смещается вправо (рис.2.2). Площадь же, ограниченная кривой, остается неизменной, поэтому с повышением темпера- туры кривая растягивается и понижается.
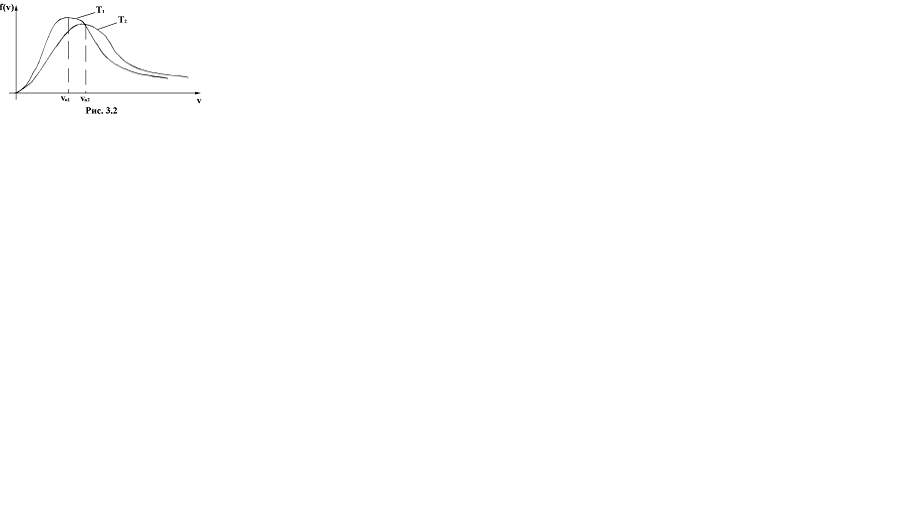
С ростом температуры увеличивается доля молекул, имеющих большую скорость. Скорость, при которой функция
где m0 - масса молекулы, М - молярная масса. Наряду с наиболее вероятной скоростью в молекуляр- но - кинетической теории пользуются понятием средней арифметической и средней квадратичной скорости:
Значение средней квадратичной скорости, рассчитан- ной по закону Максвелла, совпадает с ранее полученным выражением (2.8).
Барометрическая формула. Распределение Больцмана
Молекулы любого газа находятся в поле тяготения Земли. Если бы не было теплового движения молекул атмосферного воздуха, то все они упали бы на Землю. Если бы не было тяготения, то атмосферный воздух рассеялся бы во Вселенной. Тяготение и тепловое движение приводят газ в состояние, при котором его концентрация и давление убывают с высотой. Зависимость давления от высоты выражается формулой:
где p и p0 – давление газа на высотах h и h0 =0; M – молярная масса газа; R – универсальная газовая постоянная; T – температура. Используя (2.16) можно получить формулу для опреде- ления высоты по показаниям барометра
Эту формулу называют барометрической. Высоты обычно определяются относительно уровня моря, где давление считается нормальным. Уравнение (2.16) с учетом соотношения
Заменив
Из закона распределения Больцмана следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул. Закон Больцмана носит универсальный характер, он справедлив в любом внешнем потенциальном поле, а не только в поле сил тяжести.
Эффективный диаметр и средняя длина свободного Пробега молекул Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффектив- ным диаметром молекулы d (рис.2.3). В первом приближе- нии эффективный диаметр можно считать постоянным, хотя он и зависит от скорости сталкивающихся молекул, т.е. от температуры газа.
Расчет средней длины свободного пробега молекулы приводит к следующему соотношению
Здесь n – концентрация молекул, Таким образом, средняя длина свободного пробега молекул обратно пропорциональна их концентрации n, а при постоянной температуре, с учётом (2.19), обратно пропорцио- нальна давлению, т.е.
Зная среднюю длину свободного пробега молекулы можно определить и среднее число ее столкновений за одну секунду
Явления переноса Средняя длина свободного пробега l определяет такие свойства газов, как вязкость, теплопроводность и диффузия. Явление диффузии состоит в самопроизвольном проникновении и перемешивании молекул соприкасающихся газов, жидкостей и даже твёрдых тел. В химически однород- ном газе перенос массы вещества происходит при наличии градиента плотности и подчиняется закону Фика:
где M -масса вещества, диффундирующего за время t через площадку S, расположенную перпендикулярно градиенту плотности Явление теплопроводности состоит в переносе количе- ства теплоты в сторону убывания температуры. Этот процесс подчиняется закону Фурье:
где Q - количество теплоты, переносимое через площадку S за время t при градиенте температуры Коэффициент теплопроводностичисленно равен количе- ству теплоты, переносимой через единицу площади за единицу времени при температурном градиенте, равном единице. Вязкость (внутреннее трение) обусловлена возникнове- нием сил трения между слоями газа, перемещающимися парал- лельно друг другу с различными скоростями. Механизм возникновения внутреннего трения между слоями газа связан с обменом молекул между слоями, в результате которого происходит перенос импульса упорядоченного движения молекул из одного слоя в другой, что в свою очередь, приводит к торможению слоя, движущегося быстрее, и ускоре- нию слоя, движущегося медленнее. Внутреннее трение подчиняется закону Ньютона:
где h - коэффициент вязкости, Из формулы (2.24) следует, что коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади поверхности слоя при градиенте скорости равном единице. Выражения для коэффициентов диффузии, теплопровод- ности и внутреннего трения выводятся из молекулярно-кинетической теории.
где r -плотность газа, c v – удельная теплоёмкость газа при постоянном объёме,
Из формул (2.25) - (2.27) следуют простые зависимости между коэффициентами переноса:
Примеры решения задач по МКТ Пример 1. Определить молярную массу М смеси кислорода массой m = 25 г и азота массой m = 75 г. Решение Молярная масса смеси М есть отношение массы смеси m к количеству вещества смеси ν:
Масса смеси равна сумме масс компонентов смеси:
Количество вещества смеси равно сумме количеств вещества компонентов:
Подставляя в формулу (1) выражения m и ν, получим
Молярная масса кислорода М1 =32·10-3 кг/моль, азота М2 =28·10-3 кг/моль. Подставив значения величин в (2), получим М = 28,9·10-3 кг/моль. Пример 2. Определить число молекул N, содержащих- ся в объёме V =1 мм3 воды, и массу m 1 молекулы воды. Считать условно, что молекулы воды имеют форму шариков, соприка- сающихся друг с другом.
Решение Число N молекул, содержащихся в некоторой системе массой m, равно произведению постоянной Авогадро NA на количество вещества ν: N=νNA. Так как
Произведём вычисления, учитывая что М =18·10-3 кг/моль: N = 3,34·1019 молекул. Массу m1 можно найти по формуле m1 = M/NA. Подставив значения М и NA, найдём массу молекулы воды: m1 = 2,99·10-26 кг .
Пример 3. В баллоне объёмом 10 л находится гелий под давлением р1 =10 МПа и при температуре Т1 =300 К. После того как из баллона было взято m =10 г гелия, температура в баллоне понизилась до Т2 =290 К. Определить давление р2 гелия, оставшегося в баллоне. Решение Для решения задачи воспользуемся уравнением Менделе- ева – Клапейрона, применив его к конечному состоянию газа:
где m2 – масса гелия в баллоне в конечном состоянии; М – молярная масса газа; R – молярная газовая постоянная. Из уравнения (1) выразим искомое давление:
Массу m2 выразим через массу m1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона: m 2 = m1- m. (3) Массу m1 найдём из уравнения Менделеева – Клапейро- на, применив его к начальному состоянию газа:
Подставляя выражение массы m1 в (3), а затем выражение m2 в (2), найдём
или
Произведя вычисления, получим Р2 = 3,64·105 Па = 0, 364 МПа. Пример 4. В сосуде объёмом V =5 л находится азот массой m =1,4 г при температуре Т = 1800 К. Найти давление газа, имея в виду, что при этой температуре h = 30% молекул диссоциировано на атомы. Решение Так как часть молекул диссоциирована на атомы, то в сосуде находится смесь двух газов с молярными массами М 1=28·10-3 к г/моль и М 2 = М 1/2 =14·10-3 к г/моль. Уравнения состояния обоих газов имеют вид:
где P 1 и P 2 – парциальные давления молекулярного (N 2) и атомарного (N 1) азота. Давление смеси газов подчиняется закону Дальтона:
Сложим уравнения (1) и (2):
Так как m 1+ m 2= m (масса газа), то
Отсюда,
Пример 5. Какая часть молекул водорода, находящегося при температуре Т = 900 К, обладает скоростями, отличающи- мися от наиболее вероятной скорости не более, чем на 5 м/с? Решение Для решения задачи удобно воспользоваться распределе- нием молекул по относительным скоростям u:
где Наиболее вероятная скорость при Т = 900 К
Отсюда
Пример 6. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Считать температуру воздуха везде одинаковой и равной 10О С. Решение Зависимость давления от высоты имеет вид:
На уровне моря h0=0, поэтому Прологарифмируем обе части
Отсюда,
Пример 7. Найти среднюю продолжительность Решение Средняя продолжительность
Так как
Здесь n – концентрация молекул кислорода,
Из уравнения состояния идеального газа
тогда Эффективный диаметр молекул кислорода (величина справочная) d = 0,36 нм =
ТЕРМОДИНАМИКА
Термодинамика изучает общие свойства макроскопи- ческих систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |

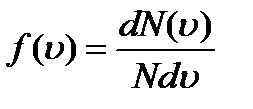 . (2.9)
. (2.9) . (2.10)
. (2.10)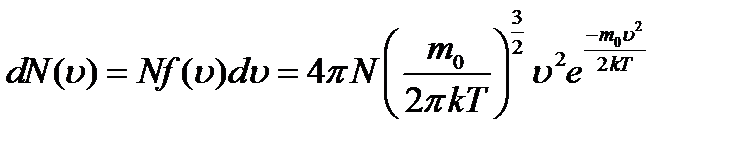 , (2.11)
, (2.11)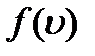 представлен на рис. 2.1.
представлен на рис. 2.1.
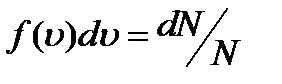 равна доле молекул, скорости которых лежат в интервале от u до u+du. Просуммировав доли молекул, во всем интервале скоростей, получим единицу. Это означает, что площадь, ограниченная функцией
равна доле молекул, скорости которых лежат в интервале от u до u+du. Просуммировав доли молекул, во всем интервале скоростей, получим единицу. Это означает, что площадь, ограниченная функцией 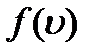 и осью абсцисс, равна единице
и осью абсцисс, равна единице . (2.12)
. (2.12)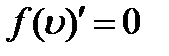 .
.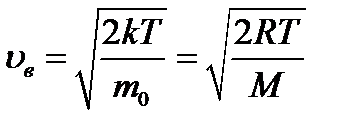 , (2.13)
, (2.13)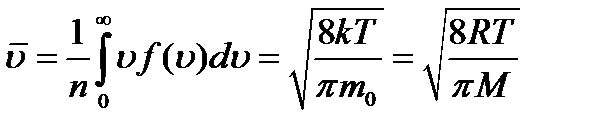 , (2.14)
, (2.14)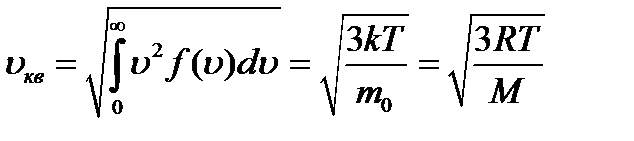 . (2.15)
. (2.15) , (2.16)
, (2.16) . (2.17)
. (2.17) можно записать в форме
можно записать в форме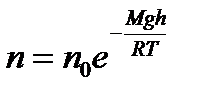 . (2.18)
. (2.18) и вводя потенциальную энергию молекулы в поле тяготения Земли
и вводя потенциальную энергию молекулы в поле тяготения Земли 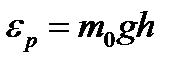 , получим закон распределе- ния Больцмана
, получим закон распределе- ния Больцмана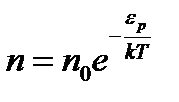 . (2.19)
. (2.19)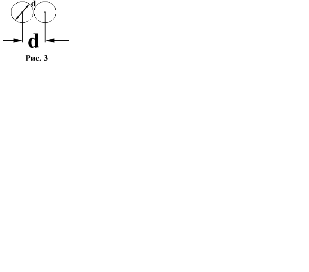
 . (2.20)
. (2.20)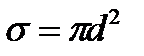 - эффективное сече- ние молекулы.
- эффективное сече- ние молекулы.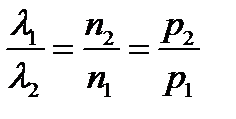 .
.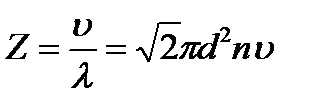 . (2.21)
. (2.21) (2.22)
(2.22) ; D - коэффициент диффузии. Знак «минус» показывает, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии численно равен массе молекул, переносимых через единичную площадку за единицу времени при градиенте плотности молекул равном единице.
; D - коэффициент диффузии. Знак «минус» показывает, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии численно равен массе молекул, переносимых через единичную площадку за единицу времени при градиенте плотности молекул равном единице.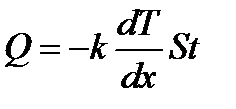 , (2.23)
, (2.23)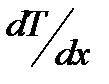 в направлении нормали к этой площади; k - коэффициент теплопроводности.
в направлении нормали к этой площади; k - коэффициент теплопроводности.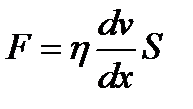 , (2.24)
, (2.24)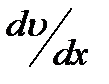 - градиент скорости в направлении перпендикулярном площадке S.
- градиент скорости в направлении перпендикулярном площадке S.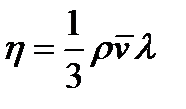 , (2.25)
, (2.25)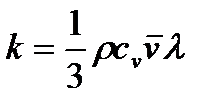 , (2.26)
, (2.26)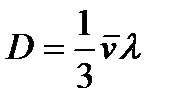 , (2.27)
, (2.27)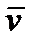 - средняя арифметическая скорость молекул, l -средняя длина свободного пробега.
- средняя арифметическая скорость молекул, l -средняя длина свободного пробега.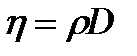 и
и 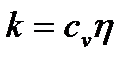 . (2.28)
. (2.28) . (1)
. (1)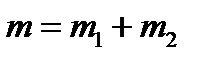 .
.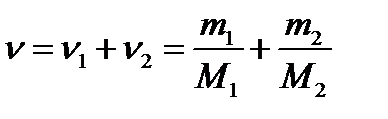 .
.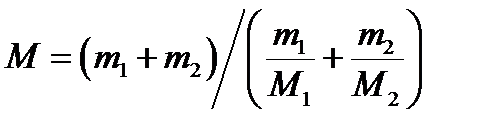 . (2)
. (2)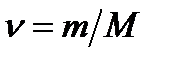 , где M – молярная масса, то
, где M – молярная масса, то 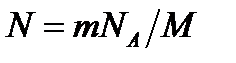 . Выразив в этой формуле массу как произведе- ние плотности на объём V, получим
. Выразив в этой формуле массу как произведе- ние плотности на объём V, получим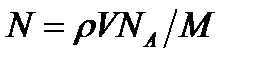 .
. , (1)
, (1)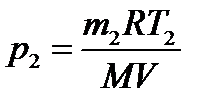 . (2)
. (2)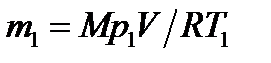 . (4)
. (4)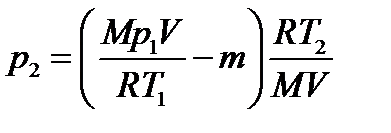 ,
,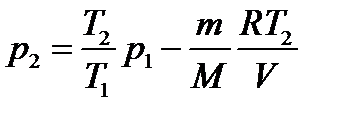 .
.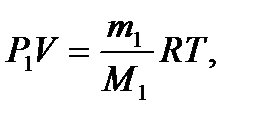 (1)
(1) (2)
(2)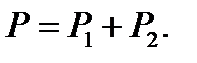
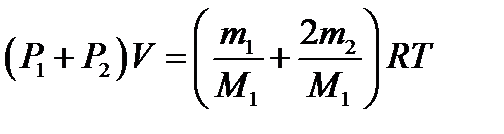 ,
,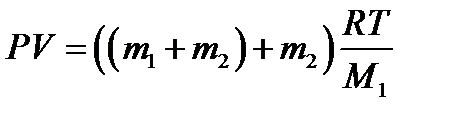 .
.
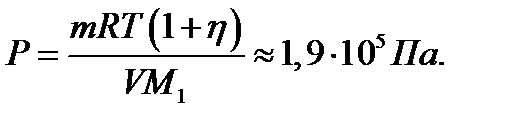
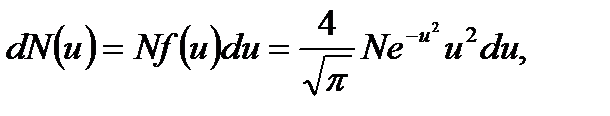
 Так как часть молекул обладает скоростями превышающими vв, а часть меньшими, чем νв, то
Так как часть молекул обладает скоростями превышающими vв, а часть меньшими, чем νв, то 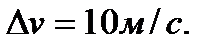
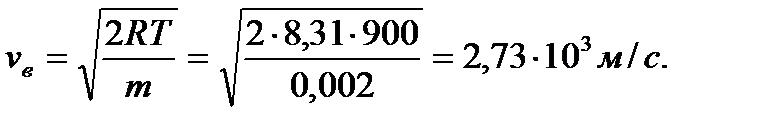
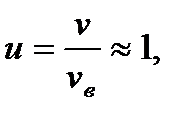


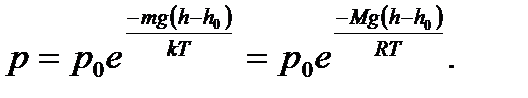

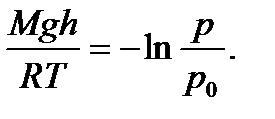
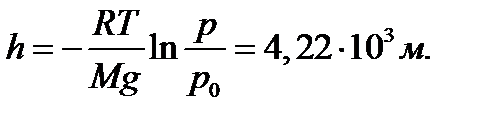
 свободного пробега молекул кислорода при температуре Т =250 К и давлении P =100 Па.
свободного пробега молекул кислорода при температуре Т =250 К и давлении P =100 Па.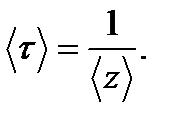
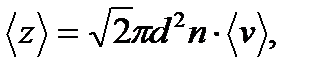 то
то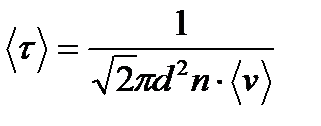 .
.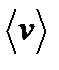 - средняя арифметическая скорость молекул кислорода.
- средняя арифметическая скорость молекул кислорода.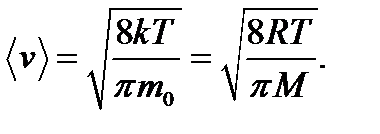
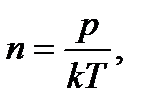
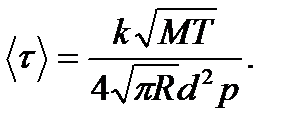
 . После подстановки числовых значений получим
. После подстановки числовых значений получим