Распределения Максвелла и Больцмана
Похожие статьи вашей тематики
№1  На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  - доля молекул, скорости которых заключены в интервале скоростей от v до - доля молекул, скорости которых заключены в интервале скоростей от v до  в расчете на единицу этого интервала. в расчете на единицу этого интервала.
Для этой функции неверными являются утверждения, что …
1.При понижении температуры величина максимума функции уменьшается
2.При понижении температуры площадь под кривой уменьшается
Решение: Полная вероятность равна:  то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости,  и которой функция и которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
 №2 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где №2 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до  в расчете на единицу этого интервала. в расчете на единицу этого интервала.
Для этой функции верными являются утверждения, что …
1.С увеличением температуры максимум кривой смещается вправо
2.При изменении температуры площадь под кривой не изменяется
№3
 Зависимости давления Зависимости давления  идеального газа во внешнем однородном поле силы тяжести от высоты идеального газа во внешнем однородном поле силы тяжести от высоты 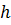 для двух разных температур представлены на рисунке. для двух разных температур представлены на рисунке.
Для графиков этих функций неверными являются утверждения, что …
1.Температура Т1 выше температуры Т2
2.Давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремиться к абсолютному нулю
Решение: Зависимость давления идеального газа от высоты  для некоторой температуры для некоторой температуры 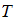 определяется барометрической формулой: определяется барометрической формулой:  , где , где  давление на высоте h=0, давление на высоте h=0,  масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура 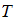 . Давление . Давление  определяется весом всего газа и не меняется при изменении температуры. определяется весом всего газа и не меняется при изменении температуры.
№4  На рисунке представлены графики зависимости концентрации молекул идеального газа На рисунке представлены графики зависимости концентрации молекул идеального газа  от высоты от высоты 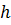 над уровнем моря для двух разных температур – над уровнем моря для двух разных температур –  (распределение Больцмана). (распределение Больцмана).
Для графиков этих функций верными являются утверждения, что …
1.Температура  выше температуры выше температуры 
2.Концентрация молекул газа на «нулевом уровне» (h=0) с повышением температуры уменьшается
Решение: Зависимость концентрации молекул идеального газа от высоты для некоторой температуры Т определяется распределением Больцмана:  где где  концентрация молекул на высоте h=0, концентрация молекул на высоте h=0,  масса молекулы, g - ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул масса молекулы, g - ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул  , и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: T2 >T1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» h=0 уменьшается, а на высоте h увеличивается. , и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: T2 >T1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» h=0 уменьшается, а на высоте h увеличивается.
 №5 На рисунке представлен график функции распределения молекул кислорода по скоростям(распределение Максвелла)для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь №5 На рисунке представлен график функции распределения молекул кислорода по скоростям(распределение Максвелла)для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь  плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей  в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что… в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что…
Решение:  Функция распределения Максвелла f( Функция распределения Максвелла f( имеет смысл плотности вероятности имеет смысл плотности вероятности  доля молекул, скорости которых заключены в интервале от доля молекул, скорости которых заключены в интервале от  до до  . В нашем случае d . В нашем случае d  вблизи вблизи  наиболее вероятной скорости молекул, близкой к которой движется большее число молекул dN-число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N-число молекул газа. Площадь заштрихованной полоски наиболее вероятной скорости молекул, близкой к которой движется большее число молекул dN-число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N-число молекул газа. Площадь заштрихованной полоски  определяет долю молекул,скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость определяет долю молекул,скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость  зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того,что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того,что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице  поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость  следовательно следовательно  . .
№6 Формула Больцмана  характеризует распределение частиц,находящихся в состоянии хаотического теплового движения,в потенциальном силовом поле,в частности распределение молекул по высоте в изотермической атмосфере.Соотнесите рисунки и соответствующие им утверждения… характеризует распределение частиц,находящихся в состоянии хаотического теплового движения,в потенциальном силовом поле,в частности распределение молекул по высоте в изотермической атмосфере.Соотнесите рисунки и соответствующие им утверждения…

Утверждения:
Распределение молекул по кинетическим энергиям Рис.1.
Распределение молекул воздуха в атмосфере Земли Рис.3.
Распределение молекул не является больцмановским и описывается функцией  Рис.2. Рис.2.
Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. Рис.1.
Распределение молекул в силовом поле при температуре T  . Рис.4. . Рис.4.
Решение:
Концентрация молекул в однородном поле силы тяжести убывает с высотой по закону  (распределение Больцмана на рис.3), где n-концентрация молекул на высоте (распределение Больцмана на рис.3), где n-концентрация молекул на высоте  , М-молярная масса, m- масса молекулы, g- ускорение свободного падения, R- универсальная газовая постоянная, k-постоянная Больцмана,T- температруа. В предельных случаях: если , М-молярная масса, m- масса молекулы, g- ускорение свободного падения, R- универсальная газовая постоянная, k-постоянная Больцмана,T- температруа. В предельных случаях: если  и молекулы равномерно распределяются по высоте (рис.1); если и молекулы равномерно распределяются по высоте (рис.1); если  и молекулы располагаются на нулевом уровне (рис.4). Если число молекул,имеющих большую потенциальную энергию,увеличивается по экспоненциальному закону и молекулы располагаются на нулевом уровне (рис.4). Если число молекул,имеющих большую потенциальную энергию,увеличивается по экспоненциальному закону  ,то такое распределение можно назвать «антибольцмановским», или инверсным. ,то такое распределение можно назвать «антибольцмановским», или инверсным.
 №7 На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где №7 На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от 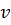 до до  в расчете на единицу этого интервала. Для этих функций верными являются утверждения, что … в расчете на единицу этого интервала. Для этих функций верными являются утверждения, что …
Решение: Функция Максвелла имеет вид  Полная вероятность равна: Полная вероятность равна:  , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости  , при которой функция , при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.
Ответ: распределение 1 соответствует газу, имеющему наибольшую массу молекул (при одинаковой температуре
Первое начало термодинамики
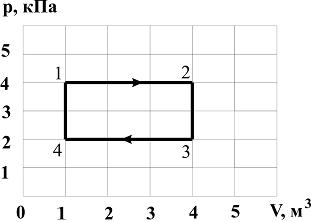 №1 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении по модулю равно … №1 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении по модулю равно …
Ответ 2
№2 При изотермическом расширении 0,5 моля газа при температуре 200 К объем увеличился в 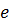 раз ( раз ( ). Работа газа (в Дж) равна … ). Работа газа (в Дж) равна …
Решение: При изотермическом расширении газа работа находится по формуле: 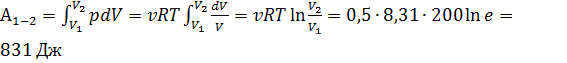
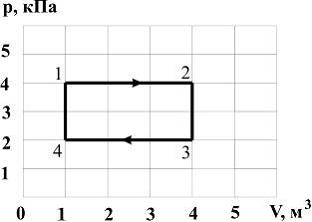 № 3 В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна № 3 В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна
Решение: Работа газа в координатных осях 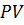 численно равна площади под графиком функции. Работа при нагревании совершается в процессе численно равна площади под графиком функции. Работа при нагревании совершается в процессе  . . 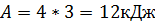 . .
 №4 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна … №4 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна …
Решение:
Работу газа в циклическом процессе можно найти, определив площадь, ограниченную кривой цикла в координатах p, V Цикл имеет форму трапеции. Тогда  . .
 №5 На (P,V)-диаграмме изображены 2 циклических процесса. №5 На (P,V)-диаграмме изображены 2 циклических процесса.
Отношение работ 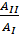 , совершенных в этих циклах, равно , совершенных в этих циклах, равно
Ответ 2.
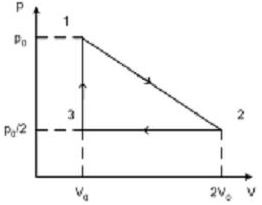 №6 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке … №6 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …
Решение.
Из графика видно, что газ получает теплоту в процессах 1-2 и 3-1. Переход 3-1 осуществляется при постоянном объеме, следовательно, работа газа 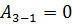 . Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к. . Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.  ; следовательно, ; следовательно,  и изменение внутренней энергии и изменение внутренней энергии  . По . По 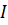 началу термодинамики для процесса 1-2 количество теплоты равно: началу термодинамики для процесса 1-2 количество теплоты равно:  , т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде. , т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.
№7 При увеличении давления в 3 раза и уменьшении объема в 2 раза внутренняя энергия идеального газа….
Решение. Внутренняя энергия идеального газа равна 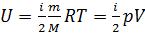 (учитываем, что (учитываем, что 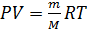 ), где ), где  давление, давление, 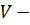 объем, объем, 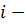 полное число степеней свободы, полное число степеней свободы,  универсальная газовая постоянная, универсальная газовая постоянная, 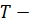 абсолютная температура, абсолютная температура, 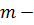 масса газа, масса газа, 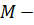 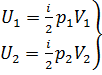 Учитывая, что Учитывая, что  , , 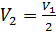 , получаем , получаем
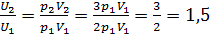 . Следовательно, . Следовательно, 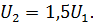
Ответ. Увеличится в 1,5 раза
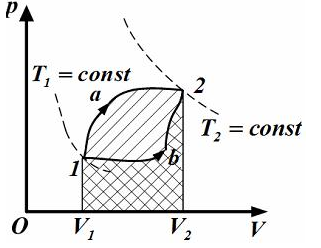  №8 Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2),как показано на рисунке.Теплота,полученная газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями… №8 Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2),как показано на рисунке.Теплота,полученная газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями…
Решение. При любом способе перехода идеального газа из первого состояния во второе,согласно первому началу термодинамики,теплота,сообщаемая газу,расходуется на изменение его внутренней энергии и на совершение им работы против внешних сил:  При этом изменение внутренней энергии,как однозначной функции термодинамического состояния системы, При этом изменение внутренней энергии,как однозначной функции термодинамического состояния системы, 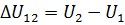 не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний: не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний: 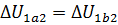 . Работа . Работа 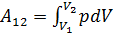 , совершаемая газом при изменение его объема от , совершаемая газом при изменение его объема от  , зависит от процесса перехода. Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p,V(см.рис.). , зависит от процесса перехода. Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p,V(см.рис.). 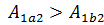 , так как площади заштрихованных фигур , так как площади заштрихованных фигур  . Следовательно по первому закону термодинамики: . Следовательно по первому закону термодинамики: 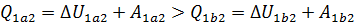 . Теплота,полученая газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями: . Теплота,полученая газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями:  . .
№9 Если при коэффициенте полезного действия тепловой машины 80 %, рабочее тело отдает холодильнику 200 Дж тепла, то получает от нагревателя ____ Дж тепла
Решение: Коэффициент полезного действия тепловой машины определяется по формуле 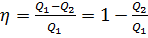 , где , где  – количество теплоты, полученное рабочим телом от нагревателя; – количество теплоты, полученное рабочим телом от нагревателя;  – количество теплоты, отданное рабочим телом холодильнику. – количество теплоты, отданное рабочим телом холодильнику. 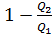 =0,8, =0,8,  , , 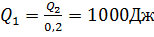 . .
№10 Идеальному газу сообщается одинаковое количество теплоты при изохорном (1), изобарном (2) и изотермическом (3) процессах. Для совершаемых газом работ справедливы соотношения …
Ответ 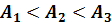 . .
№11 Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты 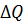 . На увеличение внутренней энергии газа расходуется часть теплоты . На увеличение внутренней энергии газа расходуется часть теплоты 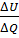 , равная … , равная …
Ответ 0,6
|



 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  - доля молекул, скорости которых заключены в интервале скоростей от v до
- доля молекул, скорости которых заключены в интервале скоростей от v до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала. то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости,
то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости,  и которой функция
и которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. №2 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
№2 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  до
до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала. Зависимости давления
Зависимости давления  идеального газа во внешнем однородном поле силы тяжести от высоты
идеального газа во внешнем однородном поле силы тяжести от высоты 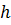 для двух разных температур представлены на рисунке.
для двух разных температур представлены на рисунке. для некоторой температуры
для некоторой температуры 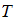 определяется барометрической формулой:
определяется барометрической формулой:  , где
, где  давление на высоте h=0,
давление на высоте h=0,  масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура
масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура  определяется весом всего газа и не меняется при изменении температуры.
определяется весом всего газа и не меняется при изменении температуры. На рисунке представлены графики зависимости концентрации молекул идеального газа
На рисунке представлены графики зависимости концентрации молекул идеального газа  от высоты
от высоты  (распределение Больцмана).
(распределение Больцмана). выше температуры
выше температуры 
 где
где  концентрация молекул на высоте h=0,
концентрация молекул на высоте h=0,  масса молекулы, g - ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул
масса молекулы, g - ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул  , и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: T2 >T1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» h=0 уменьшается, а на высоте h увеличивается.
, и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: T2 >T1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» h=0 уменьшается, а на высоте h увеличивается. №5 На рисунке представлен график функции распределения молекул кислорода по скоростям(распределение Максвелла)для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь
№5 На рисунке представлен график функции распределения молекул кислорода по скоростям(распределение Максвелла)для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь  плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей
плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей  в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что…
в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что… Функция распределения Максвелла f(
Функция распределения Максвелла f( имеет смысл плотности вероятности
имеет смысл плотности вероятности  доля молекул, скорости которых заключены в интервале от
доля молекул, скорости которых заключены в интервале от  до
до  . В нашем случае d
. В нашем случае d  вблизи
вблизи  наиболее вероятной скорости молекул, близкой к которой движется большее число молекул dN-число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N-число молекул газа. Площадь заштрихованной полоски
наиболее вероятной скорости молекул, близкой к которой движется большее число молекул dN-число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N-число молекул газа. Площадь заштрихованной полоски  определяет долю молекул,скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость
определяет долю молекул,скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость  зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того,что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице
зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того,что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице  поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость
поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость  следовательно
следовательно  .
. характеризует распределение частиц,находящихся в состоянии хаотического теплового движения,в потенциальном силовом поле,в частности распределение молекул по высоте в изотермической атмосфере.Соотнесите рисунки и соответствующие им утверждения…
характеризует распределение частиц,находящихся в состоянии хаотического теплового движения,в потенциальном силовом поле,в частности распределение молекул по высоте в изотермической атмосфере.Соотнесите рисунки и соответствующие им утверждения…
 Рис.2.
Рис.2. . Рис.4.
. Рис.4. (распределение Больцмана на рис.3), где n-концентрация молекул на высоте
(распределение Больцмана на рис.3), где n-концентрация молекул на высоте  , М-молярная масса, m- масса молекулы, g- ускорение свободного падения, R- универсальная газовая постоянная, k-постоянная Больцмана,T- температруа. В предельных случаях: если
, М-молярная масса, m- масса молекулы, g- ускорение свободного падения, R- универсальная газовая постоянная, k-постоянная Больцмана,T- температруа. В предельных случаях: если  и молекулы равномерно распределяются по высоте (рис.1); если
и молекулы равномерно распределяются по высоте (рис.1); если  и молекулы располагаются на нулевом уровне (рис.4). Если число молекул,имеющих большую потенциальную энергию,увеличивается по экспоненциальному закону
и молекулы располагаются на нулевом уровне (рис.4). Если число молекул,имеющих большую потенциальную энергию,увеличивается по экспоненциальному закону  №7 На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
№7 На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 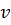 до
до  Полная вероятность равна:
Полная вероятность равна:  , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости  , при которой функция
, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. №1 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении по модулю равно …
№1 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении по модулю равно …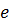 раз (
раз ( ). Работа газа (в Дж) равна …
). Работа газа (в Дж) равна …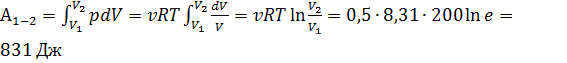
 № 3 В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна
№ 3 В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна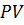 численно равна площади под графиком функции. Работа при нагревании совершается в процессе
численно равна площади под графиком функции. Работа при нагревании совершается в процессе  .
. 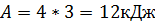 .
. №4 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна …
№4 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна … .
. №5 На (P,V)-диаграмме изображены 2 циклических процесса.
№5 На (P,V)-диаграмме изображены 2 циклических процесса.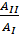 , совершенных в этих циклах, равно
, совершенных в этих циклах, равно №6 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …
№6 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …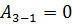 . Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.
. Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.  ; следовательно,
; следовательно,  и изменение внутренней энергии
и изменение внутренней энергии  . По
. По  началу термодинамики для процесса 1-2 количество теплоты равно:
началу термодинамики для процесса 1-2 количество теплоты равно:  , т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.
, т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.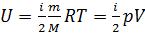 (учитываем, что
(учитываем, что 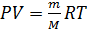 ), где
), где  давление,
давление, 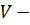 объем,
объем, 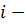 полное число степеней свободы,
полное число степеней свободы,  универсальная газовая постоянная,
универсальная газовая постоянная, 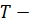 абсолютная температура,
абсолютная температура, 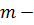 масса газа,
масса газа, 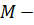
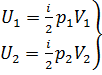 Учитывая, что
Учитывая, что  ,
, 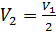 , получаем
, получаем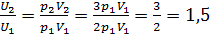 . Следовательно,
. Следовательно, 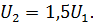

 №8 Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2),как показано на рисунке.Теплота,полученная газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями…
№8 Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2),как показано на рисунке.Теплота,полученная газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями… При этом изменение внутренней энергии,как однозначной функции термодинамического состояния системы,
При этом изменение внутренней энергии,как однозначной функции термодинамического состояния системы, 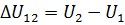 не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний:
не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний: 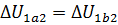 . Работа
. Работа 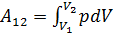 , совершаемая газом при изменение его объема от
, совершаемая газом при изменение его объема от  , зависит от процесса перехода. Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p,V(см.рис.).
, зависит от процесса перехода. Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p,V(см.рис.). 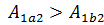 , так как площади заштрихованных фигур
, так как площади заштрихованных фигур  . Следовательно по первому закону термодинамики:
. Следовательно по первому закону термодинамики: 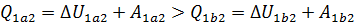 . Теплота,полученая газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями:
. Теплота,полученая газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями:  .
.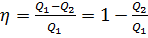 , где
, где  – количество теплоты, полученное рабочим телом от нагревателя;
– количество теплоты, полученное рабочим телом от нагревателя;  – количество теплоты, отданное рабочим телом холодильнику.
– количество теплоты, отданное рабочим телом холодильнику.  =0,8,
=0,8,  ,
, 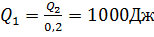 .
.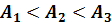 .
.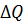 . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты 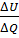 , равная …
, равная …


