
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика поступательного и вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (филиал) Федерального государственного бюджетного образовательного учреждения Высшего профессионального образования «Московский государственный университет дизайна и технологии» (НТИ (филиал) «МГУДТ»)
.
Методическое пособие для подготовки к интернет экзамену
НОВОСИБИРСК 2013
УДК 535 Б43 Авторы: Белоусова О.Е., Цыцилина О.
Методическое пособие создано по материалам интернет–тестирования в сфере образования на сайте http://www.i-exam.ru/index.html
Методическое пособие рассмотрено на заседании кафедры физики Протокол № _____ от _________ 2013 г.
Зав. кафедрой физики: О.Е. Белоусова
Рецензент: Краснолуцкий С.Л.
Содержание: 1. Кинематика поступательного и вращательного движения 2. Динамика поступательного и вращательного движения. 3. Работа. Энергия 4. Законы сохранения в механике 5. Элементы специальной теории относительности 6. Средняя энергия молекул 7. Распределения Максвелла и Больцмана 8. Первое начало термодинамики 9. Второе начало термодинамики. Энтропия. 10. Электростатическое поле в вакууме 11. Законы постоянного тока 12. Магнитостатика 13. Явление электромагнитной индукции 14. Электрические и магнитные свойства вещества 15. Свободные и вынужденные колебания 16. Сложение гармонических колебаний 17. Волны. Уравнение волны 18. Энергия волны. Перенос энергии волной 19. Уравнения Максвелла 20. Интерференция и дифракция света 21. Поляризация и дисперсия света 22. Тепловое излучение. Фотоэффект 23. Эффект Комптона. Световое давление 24. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга 25. Спектр атома водорода. Правило отбора 26. Уравнение Шредингера 27. Ядерные реакции. 28. Ядро. Элементарные частицы 29. Фундаментальные взаимодействия.
Ответ: 6
Ответ: 3 Ответ: 3
Ответ: 4 №7 Импульс материальной точки изменяется по закону Решение: Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе: №8 Импульс материальной точки изменяется по закону Решение: Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе: Ответ: 8
Ответ: 3
№10 Диск начинает вращаться вокруг неподвижной оси с постоянным угловым ускорением. Зависимость момента импульса диска от времени представлена на рисунке линией Ответ: B №11 Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Зависимость момента импульса диска от времени представлена на рисунке линией Ответ: Е №12 Тонкостенный цилиндр массы m и радиуса R вращается под действием постоянного момента сил вокруг оси, проходящей через центр масс цилиндра и перпендикулярной плоскости его основания. Если ось вращения перенести параллельно на край цилиндра, то (при неизменном моменте сил) его угловое ускорение Ответ: уменьшится в 2 раза …
Для моментов инерции рассматриваемых тел относительно указанных осей верным является соотношение Решение: Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси вычисляется по формуле
№14 Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил ( Решение: При вращении тела вокруг неподвижной оси момент относительно этой оси создает только одна составляющая действующей на него силы, а именно касательная к траектории точки ее приложения №15 При выстреле орудия снаряд вылетел из ствола с угловой скоростью Решение: Найдем угловые ускорения снаряда относительно продольной оси при выстреле №16 Шар, цилиндр (сплошной) и тонкостенный цилиндр с равными массами и радиусами раскрутили каждый вокруг своей оси до одной и той же угловой скорости и приложили одинаковый тормозящий момент. Раньше других тел остановится … Решение. При одинаковом моменте сил угловое ускорение обратно пропорционально моменту инерции тела. Момент инерции шара
№17 Тонкостенный цилиндр массы m и радиуса R вращается под действием постоянного момента сил вокруг оси, проходящей через центр масс цилиндра и перпендикулярной плоскости его основания. Если ось вращения перенести параллельно на край цилиндра, то (при неизменном моменте сил) его угловое ускорение Решение: Момент инерции при неизменных материале, форме и размерах тела зависит от расположения оси вращения. Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно его оси №18 Величина момента импульса тела относительно неподвижной оси изменяется по закону Решение:
№19 Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором Решение: По определению
№20 Частица совершила перемещение по некоторой траектории из точки M (1, 2) в точку N (2, –1). При этом на нее действовала сила Решение: По определению
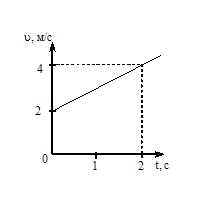
Ответ: №22 На рисунке приведен график зависимости скорости тела Ответ: 20 Работа. Энергия
Ответ: 250 №2 Тело массы m=100 г бросили с поверхности земли с начальной скоростью v0 = 10 м/с под углом α = 30° к горизонту. Если пренебречь сопротивлением воздуха, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна … Решение: Средняя мощность, развиваемая силой за некоторый промежуток времени, равна отношению работы, совершаемой силой за рассматриваемый промежуток времени, к длительности этого промежутка: Ответ: 0
№3 Потенциальная энергия частицы задается функцией (Функция Решение: Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид Ответ: 6 №4 Потенциальная энергия частицы задается функцией (Функция Ответ: -4 №5 Частица движется в двумерном поле, причем ее потенциальная энергия задается функцией Решение:
Решение:
№7 Тело массы Решение: Минимальная сила, которую надо приложить к телу, чтобы поднимать его по наклонной плоскости без ускорения, равна сумме составляющей силы тяжести, параллельной наклонной плоскости, и силы трения: минимальная работа 14 Дж.
Решение:
График зависимости имеет вид №9 Тело массой m =100 г бросили с поверхности земли вверх с начальной скоростью Решение: Работа силы сопротивления воздуха равна изменению полной энергии тела:
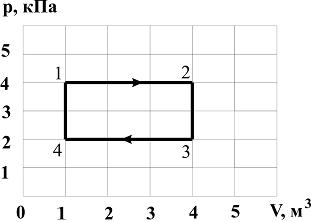
Средняя энергия молекул №1 Средняя кинетическая энергия молекул газа при температуре Решение: Д ля статической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная
№2 В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: №3 В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: Ответ: №4 Средняя кинетическая энергия молекулы идеального газа при температуре T равна Ответ:6 №5 Средняя кинетическая энергия молекул газа при температуре
№6 Если не учитывать колебательные движения в молекуле водяного пара, то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно … 1/2 №7 При комнатной температуре отношение Решение Из отношения №8 На каждую степень свободы движения молекулы проходится одинаковая энергия, равная Решение Средняя кинетическая энергия молекул равна Первое начало термодинамики
Ответ 2 №2 При изотермическом расширении 0,5 моля газа при температуре 200 К объем увеличился в Решение: При изотермическом расширении газа работа находится по формуле:
Решение: Работа газа в координатных осях
Решение: Работу газа в циклическом процессе можно найти, определив площадь, ограниченную кривой цикла в координатах p, V Цикл имеет форму трапеции. Тогда
Отношение работ
Ответ 2.
Решение. Из графика видно, что газ получает теплоту в процессах 1-2 и 3-1. Переход 3-1 осуществляется при постоянном объеме, следовательно, работа газа №7 При увеличении давления в 3 раза и уменьшении объема в 2 раза внутренняя энергия идеального газа…. Решение. Внутренняя энергия идеального газа равна
Ответ. Увеличится в 1,5 раза
Решение. При любом способе перехода идеального газа из первого состояния во второе,согласно первому началу термодинамики,теплота,сообщаемая газу,расходуется на изменение его внутренней энергии и на совершение им работы против внешних сил: №9 Если при коэффициенте полезного действия тепловой машины 80 %, рабочее тело отдает холодильнику 200 Дж тепла, то получает от нагревателя ____ Дж тепла Решение: Коэффициент полезного действия тепловой машины определяется по формуле
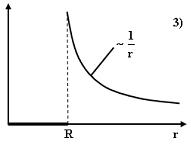
№10 Идеальному газу сообщается одинаковое количество теплоты при изохорном (1), изобарном (2) и изотермическом (3) процессах. Для совершаемых газом работ справедливы соотношения … Ответ №11 Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты Ответ 0,6 Ответ 7 №6 На рисунках представлены графики зависимости напряженности поля E(r) для различных распределений заряда:
График зависимости E(r) для заряженной металлической сферы радиуса R показан на рисунке Ответ. 2
Решение: Работа сил электростатического поля по перемещению заряда №8 Установите соответствие между источником электростатического поля и формулой,позволяющей вычислить напряденность поля в некоторой точке. 1.Точечный заряд 2.Равномерно заряженная длинная нить 3.Равномерно заряженная бесконечная плоскость Решение: Напряженность поля точечного заряда в некоторой точке обратно пропорциональна квадрату расстояния до зарядаю. Напряженность поля равномерно заряженной нити обратно пропорциональна расстоянию нити. Напряженность поля равномерно заряженной бесконечной плоскости не зависит от расстояния до плоскости. №9 Дана система точечных зарядов в вакууме и замкнутые поверхности Поток напряженности электростатического поля отличен от нуля сквозь… Решение: Согласно теореме Гасса,поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы их зарядов,охватываемых этой поверхностью,и электрической постоянной | ||
|
| Поделиться: |

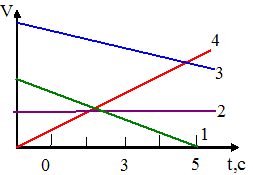 №16 На рисунке представлены графики зависимости скорости четырех тел, движущихся прямолинейно, от времени. Наибольшее перемещение за 5с совершено телом
№16 На рисунке представлены графики зависимости скорости четырех тел, движущихся прямолинейно, от времени. Наибольшее перемещение за 5с совершено телом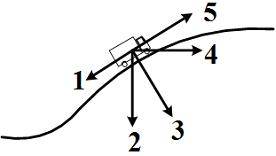 №6 Автомобиль поднимается в гору по участку дуги с увеличивающейся по величине скоростью. Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении
№6 Автомобиль поднимается в гору по участку дуги с увеличивающейся по величине скоростью. Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении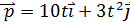 (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 4 c, равен
(кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 4 c, равен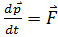 . Тогда зависимость силы от времени имеет вид
. Тогда зависимость силы от времени имеет вид 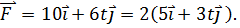 Модуль силы
Модуль силы  , и в момент времени t = 4 c
, и в момент времени t = 4 c 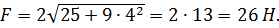
 (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 2 c, равен
(кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 2 c, равен .
. 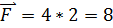
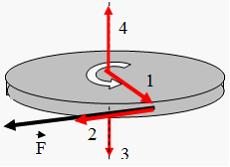 №9 Диск вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. К ободу диска приложена сила
№9 Диск вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. К ободу диска приложена сила 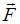 , направленная по касательной. Правильно изображает направление момента силы
, направленная по касательной. Правильно изображает направление момента силы 
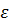 …
…
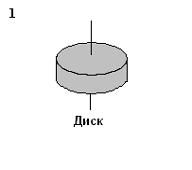
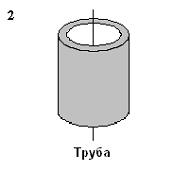 №13 Рассматриваются три тела: диск, тонкостенная труба и кольцо; причем массы m и радиусы R их оснований одинаковы.
№13 Рассматриваются три тела: диск, тонкостенная труба и кольцо; причем массы m и радиусы R их оснований одинаковы.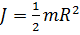 , тонкостенного кругового цилиндра массы m и радиуса R относительно его оси – по формуле
, тонкостенного кругового цилиндра массы m и радиуса R относительно его оси – по формуле 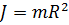 . Из последней формулы видно, что момент инерции тонкостенного цилиндра (трубы, кольца) не зависит от его высоты. Поэтому правильным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение
. Из последней формулы видно, что момент инерции тонкостенного цилиндра (трубы, кольца) не зависит от его высоты. Поэтому правильным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение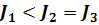
 или
или  ), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение
), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение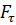 . Тогда момент силы относительно неподвижной оси равен:
. Тогда момент силы относительно неподвижной оси равен: 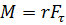 , где r – радиус-вектор точки приложения силы. В данном случае составляющая
, где r – радиус-вектор точки приложения силы. В данном случае составляющая 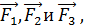 а для силы
а для силы  . Кроме того, все силы приложены в одной точке. Поэтому
. Кроме того, все силы приложены в одной точке. Поэтому 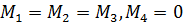 .
.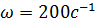 под углом
под углом 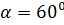 к горизонту. Момент инерции снаряда относительно его продольной оси
к горизонту. Момент инерции снаряда относительно его продольной оси 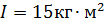 , расстояние между колесами орудия
, расстояние между колесами орудия  , время движения снаряда в стволе
, время движения снаряда в стволе 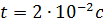 время выстрела, отличаются на …
время выстрела, отличаются на …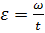 . Со стороны ствола орудия на снаряд действует момент сил
. Со стороны ствола орудия на снаряд действует момент сил  . По третьему закону Ньютона такой же по модулю, но противоположно направленный момент сил
. По третьему закону Ньютона такой же по модулю, но противоположно направленный момент сил 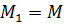 действует на ствол орудия. Его проекция на горизонтальную плоскость
действует на ствол орудия. Его проекция на горизонтальную плоскость 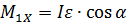 уравновешивается моментом, возникающим за счет различия сил реакций опоры (давление земли), действующих на колеса,
уравновешивается моментом, возникающим за счет различия сил реакций опоры (давление земли), действующих на колеса, 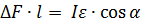 , где
, где 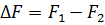 - разность сил реакций опор. Отсюда находим
- разность сил реакций опор. Отсюда находим 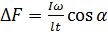 . Вычисляем
. Вычисляем 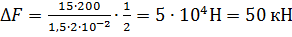 .
.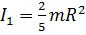 , момент инерции цилиндра
, момент инерции цилиндра 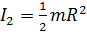 , момент инерции тонкостенного цилиндра
, момент инерции тонкостенного цилиндра 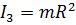 . Следовательно, ускорение торможения будет большим для шара и первым остановится шар.
. Следовательно, ускорение торможения будет большим для шара и первым остановится шар.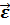 …
…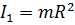 . При переносе оси момент инерции тела изменится. В соответствии с теоремой Штейнера
. При переносе оси момент инерции тела изменится. В соответствии с теоремой Штейнера  +
+  . Согласно основному уравнению динамики вращательного движения твердого тела относительно неподвижной оси, угловое ускорение равно:
. Согласно основному уравнению динамики вращательного движения твердого тела относительно неподвижной оси, угловое ускорение равно:  . Отсюда при неизменном моменте
. Отсюда при неизменном моменте  сил, действующих на тело, угловое ускорение
сил, действующих на тело, угловое ускорение 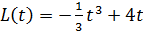 при этом зависимость величины момента сил, действующих на тело, описывается графиком…
при этом зависимость величины момента сил, действующих на тело, описывается графиком…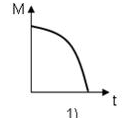 Скорость изменения момента импульса относительно какой-то неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, т.е.
Скорость изменения момента импульса относительно какой-то неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, т.е. 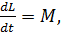 где L-величина момента импульса,M –величина момента сил. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента сил от времени
где L-величина момента импульса,M –величина момента сил. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента сил от времени 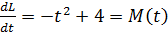 . Графиком этой функции является убывающая ветвь параболы.
. Графиком этой функции является убывающая ветвь параболы.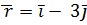 в точку 2 с радиус-вектором
в точку 2 с радиус-вектором 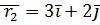 . При этом на нее действовала сила
. При этом на нее действовала сила  (радиус-векторы
(радиус-векторы 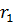 ,
, 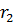 и сила
и сила  заданы в единицах СИ). Работа, совершенная силой
заданы в единицах СИ). Работа, совершенная силой  . С учетом того, что
. С учетом того, что 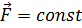 ,
,
 (координаты точек и сила
(координаты точек и сила 
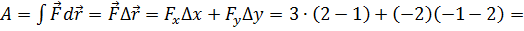
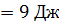
 № 21 Мальчик тянет санки массой m по горизонтальной поверхности с ускорением
№ 21 Мальчик тянет санки массой m по горизонтальной поверхности с ускорением 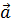 , при этом веревка натягивается силой
, при этом веревка натягивается силой 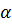 к горизонту. Если коэффициент трения полозьев о поверхность равен
к горизонту. Если коэффициент трения полозьев о поверхность равен  , то уравнение движения санок в проекции на направление движения санок имеет вид …
, то уравнение движения санок в проекции на направление движения санок имеет вид …
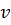 от времени t. Масса тела 20 кг. Сила (в H), действующая на тело, равна
от времени t. Масса тела 20 кг. Сила (в H), действующая на тело, равна №1 На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Момент импульса первого тела L1 = 0,1 Дж·с. Если m = 1 кг, R = 10 см, то кинетическая энергия второго тела (в мДж) равна
№1 На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Момент импульса первого тела L1 = 0,1 Дж·с. Если m = 1 кг, R = 10 см, то кинетическая энергия второго тела (в мДж) равна Работа силы тяжести
Работа силы тяжести  и
и 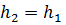 по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю.
по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю. .
.  - компонента (в Н) вектора силы, действующей на частицу в точке А(1, 2, 3), равна
- компонента (в Н) вектора силы, действующей на частицу в точке А(1, 2, 3), равна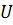 и координаты точки А заданы в единицах СИ.)
и координаты точки А заданы в единицах СИ.)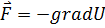 , или
, или 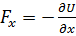 ,
, 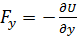 ,
, 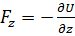 . Таким образом,
. Таким образом, 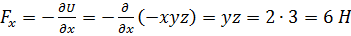 .
.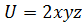 .
. 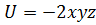 . Работа сил поля (в Дж) по перемещению частицы из точки С (1, 1, 1) в точку В (2, 2, 2) равна …
. Работа сил поля (в Дж) по перемещению частицы из точки С (1, 1, 1) в точку В (2, 2, 2) равна … Дж
Дж №6 Тело движется вдоль оси
№6 Тело движется вдоль оси 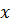 под действием силы, зависимость которой от координаты
под действием силы, зависимость которой от координаты 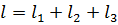 определяется выражением …
определяется выражением … Работа переменной силы в случае одномерного движения на участке
Работа переменной силы в случае одномерного движения на участке 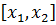 определяется как интеграл:
определяется как интеграл: 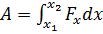 . На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:
. На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту: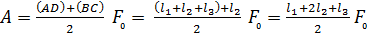 .
.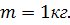 поднимают по наклонной плоскости. Высота наклонной плоскости
поднимают по наклонной плоскости. Высота наклонной плоскости 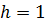 м, длина ее основания
м, длина ее основания 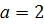 м, коэффициент трения
м, коэффициент трения  . Минимальная работа, которую надо совершить, в джоулях равна …
. Минимальная работа, которую надо совершить, в джоулях равна …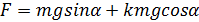 . Работа равна
. Работа равна  , где
, где  – длина наклонной плоскости. Учитывая, что
– длина наклонной плоскости. Учитывая, что 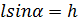 и
и  , получим
, получим 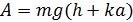 . Следовательно,
. Следовательно,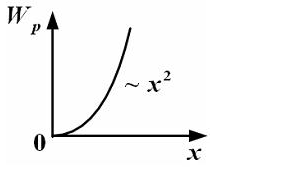 №8 На рисунке показан график зависимости потенциальной энергии
№8 На рисунке показан график зависимости потенциальной энергии  от координаты х. График зависимости проекции силы F(x)от координаты х имеет вид…
от координаты х. График зависимости проекции силы F(x)от координаты х имеет вид…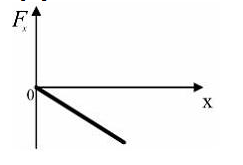 Потенциальная энергия,как видно из графика, пропорциональна квадрату координаты
Потенциальная энергия,как видно из графика, пропорциональна квадрату координаты 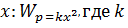 - коэфициент пропорциональности. Проекция силы F(x)на ось Х связана с потенциальной энергией соотношением
- коэфициент пропорциональности. Проекция силы F(x)на ось Х связана с потенциальной энергией соотношением  и равна
и равна 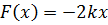
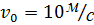 . Высота подъема тела оказалась равной
. Высота подъема тела оказалась равной  м. Работа силы сопротивления (в Дж) воздуха равна …
м. Работа силы сопротивления (в Дж) воздуха равна …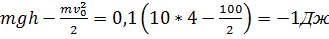 .
. зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота 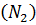 равна …
равна …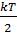 , а на каждую колебательную степень –
, а на каждую колебательную степень –  . Средняя кинетическая энергия молекулы равна
. Средняя кинетическая энергия молекулы равна 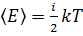 ; где
; где 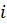 –сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней
–сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней 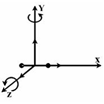 свободы равна
свободы равна  +
+  -число степеней свободы поступательного движения, равное
-число степеней свободы поступательного движения, равное  ;
;  –число степеней свободы вращательного движения, которое может быть равно
–число степеней свободы вращательного движения, которое может быть равно  Для молекулярного азота (двухатомной молекулы)
Для молекулярного азота (двухатомной молекулы) 
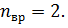 Следовательно,
Следовательно,  (3 степени свободы поступательного движения по направлениям осей ординат
(3 степени свободы поступательного движения по направлениям осей ординат 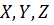 и 2 степени свободы вращательного движения вокруг осей
и 2 степени свободы вращательного движения вокруг осей 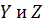 ) (см. рис.) Тогда средняя энергия молекул азота
) (см. рис.) Тогда средняя энергия молекул азота 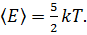
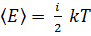 .
.  Здесь
Здесь 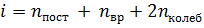 , где
, где 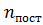 ,
,  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (He) число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (He) число i равно …  3
3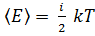 . Здесь
. Здесь 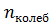 – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для азота
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для азота 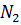 средняя кинетическая энергия колебательного движения молекулы равна …
средняя кинетическая энергия колебательного движения молекулы равна …
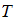 зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода (
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода ( ) равна …
) равна … 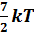
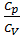 молярных теплоемкостей при постоянном давлении и постоянном объеме равно
молярных теплоемкостей при постоянном давлении и постоянном объеме равно  для …
для …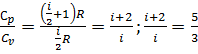 найдем
найдем 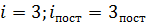 ,. Только 3 поступательные степени свободы имеют одноатомные газы, следовательно, это гелий.
,. Только 3 поступательные степени свободы имеют одноатомные газы, следовательно, это гелий.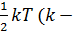 постоянная Больцмана,
постоянная Больцмана, 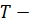 температура по шкале Кельвина). Средняя кинетическая энергия атомного водорода равна …
температура по шкале Кельвина). Средняя кинетическая энергия атомного водорода равна …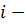 число степеней свободы молекулы. Атомарный водород –это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении
число степеней свободы молекулы. Атомарный водород –это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении  . Число степеней свободы
. Число степеней свободы  , т.к. положение центра инерции атома задается тремя координатами
, т.к. положение центра инерции атома задается тремя координатами 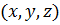 . Следовательно,
. Следовательно, 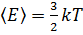 .
. №1 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении по модулю равно …
№1 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении по модулю равно …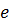 раз (
раз ( ). Работа газа (в Дж) равна …
). Работа газа (в Дж) равна …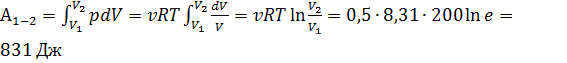
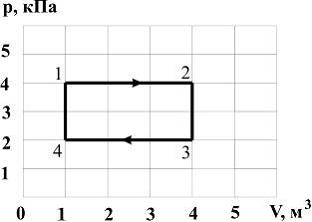 № 3 В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна
№ 3 В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна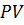 численно равна площади под графиком функции. Работа при нагревании совершается в процессе
численно равна площади под графиком функции. Работа при нагревании совершается в процессе  .
. 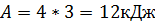 .
. №4 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна …
№4 Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна … .
. №5 На (P,V)-диаграмме изображены 2 циклических процесса.
№5 На (P,V)-диаграмме изображены 2 циклических процесса.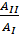 , совершенных в этих циклах, равно
, совершенных в этих циклах, равно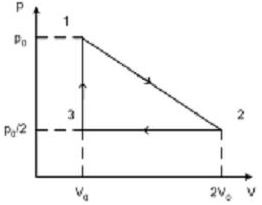 №6 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …
№6 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …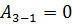 . Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.
. Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.  ; следовательно,
; следовательно,  и изменение внутренней энергии
и изменение внутренней энергии  . По
. По 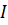 началу термодинамики для процесса 1-2 количество теплоты равно:
началу термодинамики для процесса 1-2 количество теплоты равно:  , т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.
, т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.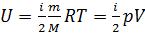 (учитываем, что
(учитываем, что 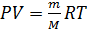 ), где
), где  давление,
давление, 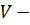 объем,
объем,  универсальная газовая постоянная,
универсальная газовая постоянная, 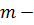 масса газа,
масса газа, 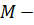
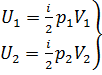 Учитывая, что
Учитывая, что  ,
, 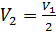 , получаем
, получаем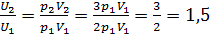 . Следовательно,
. Следовательно, 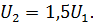
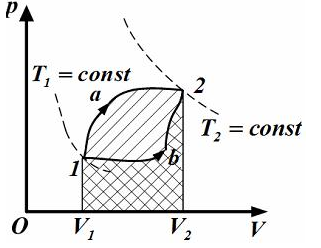
 №8 Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2),как показано на рисунке.Теплота,полученная газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями…
№8 Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2),как показано на рисунке.Теплота,полученная газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями… При этом изменение внутренней энергии,как однозначной функции термодинамического состояния системы,
При этом изменение внутренней энергии,как однозначной функции термодинамического состояния системы, 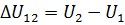 не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний:
не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний: 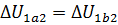 . Работа
. Работа 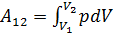 , совершаемая газом при изменение его объема от
, совершаемая газом при изменение его объема от  , зависит от процесса перехода. Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p,V(см.рис.).
, зависит от процесса перехода. Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p,V(см.рис.). 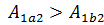 , так как площади заштрихованных фигур
, так как площади заштрихованных фигур  . Следовательно по первому закону термодинамики:
. Следовательно по первому закону термодинамики: 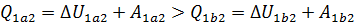 . Теплота,полученая газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями:
. Теплота,полученая газом,изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями:  .
.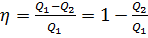 , где
, где  – количество теплоты, полученное рабочим телом от нагревателя;
– количество теплоты, полученное рабочим телом от нагревателя;  – количество теплоты, отданное рабочим телом холодильнику.
– количество теплоты, отданное рабочим телом холодильнику. 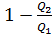 =0,8,
=0,8,  ,
, 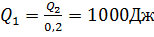 .
.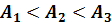 .
.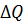 . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты 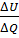 , равная …
, равная …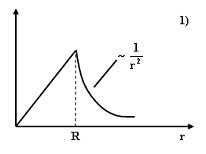


 №7 Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом
№7 Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом 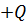 , по перемещению отрицательного заряда
, по перемещению отрицательного заряда 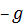 и траекторией перемещения (указаны начальная и конечная точка).
и траекторией перемещения (указаны начальная и конечная точка).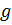 из точки 1 в точку 2 определяется по формуле:
из точки 1 в точку 2 определяется по формуле: 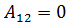 , если
, если 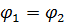 . Точки, имеющие одинаковый потенциал, лежат на одинаковом расстоянии от заряда, создающего поле
. Точки, имеющие одинаковый потенциал, лежат на одинаковом расстоянии от заряда, создающего поле  , поэтому
, поэтому 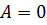 для траектории
для траектории  .
.  для траектории
для траектории 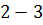 , поскольку
, поскольку  , а
, а  .
.
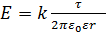 .
.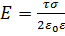 .
. ,
,  ,
, 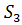 ,причем поверхность
,причем поверхность  охватывает поверхность
охватывает поверхность 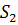 ,которая в свою очередь охватывает поверхность
,которая в свою очередь охватывает поверхность 



