
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дуализм свойств микрочастиц. Соотношение неопределенностей ГейзенбергаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
№1 Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии, равном Решение: Соотношение неопределенностей для энергии и времени имеет вид Ответ: 0,66 пэВ №2 Отношение скоростей протона и α-частицы, длины волн де Бройля которых одинаковы, равно … Решение: Длина волны де Бройля определяется формулой №3 Отношение скоростей двух микрочастиц Ответ: 1/2
№4 Отношение скоростей двух микрочастиц Ответ: 1/2 №5 Если протон и α-частица движутся с одинаковыми скоростями, то отношение длин волн де Бройля этих частиц равно … Решение: №5 Отношение неопределенностей проекций скоростей нейтрона и α-частицы на некоторое направление при условии, что соответствующие координаты частиц определены с одинаковой точностью, равно … Решение: Из соотношения неопределенностей Гейзенберга для координаты и соответствующей компоненты импульса
№6 Среднее время жизни Решение. Соотношение неопределенностей для энергии и времени имеет вид №7 В опыте Дэвиссона и Джемера исследовались дифракции прошедших ускоряющее напряжение электронов на монокристалле никеля.Если ускоряющее напряжение ументшить в 2 раза,то длина волны де Бойля электрона… Решение: Длина волны де Бойля
№8 Положение бусинки массы то для электрона неопределенность Решение: Из соотношения неопределенности Гейзенберга для координаты и соответствующей компоненты импульса
№9 Время жизни возбужденного состояния 10 нс. Учитывая, что постоянная Планка Решение: №10 Проекция скорости электрона на некоторое направление может быть найдена с неопределенностью Ответ: 11,5
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2987; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.203 (0.006 с.) |

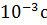 . Учитывая, что постоянная Планка
. Учитывая, что постоянная Планка  , ширина метастабильного уровня будет не менее …
, ширина метастабильного уровня будет не менее …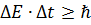 , где
, где 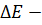 неопределенность в задании энергии (ширина энергетического уровня),
неопределенность в задании энергии (ширина энергетического уровня), 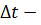 время жизни частицы в данном состоянии. Тогда
время жизни частицы в данном состоянии. Тогда 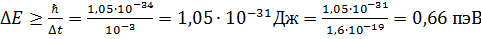
 , где h – постоянная Планка, m и v – масса и скорость частицы соответственно. Отсюда скорость частицы
, где h – постоянная Планка, m и v – масса и скорость частицы соответственно. Отсюда скорость частицы 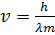 .. По условию задания
.. По условию задания 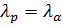 ; тогда с учетом того, что
; тогда с учетом того, что  , искомое отношение
, искомое отношение  .
.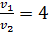 . Если их длины волн де Бройля удовлетворяют соотношению
. Если их длины волн де Бройля удовлетворяют соотношению 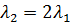 то отношение масс этих частиц
то отношение масс этих частиц  равно …
равно …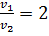 . Если их длины волн де Бройля одинаковы, то отношение масс этих частиц
. Если их длины волн де Бройля одинаковы, то отношение масс этих частиц  ..
..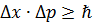 следует, что
следует, что 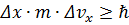 Здесь
Здесь 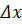 – неопределенность координаты,
– неопределенность координаты, 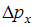 – неопределенность x-компоненты импульса,
– неопределенность x-компоненты импульса,  – неопределенность x-компоненты скорости,
– неопределенность x-компоненты скорости,  – масса частицы;
– масса частицы; 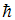 – постоянная Планка, деленная на 2π. Неопределенность x-компоненты скорости можно найти из соотношения
– постоянная Планка, деленная на 2π. Неопределенность x-компоненты скорости можно найти из соотношения 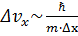 Поскольку соответствующие координаты частиц определены с одинаковой точностью, то есть
Поскольку соответствующие координаты частиц определены с одинаковой точностью, то есть  с учетом того, что
с учетом того, что 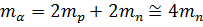 искомое отношение равно:
искомое отношение равно: 
 мезона равно
мезона равно 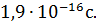 Энергетическая разрешающая способность прибора, с помощью которого можно зарегистрировать
Энергетическая разрешающая способность прибора, с помощью которого можно зарегистрировать  =
= 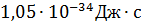 ).
).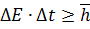 , где
, где 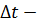 время жизни частицы в данном состоянии. Для того чтобы частицу можно было зарегистрировать с помощью измерительного прибора, его энергетическая разрешающая способность должна быть не менее
время жизни частицы в данном состоянии. Для того чтобы частицу можно было зарегистрировать с помощью измерительного прибора, его энергетическая разрешающая способность должна быть не менее 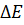 . Из соотношения неопределенностей
. Из соотношения неопределенностей 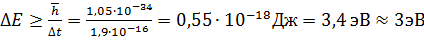
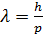 ,
, 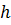 - постоянная Планка,
- постоянная Планка,  -импульс частицы. При прохождении электрон ускоряющего напряжения увеличивается его кинетическая энергия. Если считать начальную скорость электрона равной нулю,то
-импульс частицы. При прохождении электрон ускоряющего напряжения увеличивается его кинетическая энергия. Если считать начальную скорость электрона равной нулю,то  и при уменьшении ускоряющего напряжения в 2 раза длина волны де Бройля электрона
и при уменьшении ускоряющего напряжения в 2 раза длина волны де Бройля электрона 
 и положение электрона (
и положение электрона (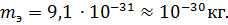 ) определены с одинаковой погрешностью.
) определены с одинаковой погрешностью. 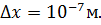 Если квантомеханическая неопределенность х-компоненты скорости бусинки составляет примерно
Если квантомеханическая неопределенность х-компоненты скорости бусинки составляет примерно  ,
,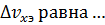
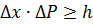 следует, что
следует, что 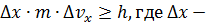 неопределенность координаты,
неопределенность координаты, неопределенность х-компоненты импульса,
неопределенность х-компоненты импульса, 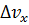 неопределенность х-компоненты скорости,m- масса частица,h- постоянная Планка, деленная на 2
неопределенность х-компоненты скорости,m- масса частица,h- постоянная Планка, деленная на 2 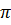 Неопределенность х-компонеты скорости можно найти из соотношения
Неопределенность х-компонеты скорости можно найти из соотношения  .Значит,для бусинки и электрона можна записать соотношение:
.Значит,для бусинки и электрона можна записать соотношение: 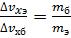 ,откуда
,откуда 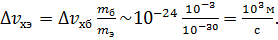
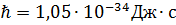 ширина энергетического уровня (в нэВ) будет не менее …
ширина энергетического уровня (в нэВ) будет не менее …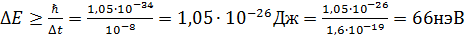
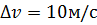 м/с. Неопределенность (в мкм) соответствующей координаты электрона не меньше …
м/с. Неопределенность (в мкм) соответствующей координаты электрона не меньше …


