
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновые свойства частиц. Соотношение неопределенностей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В 1923 году произошло примечательное событие, которое в значительной степени ускорило развитие квантовой физики. Французский физик Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики– энергия E и импульс p, а с другой стороны, волновые характеристики – круговая частота ω и длина волны λ. Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона: E = ħω, p = 2πħ/λ Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = 2πħ / p. В нерелятивистском приближении (υ << c) можно написать: λ = 2 πħ/mυ Гипотеза де Бройля основывалась на соображениях симметрии свойств материи и не имела в то время опытного подтверждения. Но она явилась мощным революционным толчком к развитию новых представлений о природе материальных объектов. В течение нескольких лет целый ряд выдающихся физиков XX века – В. Гейзенберг, Э. Шредингер, П. Дирак, Н. Бор и другие – разработали теоретические основы новой науки, которая была названа квантовой механикой. Первое экспериментальное подтверждение гипотезы де Бройля было получено в 1927 году американскими физиками К. Девиссоном и Л. Джермером. Они обнаружили, что пучок электронов, рассеивающийся на кристалле никеля, дает отчетливую дифракционную картину, подобную той, которая возникает при рассеянии на кристалле коротковолнового рентгеновского излучения. В этих экспериментах кристалл играл роль естественной дифракционной решетки. По положению дифракционных максимумов была определена длина волны электронного пучка, которая оказалась в полном соответствии с формулой де Бройля. В следующем 1928 году английский физик Дж. Томсон (сын Дж. Томсона, открывшего за 30 лет до этого электрон) получил новое подтверждение гипотезы де Бройля. В своих экспериментах Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота.
На установленной за фольгой фотопластинке отчетливо наблюдались концентрические светлые и темные кольца, радиусы которых изменялись с изменением скорости электронов (то есть длины волны) согласно де Бройлю (рис. 2).
В последующие годы опыт Дж. Томсона был многократно повторен с неизменным результатом, в том числе при условиях, когда поток электронов был настолько слабым, что через прибор единовременно могла проходить только одна частица (В. А. Фабрикант, 1948 г.). Таким образом, было экспериментально доказано, что волновые свойства присущи не только большой совокупности электронов, но и каждому электрону в отдельности. Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. Однако вследствие большой массы макроскопических тел их волновые свойства не могут быть обнаружены экспериментально. Например, пылинке массой 10–9 г, движущийся со скоростью 0,5 м/с соответствует волна де Бройля с длиной волны порядка 10–21 м, то есть приблизительно на 11 порядков меньше размеров атомов. Такая длина волны лежит за пределами доступной наблюдению области. Этот пример показывает, что макроскопические тела могут проявлять только корпускулярные свойства. Рассмотрим еще один пример. Длина волны де Бройля для электрона, ускоренного разностью потенциалов U = 100 В, может быть найдена по формуле
Это нерелятивистский случай, т. к. кинетическая энергия электрона eU = 100 эВ много меньше энергии покоя mc 2 ≈ 0,5 МэВ. Расчет дает значение λ ≈ 0,1 нм, то есть длина волны как раз оказывается порядка размеров атома. Для таких электронов кристаллическое вещество является хорошей дифракционной решеткой. Именно такие малоэнергитичные электроны дают отчетливую дифракционную картину в опытах по дифракции электронов. В то же время такой электрон, испытавший дифракционное рассеяние на кристалле как волна, взаимодействует с атомами фотопластинки как частица, вызывая почернение фотоэмульсии в какой-то определенной точке (рис. 2). Таким образом, подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни волной, ни частицей в классическом понимании. Разные свойства микрообъектов не проявляются одновременно, они дополняют друг друга, только их совокупность характеризует микрообъект полностью. В этом заключается сформулированный знаменитым датским физиком Н. Бором принцип дополнительности. Можно условно сказать, что микрообъекты распространяются как волны, а обмениваются энергией как частицы. С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большое число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля. Дифракционные явления проявляются наиболее отчетливо, когда размеры препятствия, на котором происходит дифракция вон, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты. Рассмотрим, например, дифракцию электронов на одиночной щели ширины D (рис. 3).
Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ1 этого максимума находится из условия
Это формула волновой теории. С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение py поперечного импульса равно
где p – модуль полного импульса электрона, равный, согласно де Бройлю, p = h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует
Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D. Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δpy. Таким образом, величины Δy и Δpy связаны соотношением
которое называется соотношением неопределенностей Гейзенберга. Величины Δy и Δpy нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой двигался какой-то конкретный электрон после прохождения щели и до фотопластинки в рассмотренном мысленном эксперименте. Однако, при определенных условиях соотношение неопределенностей не противоречит классическому описанию движения тел, в том числе и микрочастиц. Например, электронный пучок в кинескопе телевизора при вылете из электронной пушки имеет диаметр D порядка 10–3 см. В современном телевизоре ускоряющее напряжение U ≈ 15 кВ. Легко подсчитать импульс электрона:
Этот импульс направлен вдоль оси трубки. Из соотношения неопределенностей следует, что электронам при формировании пучка сообщается неконтролируемый импульс Δp, перпендикулярный оси пучка: Δp ≈ h / D ≈ 6,6·10–29 кг·м/с. Пусть до экрана кинескопа электроны пролетают расстояние L ≈ 0,5 м. Тогда размытие Δl пятна на экране, обусловленное волновыми свойствами электрона, составит
Поскольку Δl << D, движение электронов в кинескопе телевизора можно рассматривать с помощью законов классической механики. Таким образом, с помощью соотношения неопределенностей можно выяснить, справедливы или нет законы классической физики в тех или иных случаях. Рассмотрим еще один мысленный эксперимент – дифракцию электронного пучка на двух щелях (рис. 8.4.4). Схема этого эксперимента совпадает со схемой оптического интерференционного опыта Юнга.
Анализ этого эксперимента позволяет проиллюстрировать логические трудности, возникающие в квантовой теории. Те же проблемы возникают при объяснении оптического опыта Юнга, исходя из концепции фотонов. Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели (рис. 8.4.3). В этом случае все электроны, долетающие до фотопластинки, проходят через единственную открытую щель. Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон? Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели. Мы интуитивно представляем себе поток микрочастиц как направленное движение маленьких шариков и применяем для описания этого движения законы классической физики. Но электрон (и любая другая микрочастица) обладает не только корпускулярными, но и волновыми свойствами. Легко представить, как электромагнитная световая волна проходит через две щели в оптическом опыте Юнга, т. к. волна не локализована в пространстве. Но если принять концепцию фотонов, то мы должны признать, что каждый фотон тоже не локализован. Невозможно указать, через какую из щелей пролетел фотон, как невозможно проследить за траекторией движения фотона до фотопластинки и указать точку, в которую он попадет. Опыт показывает, что даже в том случае, когда фотоны пролетают через интерферометр поштучно, интерференционная картина после пролета многих независимых фотонов все равно возникает. Поэтому в квантовой физике делается вывод: фотон интерферирует сам с собой. Все вышесказанное относится и к опыту по дифракции электронов на двух щелях. Вся совокупность известных экспериментальных фактов может найти объяснение, если принять, что дебройлевская волна каждого отдельного электрона проходит одновременно через оба отверстия, в результате чего и возникает интерференция. Поштучный поток электронов тоже дает интерференцию при длительной экспозиции, то есть электрон, как и фотон, интерферирует сам с собой. Рассмотрение стационарных задач квантовой механики начнем с наиболее простой для анализа задачи – о движении частицы в потенциальной яме с непроницаемыми, т.е. бесконечно высокими стенками. Рассмотрим частицу, находящуюся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. В этом случае потенциальная энергия частицы имеет вид U(x)
т.е. внутри ямы (0< x<a) потенциальная энергия U(x) постоянна и равна нулю, а вне ямы обращается в бесконечность (рис.4.1).
Запишем уравнение Шредингера для одномерного движения частицы вдоль оси x:
Поскольку вне ямы потенциальная энергия обращается в бесконечность, то для того, чтобы выполнялось уравнение (1), необходимо, чтобы вне ямы волновая функция ψ(x) обращалась в ноль, т.е. ψ(x)≡ 0. Это означает, что в случае ямы с бесконечно высокими стенками частица не может выйти за пределы ямы, поскольку такие стенки являются непроницаемыми для частицы. В силу непрерывности волновая функция ψ(x) должна обращаться в нуль и на границах ямы: при и при x = 0 и x = a. Таким образом, задача о движении частицы в яме сводится к решению уравнения
с граничными условиями
Введем обозначение
При этом уравнение (2) принимает вид хорошо известного из теории колебаний уравнения
Общее решение которого, есть
Используя граничное условие
откуда следует, что
а при нечетных значениях m
Однако, физический смысл имеет не сама волновая функция ψ(x), а квадрат ее модуля Второе граничное условие
которое для
Отметим, что значение n= 0, формально также входящее в решение (4), не удовлетворяет условию задачи, т.к. при этом ψ(x)≡ 0, что означает, что частица в яме отсутствует. Поэтому значение n= 0 следует отбросить. Подставляя (5) в (3), приходим к выражению для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками
Важной особенностью полученного энергетического спектра (6) является его дискретность. Частица, находящаяся в потенциальной яме, может иметь только дискретные, квантованные, значения энергии, определяемые выражением (6) (см.рис.4.2). Отметим, что решение
уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы. Число n в (6), определяющее энергию частицы в яме, называется квантовым числом, а соответствующее ему значение En – уровнем энергии. Состояние частицы с наименьшей энергией, в данном случае с n= 1, называется основным состоянием. Все остальные состояния являются возбужденными: значение n= 2 отвечает первому возбужденному состоянию, значение n= 3 – второму возбужденному состоянию и т.д. Следует отметить, что минимальное значение энергии частицы, находящейся в основном состоянии, отлично от нуля. Этот результат согласуется с соотношением неопределенностей и является общим для всех задач квантовой механики. В классической механике минимальную энергию, равную нулю, имеет покоящаяся в яме частица. Такого состояния покоя у квантовой частицы не существует. Обсудим подробнее вопрос о дискретности энергетического спектра. Разность энергий n -го и (n+ 1)-го энергетических уровней ΔEn равна
Оценим величину ΔEn для конкретных случаев. Случай 1. Рассмотрим молекулу газа массой m 0 ≈ 10-27кг в сосуде размером a ≈ 0,1м. При этом
ΔEn ≈ 6,8·10-20· n эВ.
Энергетическое расстояние между соседними уровнями оказывается столь малым по сравнению с энергией теплового хаотического движения молекулы kT (при комнатной температуре kT ≈ 2,6·10-2 эВ), что практически можно говорить о сплошном энергетическом спектре движущейся молекулы. Случай 2. Рассмотрим свободный электрон в атоме (a ≈ 10-10 м). При этом разность энергий соседних уровней равна ΔEn ≈ 0,75·102· n эВ.
Это заметная величина по сравнению, например, с энергией связи электрона в атоме (Eсв ~ 10 эВ). Поэтому дискретность энергетического спектра в этом случае оказывается весьма существенной. Завершая обсуждение энергетического спектра частицы в потенциальной яме (6), отметим еще одно его свойство. Рассмотрим отношение
При увеличении квантового числа n это отношение уменьшается, таким образом, дискретность энергетического спектра с возрастанием n играет все меньшую роль. Данный результат представляет собой проявление важного физического принципа – принципа соответствия, согласно которому при больших значениях квантового числа n, т.е. при Перейдем теперь к анализу волновых функций частицы, находящейся в одномерной потенциальной яме. Из (4) с учетом (5) получаем
Множитель A находится из условия нормировки волновой функции (7):
Таким образом, для A получаем
и волновые функции частицы в одномерной потенциальной яме с бесконечно высокими стенками имеют вид
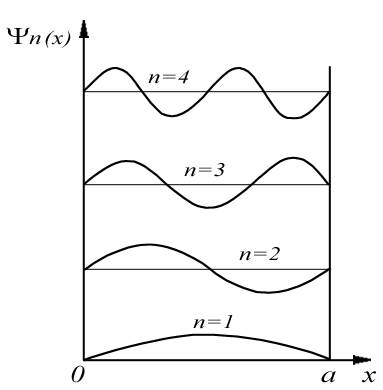
Графики волновых функций ψn(x) для первых четырех значений квантового числа n приведены на рис.4.3. Волновые функции, отвечающие разным значениям n, существенно отличаются друг от друга. Если поместить начало координат в середину ямы, то волновые функции частицы внутри ямы для нечетных значений n будут четными функциями координаты x, и наоборот, волновые функции для четных n - нечетными функциями координаты. При увеличении квантового числа n на единицу число точек пересечения волновой функции с осью x также увеличивается на единицу. Отличительным свойством найденных волновых функций является излом, т.е. скачок производной на границах ямы. Этот скачок возникает вследствие того, что на границах ямы потенциальная энергия частицы U(x) обращается в бесконечность. В случае ямы конечной глубины, скачок производной волновой функции на границе ямы отсутствует, т.е. волновая функция является гладкой. На рис.4.4 представлены графики квадрата модуля волновой функции
Плотность вероятности оказывается существенно различной для разных состояний частицы, т.е. для разных значений квантового числа n. Так, например, в основном состоянии, т.е. при n = 1, частица с наибольшей вероятностью находится в центре ямы, а в первом возбужденном состоянии, т.е. при n = 2, вероятность обнаружить частицу в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно. Такое поведение кардинально отличается от поведения в яме классической частицы, для которой плотность вероятности нахождения частицы одинакова в любой точке ямы. Вероятность того, что частица в яме находится в области
Отметим, что с математической точки зрения задача о движении частицы в одномерной потенциальной яме с непроницаемыми стенками аналогична задаче о колебании струны с закрепленными концами. И в том, и в другом случае из граничных условий следует, что на ширине ямы (на длине струны) должно укладываться целое число полуволн Лазеры
Лазеры или оптические квантовые генераторы – это современные когерентные источники излучения, обладающие целым рядом уникальных свойств. Создание лазеров явилось одним из самых замечательных достижений физики второй половины XX века, которое привело к революционным изменениям во многих областях науки и техники. К настоящему времени создано большое количество лазеров с различными характеристиками – газовых, твердотельных, полупроводниковых, излучающих свет в различных оптических диапазонах. Лазеры могут работать в импульсном и непрерывном режимах. Мощность излучения лазеров может изменяться в пределах от долей милливатта до 1012–1013 Вт (в импульсном режиме). Лазеры находят широкое применение в военной технике, в технологии обработки материалов, в медицине, в оптических системах навигации, связи и локации, в прецизионных интерференционных экспериментах, в химии, просто в быту и т. д. Хотя первый лазер был построен сравнительно недавно (1960 г.), современную жизнь уже невозможно представить без лазеров. Одним из важнейших свойств лазерного излучения является чрезвычайно высокая степень его монохроматичности, недостижимая в излучении нелазерных источников. Это и все другие уникальные свойства лазерного излучения возникают в результате согласованного, кооперативного испускания световых квантов многими атомами рабочего вещества. Чтобы понять принцип работы лазера, нужно более внимательно изучить процессы поглощения и излучения атомами квантов света. Атом может находиться в различных энергетических состояниях с энергиями E 1, E 2 и т. д. В теории Бора эти состояния называются стабильными. На самом деле стабильным состоянием, в котором атом может находиться бесконечно долго в отсутствие внешних возмущений, является только состояние с наименьшей энергией. Это состояние называют основным. Все другие состояния нестабильны. Возбужденный атом может пребывать в этих состояниях лишь очень короткое время, порядка 10–8 с, после этого он самопроизвольно переходит в одно из низших состояний, испуская квант света, частоту которого можно определить из второго постулата Бора. Излучение, испускаемое при самопроизвольном переходе атома из одного состояния в другое, называют спонтанным. На некоторых энергетических уровнях атом может пребывать значительно большее время, порядка 10–3 с. Такие уровни называются метастабильными. Переход атома в более высокое энергетическое состояние может происходить при резонансном поглощении фотона, энергия которого равна разности энергий атома в конечном и начальном состояниях. Переходы между энергетическими уровнями атома не обязательно связаны с поглощением или испусканием фотонов. Атом может приобрести или отдать часть своей энергии и перейти в другое квантовое состояние в результате взаимодействия с другими атомами или столкновений с электронами. Такие переходы называются безизлучательными. Теперь самое главное. В 1916 году А. Эйнштейн предсказал, что переход электрона в атоме с верхнего энергетического уровня на нижний может происходить под влиянием внешнего электромагнитного поля, частота которого равна собственной частоте перехода. Возникающее при этом излучение называют вынужденным или индуцированным. Вынужденное излучение обладает удивительным свойством. Оно резко отличается от спонтанного излучения. В результате взаимодействия возбужденного атома с фотоном атом испускает еще один фотон той же самой частоты, распространяющийся в том же направлении. На языке волновой теории это означает, что атом излучает электромагнитную волну, у которой частота, фаза, поляризация и направление распространения точно такие же, как и у первоначальной волны. В результате вынужденного испускания фотонов амплитуда волны, распространяющейся в среде, возрастает. С точки зрения квантовой теории, в результате взаимодействия возбужденного атома с фотоном, частота которого равна частоте перехода, появляются два совершенно одинаковых фотона-близнеца. Именно индуцированное излучение является физической основой работы лазеров. На рис. 9.4.1 схематически представлены возможные механизмы переходов между двумя энергетическими состояниями атома с поглощением или испусканием кванта.
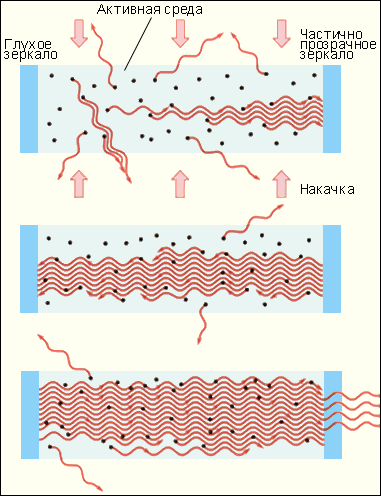
Рассмотрим слой прозрачного вещества, атомы которого могут находиться в состояниях с энергиями E 1 и E 2 > E 1. Пусть в этом слое распространяется излучение резонансной частоты перехода ν = ΔE / h. Согласно распределению Больцмана, при термодинамическом равновесии большее количество атомов вещества будет находиться в нижнем энергетическом состоянии. Некоторая часть атомов будет находиться и в верхнем энергетическом состоянии, получая необходимую энергию при столкновениях с другими атомами. Обозначим населенности нижнего и верхнего уровней соответственно через n 1 и n 2 < n 1. При распространении резонансного излучения в такой среде будут происходить все три процесса, изображенные на рис. 1. Эйнштейн показал, что процесс (a) поглощения фотона невозбужденным атомом и процесс (c) индуцированного испускания кванта возбужденным атомом имеют одинаковые вероятности. Так как n 2 < n 1 поглощение фотонов будет происходить чаще, чем индуцированное испускание. В результате прошедшее через слой вещества излучение будет ослабляться. Это явление напоминает появление темных фраунгоферовских линий в спектре солнечного излучения. Излучение, возникающее в результате спонтанных переходов, некогерентно и распространяется во всевозможных направлениях и не дает вклада в проходящую волну. Чтобы проходящая через слой вещества волна усиливалась, нужно искусственно создать условия, при которых n 2 > n 1, то есть создать инверсную населенность уровней. Такая среда является термодинамически неравновесной. Идея использования неравновесных сред для получения оптического усиления впервые была высказана В. А. Фабрикантом в 1940 году. В 1954 году советские физики Н. Г. Басов и А. М. Прохоров и независимо от них американский ученый Ч. Таунс использовали явление индуцированного испускания для создания микроволнового генератора радиоволн с длиной волны λ = 1,27 см. За разработку нового принципа усиления и генерации радиоволн в 1964 году все трое были удостоены Нобелевской премии. Среда, в которой создана инверсная населенность уровней, называется активной. Она может служить резонансным усилителем светового сигнала. Для того, чтобы возникала генерация света, необходимо использовать обратную связь. Для этого активную среду нужно расположить между двумя высококачественными зеркалами, отражающими свет строго назад, чтобы он многократно прошел через активную среду, вызывая лавинообразный процесс индуцированной эмиссии когерентных фотонов. При этом в среде должна поддерживаться инверсная населенность уровней. Этот процесс в лазерной физике принято называть накачкой. Начало лавинообразному процессу в такой системе при определенных условиях может положить случайный спонтанный акт, при котором возникает излучение, направленное вдоль оси системы. Через некоторое время в такой системе возникает стационарный режим генерации. Это и есть лазер. Лазерное излучение выводится наружу через одно (или оба) из зеркал, обладающее частичной прозрачностью. На рис. 2 схематически представлено развитие лавинообразного процесса в лазере.
Существуют различные способы получения среды с инверсной населенностью уровней. В рубиновом лазере используется оптическая накачка. Атомы возбуждаются за счет поглощения света. Но для этого недостаточно только двух уровней. Каким бы мощным не был свет лампы–накачки, число возбужденных атомов не будет больше числа невозбужденных. В рубиновом лазере накачка производится через третий выше расположенный уровень (рис. 3).
После вспышки мощной лампы, расположенной рядом с рубиновым стержнем, многие атомы хрома, входящего в виде примеси в кристалл рубина (около 0,05 %), переходят в состояние с энергией E 3, а через промежуток τ ≈ 10–8 с они переходят в состояние с энергией E 2. Перенаселенность возбужденного уровня E 2 по сравнению с невозбужденным уровнем E 1 возникает из-за относительно большого времени жизни уровня E 2. Лазер на рубине работает в импульсном режиме на длине волны 694 мм (темно-вишневый свет), мощность излучения может достигать в импульсе 106–109 Вт. Исторически это был первый действующий лазер (американский физик Т. Майман, 1960 г.). Одним из самых распространенных лазеров в настоящее время является газовый лазер на смеси гелия и неона. Общее давление в смеси составляет порядка 102 Па при соотношении компонент He и Ne примерно 10: 1. Активным газом, на котором возникает генерация на длине волны 632,8 нм (ярко-красный свет) в непрерывном режиме, является неон. Гелий является буферным газом, он участвует в механизме создания инверсной населенности одного из верхних уровней неона. Излучение He–Ne лазера обладает исключительной, непревзойденной монохроматичностью. Расчеты показывают, что спектральная ширина линии генерации He–Ne лазера составляет примерно Δν ≈ 5·10–4 Гц. Это фантастически малая величина. Время когерентности такого излучения оказывается порядка τ ≈ 1 / Δν ≈ 2·103 с, а длина когерентности cτ ≈ 6·1011 м, то есть больше диаметра земной орбиты! На практике многие технические причины мешают реализовать столь узкую спектральную линию He–Ne лазера. Путем тщательной стабилизации всех параметров лазерной установки удается достичь относительной ширины Δν / ν порядка 10–14–10–15, что примерно на 3–4 порядка хуже теоретического предела. Но и реально достигнутая монохроматичность излучения He–Ne лазера делает этот прибор совершенно незаменимым при решении многих научных и технических задач. Первый гелий-неоновый лазер был создан в 1961 году. На рис.4 представлена упрощенная схема уровней гелия и неона и механизм создания инверсной населенности лазерного перехода.
Накачка лазерного перехода E 4 → E 3 в неоне осуществляется следующим образом. В высоковольтном электрическом разряде вследствие соударений с электронами значительная часть атомов гелия переходит в верхнее метастабильное состояния E 2. Возбужденные атомы гелия неупруго сталкиваются с атомами неона, находящимися в основном состояние, и передают им свою энергию. Уровень E 4 неона расположен на 0,05 эВ выше метастабильного уровня E 2 гелия. Недостаток энергии компенсируется за счет кинетической энергии соударяющихся атомов. На уровне E 4 неона возникает инверсная населенность по отношению к уровню E 3, который сильно обедняется за счет спонтанных переходов на ниже расположенные уровни. При достаточно высоком уровне накачки в смеси гелия и неона начинается лавинообразный процесс размножения идентичных когерентных фотонов. Если кювета со смесью газов помещена между высокоотражающими зеркалами, то возникает лазерная генерация. На рис. 5 изо
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.016 с.) |




 3
3


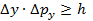 ,
,

 4
4
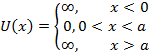
 Рисунок 13
Рисунок 13






 , получаем
, получаем
 , где m = 0,1,2,…. Отметим, что при четных значениях m и при m = 0
, где m = 0,1,2,…. Отметим, что при четных значениях m и при m = 0 ,
, .
. , который от выбора значения m, т.е. от знака ψ(x) не зависит. Поэтому без потери общности можно считать, что α= 0.
, который от выбора значения m, т.е. от знака ψ(x) не зависит. Поэтому без потери общности можно считать, что α= 0. приводит к соотношению
приводит к соотношению
 выполняется при
выполняется при



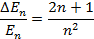
 , квантовая механика переходит в механику классическую.
, квантовая механика переходит в механику классическую.

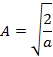

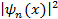 , определяющего плотность вероятности нахождения частицы в яме.
, определяющего плотность вероятности нахождения частицы в яме. Рисунок 16
Рисунок 16
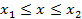 , определяется выражением
, определяется выражением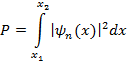
 . В нашем случае λ - это дебройлевская длина волны частицы в яме.
. В нашем случае λ - это дебройлевская длина волны частицы в яме. 1
1
 2
2
 3
3
 4
4



