
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальная теория относительности.Содержание книги Поиск на нашем сайте
В классической физике до появления теории относительности (1905 г.), предполагалось, что любой физический процесс, использованный (как «эталонный») для измерения времени, выявляет одно и то же течение «мирового» или абсолютного времени. Предполагалось также, что течение времени, измеренное при помощи любых часов, не зависит от того, покоятся или движутся эти часы относительно данной системы отсчета. А. Эйнштейн прежде всего указал на недостаточную обоснованность этих предположений и на необходимость предварительного выбора строго определенного (однозначного) способа измерения времени, пригодного (без изменений) для всех условий, в которых производятся эти измерения. Для того чтобы более отчетливо изложить его физические идеи, рассмотрим подробнее способы измерения длин, расстояний и времени. Допустим, что нам необходимо измерить расстояние между точками А и В, отмеченными на каком-нибудь твердом предмете. Измерения будем относить к системе отсчета S, связанной с поверхностью Земли. Вначале предположим, что предмет покоится относительно Земли. Для производства измерения необходимо прежде всего выбрать эталон длины (например, металлическая линейка), а затем указать, какие операции необходимо произвести с этим эталоном, чтобы получить результат измерения (перекладывание эталона вдоль измеряемой длины). Если эталоном является длина световой волны, то необходимо указать, каким образом должно быть произведено сравнение измеряемой длины с длиной световой волны; для этой цели, очевидно, понадобятся соответствующие приборы, например — интерферометры. Однако каждый «способ измерения» должен содержать в себе указание о том, как следует измерять данную физическую величину во всех условиях, в которых приходится производить измерение. В частности, приходится измерять размеры не только покоящихся (относительно системы отсчета), но и движущихся тел. В этой весьма важной части «способа измерения» возможны два приема: 1) можно каждый раз сообщить измерительному прибору (например, эталону длины или интерферометру) такие же скорости, какие имеет измеряемый предмет. В этом случае измерительный прибор в процессе измерений всегда покоится относительно предмета, но движется относительно системы отсчета. Нам необходимо знать, не изменяется ли эталон длины вследствие своего движения и не зависят ли результаты измерения от скорости этого движения; 2) можно отметить те точки A' и B' системы отсчета, в которых одновременно находятся точки А и В движущегося предмета, и затем определить расстояние между А' и В'. В этом случае измерительный прибор в процессе его использования всегда покоится относительно системы отсчета. Это удобно, но оно связано с необходимостью дополнительно измерять время, так как одновременность совпадения точек А и А', В и В' должна быть отмечена по часам. Поэтому, если имеется однозначный способ измерения времени (а следовательно, способ установления одновременности совпадений точек А и А', В и В'), то второй прием будет иметь преимущество перед первым. Заметим, что оба приема не применимы, если необходимо измерять расстояние между двумя точками пространства, например, атомного или космического масштаба. Расстояние, не фиксированное твердыми телами, не может быть измерено эталонными линейками. Поэтому это расстояние либо вообще не может быть основной величиной (т. е. величиной, для которой выбран эталон), либо же для него должен быть указан новый способ измерения, который необходимо отдельно проанализировать, чтобы выявить все содержащие в нем предположения. Рассмотрим измерение времени; для этого необходимо выбрать часы, т. е. физические системы, в которых происходит какой-нибудь периодический процесс. Результатом измерения времени в данном месте является подсчет числа возвращений часов и одно и то же фиксируемое состояние. Для измерения времени в различных местах возможны два приема: 1) можно изготовить некоторое множество совершенно одинаковых часов, отрегулировать их ход в определенном месте (и при определенной ориентировке их осей) и затем расставить их в интересующих нас местах, где должно производиться измерение времени. При этом необходимо знать, не изменяется ли ход часов при их переносе и работают ли они синхронно в местах назначения. Вполне возможно, что, например, в различных местах поля тяготения Земли часы имеют различный ход; 2) можно предварительно расставить эти часы и затем уже согласовать их ход между собой при помощи каких-нибудь «сигналов времени» — световых вспышек и т. д. В этом случае необходимо заранее знать законы распространения сигналов в данной системе отсчета. Для измерения времени в движущихся физических системах можно, опять-таки, либо пользоваться часами, которые движутся вместе с системой и, следовательно, неподвижны относительно нее (в этом случае нужно знать, как зависит ход часов от скорости их движения); либо же пользоваться «сигналами времени» (в этом случае необходимо знать законы распространения этих сигналов относительно любой физической системы, в которой производится измерение времени). Нет уверенности в том, что результаты измерения времени при помощи всех этих способов будут совпадать. Таким образом, при рассмотрении способов измерения физических величин, в частности — длины и времени, обнаруживается следующая проблема: при производстве измерений необходимо заранее знать, как изменяются измерительные приборы и, в частности, эталоны физических величин (линейка, часы и т. п.) в процессе измерений. Сами результаты измерений — число перекладываний линейки или подсчет числа колебаний в часах и т. д. — не могут решить этой проблемы. Можно было бы выяснить поведение эталонов в различных условиях их применения, если были бы известны необходимые для этого законы физики, но они могут быть установлены только после производства и обработки измерений; заранее они не могут быть известны. Особенно отчетливо выявляется возникающее здесь затруднение при измерении времени при помощи «сигналов», например, световых вспышек. Для измерения времени, прошедшего с момента выхода сигнала из одной точки до момента прихода сигнала в другую точку, должны быть заранее известны законы распространения света, но эти законы могут быть получены только после экспериментального изучения распространения света, для чего способ измерения времени уже должен быть выбран. Очевидно, указанную выше проблему можно разрешить, если удастся найти такие законы физики, установление которых не требует производства измерений. Тогда способы измерения физических величин могли быть основаны на таких законах; остальные законы физики получатся в результате обработки измерений. Таким (не зависящим от способов измерения физических величин) законом физики является следующий результат: движение физических систем относительно пространства («мирового эфира») не обнаруживается. Такого рода движение являлось бы абсолютным движением. Обсудим это подробнее. Допустим, что пассажир смотрит из окна своего поезда па проходящий мимо него другой поезд. Если при этом поезд движется равномерно и в поле зрения нет никаких ориентиров, то пассажиру не удастся установить, что же в действительности движется: его собственный или тот, другой поезд, а может быть, оба поезда. Эго знакомый всем опыт. Относительную скорость двух поездов можно измерить легко, но, чтобы определить то, что мы называем истинной скоростью поезда, необходимо хотя бы мельком взглянуть на землю, которая послужит системой отсчета для измерения скорости. Теперь предположим, что два воздушных шара движутся друг относительно друга над облаками. Наблюдателю на одном из шаров будет казаться, что сам он стоит на месте, а движется другой шар. Получив данные наблюдений с Земли, он сможет вычислить лишь свою скорость по отношению к Земле. Астроном мог бы продолжить эту работу, сообщив ему скорость данной точки Земли относительно Солнца, а затем скорость Солнца по отношению одной из «неподвижных звезд». Однако и это все не поможет наблюдателю определить его действительную, или абсолютную, скорость. Есть ли основание считать какие-либо звезды неподвижными? Ведь известно, что звезды также движутся друг относительно друга. Какой смысл вообще имеет в действительности слово «неподвижный»? Есть ли что-либо во Вселенной, что можно было бы считать неподвижным? Ученым не по душе представление о том, что все измерения, относящиеся к движению, должны быть относительными. Это как бы свидетельствует о том, что сооружение, олицетворяющее механику Вселенной, выстроено на зыбком фундаменте. Поэтому в тот момент, когда физикам потребовалась среда, заполняющая все пространство, на сцене появился эфир, и не только как действующее лицо в теории света и электричества, по и как стандартная система отсчета для измерения абсолютной скорости. Ученые же приступили к измерению скорости Земли относительно эфира. В 1887 г. Майкельсон и Морли поставили классический опыт, который имел отношение к этой проблеме и который можно взять в качестве исходного пункта для изложения специальной теории относительности Эйнштейна. Идею этого опыта легко уяснить на следующей аналогии. Пусть скорость воды в реке с прямолинейными параллельными берегами, отстоящими друг от друга на 90 м, составляет 4 м/сек. Двое гребцов отправляются из пункта А на одном берегу, причем один Т направляется поперек реки к противоположному берегу в пункт В, а другой L, кпункту С, расположенному на 90 м ниже по течению, а затем обратно в А. Каждый гребет со скоростью 5 м/сек по отношению воды. Сравните время, затраченное каждым из них.
Аналогично на обратный путь из В в А потребуется еще 30 сек, так что весь путь в оба конца займет 60 сек. Гребец L, плывя к пункту С, движется относительно воды со скоростью 5 м/сск, течение сносит его ежесекундно еще на 4 м. Таким образом, он делает ежесекундно 9 м. Время, которое потребуется для того, чтобы попасть из пункта А в пункт С, равно 90/9=10 сек. Однако, возвращаясь из С против течения, гребец будет делать всего 5 - 4= 1 м/сек. Следовательно, из С в А он будет плыть 90/1=90 сек, а полное время вниз и вверх по течению составит 10 + 90 = = 100 сек. Отношение времени, которое потребуется гребцу L, ко времени, которое затратит гребец Т, равно 100/60 = 5/3. Таким образом, плавание вверх и вниз по течению связано с затратой большего времени, нежели плавание на такое же расстояние поперек течения. Разбор этого примера показывает также, что если известно отношение промежутков времени, занимаемых поездкой на равное расстояние в двух направлениях, то это позволяет вычислить скорость течения реки. Из опыта известно, что свет всегда распространяется в эфире с постоянной скоростью 300000 км/сек. Предположим, что в определенный момент Земля движется в эфире скоростью и км/сек в направлении от С к А. С точки зрения земного наблюдателя, эфир проносится мимо точки А в направлении от А к С со скоростью и км/сек. Допустим, что к концам двух жестких перпендикулярных друг другу стержней АС и АВ прикреплены зеркала, обращенны Итак, чтобы проплыть любое заданное расстояние вверх и вниз по течению, требуется больше времени, чем на то же расстояние поперек течения и обратно. Следовательно, сигнал из точки С должен вернуться в А позже сигнала, посланного в точку В. Если затем вычислить отношение промежутков времени, затраченного обоими сигналами, то это позволит оцепить скорость эфира и равную но величине и противоположную по направлению скорость Земли в эфире. Опыт Майкельсона — Морли должен был измерить отношение этих промежутков времени. Детальное описание использованного в этом опыте прибора можно найти в любом учебнике по оптике. К удивлению экспериментаторов, в этом состязании не оказалось победителя: оба сигнала вернулись в А одновременно. Так как Земли движется по своей орбите вокруг Солнца со скоростью приблизительно 30 км/сек, то в моменты времени, отстоящие друг от друга на 6 месяцев, разница в скоростях относительно эфира составит 60 км/сек. Следовательно, если бы Земля оказалась в один из моментов времени покоящейся относительно эфира, то этого уже не могло случиться полгода спустя. Однако повторение опыта через 6 месяцев по-прежнему не дало никакого результата. Чтобы исключить возможные ошибки, связанные с различием длин плеч прибора АВ и АС, опыт был повторен с поворотом плеч так, что направление АВ совпало с предполагаемым направлением потока, а направление АС оказалось перпендикулярным ему. Но и в этом случае не удалось обнаружить никакой разницы. В дальнейшем в качестве АВ были испробованы различные направления, и снова безрезультатно. Позднее эксперимент повторялся с усовершенствованной методикой, позволявшей. малые скорости до 0.2 км/сек. И в этом случае был получен результат, противоречивший выводам теории. Стало ясно, что в теории что-то неблагополучно. Ученые оказались вынужденными искать объяснение или модификацию теории, которые позволили бы согласовать расчеты с результатами наблюдений. Вернемся к примеру с лодками, которые аналогичны световым сигналам в опыте Майкельсона — Морли. В этом случае обе лодки отправятся одновременно и, ко всеобщему изумлению, одновременно возвратятся. Как можно совместить подобный результат с выводами, полученными с помощью выкладок? Первое предположение заключается в том, что L гребет быстрее (относительно воды), нежели T; однако его следует отбросить, ибо этой скорости в опыте Майкельсона — Морли соответствует скорость распространения свела в эфире, которая, как мы знаем, постоянна и равна 300 000 км/сек. Следующее предположение заключается в неравенстве путей: длина АС может оказаться меньше длины АВ из-за небрежности измерения. Однако оно несостоятельно, так как в опыте Майкельсона — Морли перемена местами жестких плеч АС и АВ по-прежнему не приводила к появлению разницы во времени. Затем Фитцджеральд предположил, что неравенство плеч АВ и АС связано не с ошибкой в измерении расстояния, а с автоматическим сокращением длины стержня при его перемещении из положения, перпендикулярного течению, в положение вдоль течения. Подобное сокращение нельзя обнаружить с помощью измерений, поскольку линейка, которой измеряется длина плеча АС, сокращается в той же самой пропорции, что и плечо. Это гипотетическое явление носит название «фитцджеральдово сокращение». Величина его, конечно, зависит от скорости течения. Если скорость течения составляет 4 м/сек, а скорость лодки 5 м/сек, то коэффициент сжатия оказывается равным Эйнштейн выдвинул два общих принципа, или аксиомы: 1. Равномерное движение через эфир не поддается обнаружению. 2. При любом волновом процессе скорость распространения полны не зависит от скорости источника. Остановимся на смысле этих аксиом. Измерить скорость одного тела по отношению другого не представляет труда. Все наши представления о скорости по существу являются представлениями об относительной скорости: речь идет либо о скоростях различных предметов относительно нас самих, либо о нашей собственной скорости по отношении) к чему-либо еще. Например, водитель, глядя на дорогу, по которой он ведет машину, по всей вероятности, оценивает свою собственную скорость относительно дороги. Но бессмысленно ставить вопрос о скорости относительно эфира, ибо нет никакой возможности отличить один участок эфира от другого. Можно опознать вещество, находящееся в эфире, но сам эфир не поддается отождествлению. И поскольку эфир, образно выражаясь, нельзя разметить верстовыми столбами, то утверждение, что тело движется через эфир, не содержит никакой информации о движении, или, иными словами, не имеет смысла по отношению эфира. Смысл второй аксиомы, по-видимому, более прозрачен. Представим себе паровоз, идущий по прямолинейному участку пути с постоянной скоростью в совершенно тихую погоду. Если машинист бросит вперед камень, то человек, стоящий у железнодорожного полотна, увидит, что скорость камня равна скорости, которую ему сообщил машинист, плюс скорость паровоза. Чем быстрей идет поезд, тем быстрей будет двигаться камень, хотя усилие машиниста останется прежним. Таким образом, скорость камня в воздухе зависит от скорости источника, в данном случае машиниста. Допустим, что паровоз дает гудок, который слышен человеку, оставшемуся далеко позади. Мы знаем, что звук распространяется в воздухе в виде волн со скоростью примерно 340 м/сек. Движение звуковой волны не похоже на движение камня: скорость распространения звука в воздухе не зависит от скорости паровоза в момент, когда дается гудок, т. е. не зависит от скорости источника. Скорость поезда повлияет на высоту звука, т. е. на музыкальный тон. Однако время, через которое волна достигнет наблюдателя, не зависит от скорости движения паровоза. Если теперь движущееся тело испускает свет, то скорость распространения световых волн в эфире никак не будет связана со скоростью тела. Можно было ожидать, что движение тел относительно «мирового эфира» повлияет на форму и размеры тел, на распределение зарядов в них, на форму эквипотенциальных поверхностей силовых полей (электрических, гравитационных), на форму волновых поверхностей света, испускаемого телами, и т. д. Большая группа экспериментов была поставлена с целью обнаружить влияние орбитального движения Земли на свойства тел или на течение физических процессов. Например, расчеты показывали, что при повороте интерферометра Майкельсона должно было наблюдаться заметное смещение интерференционных полос, пропорциональное скорости движения этого прибора вместе с Землей; однако это смещение не было обнаружено. При измерении сопротивления прямолинейного проводника (например, при помощи мостика Уитстона) ориентировали его по направлению движения Земли и перпендикулярно к этому направлению; ожидаемое изменение сопротивления также не было обнаружено. На основании многочисленных подобных экспериментов было установлено, что направление и скорость движения тел относительно «мирового эфира» обнаружить невозможно. Среди других законов физики этот экспериментально установленный результат выделяется тем, что он не связан с производством каких-либо измерений, в которых было бы необходимо употребление эталонов или других измерительных приборов. Действительно, для того чтобы показать, что движение физических систем, установленных на Земле, относительно «мирового эфира» обнаружить невозможно, нужно только констатировать отсутствие регистрируемых изменений в экспериментальных установках при их повороте. Например, чтобы отметить отсутствие интерференционного эффекта в приборе Майкельсона при его поворотах, вовсе нет необходимости измерять расстояния до зеркал или время распространения света в различных направлениях. Точно так же и в других экспериментах фиксируется только отсутствие ожидаемого эффекта при движении измерительной установки относительно «мирового эфира»; никаких измерений производить не приходится, поэтому в предварительном выборе способов измерения физических величин нет необходимости. Окружающее нас пространство («мировой эфир»} играет исключительную роль в физических явлениях; в нем существуют гравитационные, электрические, магнитные поля, распространяются электромагнитные волны, через него осуществляются всевозможные взаимодействия между телами и т. д. Поэтому, если движение тел относительно «мирового эфира» не обнаруживается, то это означает, что наблюдаемые нами физические явления происходят совершенно одинаково в системах покоящихся или как угодно движущихся относительно мирового эфира. Из этого утверждения можно сделать вывод, что законы физики должны иметь одинаковый вид по отношению к различным системам отсчета. В частности, если измерение времени производится при помощи «сигналов», то закон распространения этих сигналов можно выбрать одинаковым для всех систем отсчета. Эти результаты были использованы А. Эйнштейном в разработанной им теории относительности. В первой части этой теории — в так называемой специальной теории относительности — утверждается следующее: 1) законы физических явлений имеют одинаковый вид по отношению ко всем инерциальным системам отсчета (принцип относительности); 2) скорость распространения света одинакова по всем направлениям для всех инерциальных систем отсчета (принцип постоянства скорости света). Как показал А. Эйнштейн, на этих основных принципах его теории могут быть обоснованы способы измерения всех физических величин. Важнейшая физическая величина, характеризующая все изменения в природе, — время — измеряется при помощи световых сигналов, вследствие чего скорость света вошла во все формулы теории относительности. § 2. Преобразования Лоренца.
Допустим, что один из законов физики, полученный относительно системы отсчета S, имеет вид f (x, y, z, t...)= 0,
а относительно системы отсчета S ' имеет вид
. f' (x', y', z', t'...)= 0
Согласно принципу относительности, функции f и f ' должны иметь одинаковый вид. Это возможно, если между результатами измерения физических величин относительно S и S ' существуют определенные соотношения. А. Эйнштейн показал, что из двух принципов его теории следует, что координаты движущихся тел и время, измеренные относительно S и S ', связаны между собой преобразованиями Лоренца. Действительно, возьмем две координатные системы: нештрихованную XYZ (условно неподвижную) и штрихованную X 'Y ' Z' (условно подвижную, рис.), находящиеся в относительном движении. Оси обеих систем возьмем параллельными, постоянную относительную скорость υ системы X 'Y 'Z' относительно системы XYZ направим вдоль оси ОХ и предположим, что в исходный момент времени (t= 0; t' =0) начала координат обеих систем совпадают. При этих условиях легко показать, что координаты у и г преобразуются очевидным соотношением: у'=у; z’ = z, и мы ими заниматься не будем. Рассмотрим, как преобразуются координата x: и время t. Возьмем точку, соответствующую началу координат подвижной системы; ее координата х', очевидно, равна нулю: x’= 0 (1) Координата х этой же точки (в неподвижной системе) в момент времени t (отсчитанный в неподвижной системе) равна: x=υt Это равенство перепишем в виде: x - υt = 0 (2)
Сопоставляя равенства (1) и (2), замечаем, что в одной и той же точке пространства обращаются в нуль величины х’ (в штрихованной системе) и x - υt (в нештрихованной), поэтому естественно предположить, что х' и x - υt для любых моментов времени отличаются друг от друга лишь постоянным множителем а: x’ = а(x - υt) (3) Теперь рассмотрим точку, соответствующую началу координат неподвижной системы; ее координата х в этой системе равна нулю: x = 0 (4) В подвижной системе эта же точка в момент времени t’ (отсчитанный в подвижной системе) имеет координату x’, равную: x’= - υt откуда для этой точки имеет место равенство: x’ + υt’ = 0 Сопоставляя последнее равенство с равенством (4), характеризующим ту же точку в другой системе, положим, как и выше: х =a (x’ + υt’). (5) То, что коэффициенты пропорциональности а формул (3) и (5) должны быть одинаковыми, легко показать, основываясь на опытном положении об эквивалентности обеих систем, т. е. на невозможности установить, какая из систем находится в абсолютном движении. Для нахождения закона преобразования надо определить коэффициент а. Используем для этого опытный факт, согласно которому скорость светового сигнала, измеренная в обеих системах, даст одно и то же значение с. Пустим световой сигнал в момент совпадения обоих начал координат (этот момент в обеих системах будем считать начальным: t = t’ = 0) в направлении оси ОХ (О'Х'}. В произвольные моменты t(t’) сигналы в обеих системах будут доходить до точек, координаты которых определятся соответственно равенствами: x=ct; x’=ct’ (6) Перемножим уравнения (3) и (5) и подставим в полученный результат вместо х и х' их значения по (6); после сокращения найдем: c 2= a 2(c 2 – υ 2); для а возьмем положительное значение корня этого уравнения:
Найденное значение а позволяет написать преобразование координат в виде:
Отсюда легко найти и преобразование времени. Из второго равенства получаем:
Подставляя х' из первого соотношения, найдем:
Решая это равенство относительно t’, получим:
Аналогичным приемом получим для t:
Объединяя все полученные соотношения, напишем выражение координат и времени в подвижной системе через координаты и время в неподвижной:
y’=y; z’=z; (7)
и выражение координат и времени в неподвижной системе через координаты и время в подвижной:
y=y’; z=z’ (8)
Формулы (7) и (8) выражают преобразование координат и времени при переходе от одной системы отсчета к другой. Преобразования такого вида называются преобразованиями Лоренца. Преобразования Лоренца (7) и (8) переходят в преобразования Галилея при стремлении к нулю отношения β = υ/c. Заметим, что штрихованная и нештрихованная системы эквивалентны и преобразование (7) получается из преобразования (8) заменой знака относительной скорости. Преобразования Лоренца выведены из опытных положений. Теория относительности обобщает этот вывод и считает, что всякий физический закон должен удовлетворять преобразованием Лоренца. Это означает, что закон природы, выраженный математически в координатах одной системы, должен сохранять свой вид при переходе к координатам другой системы по формулам (7) или (8), т. е. должен быть инвариантен по отношению к преобразованию Лоренца. Уравнения механики Ньютона, будучи инвариантными по отношению к преобразованию Галилея, не инвариантны по отношению к преобразованию Лоренца. Развитие идей теории относительности привело к изменению уравнений Ньютона в том смысле, что были установлены уравнения механики, инвариантные по отношению к преобразованию Лоренца и переходящие в уравнения Ньютона в предельном случае бесконечно малого отношения β = υ/c. Проверка следствий новых уравнений механики на опыте показала правильность этих новых уравнений. Что же касается уравнений электродинамики (уравнений Максвелла), то они оказались инвариантными относительно преобразований Лоренца. Таким образом, выяснилось, что законы классической физики в области электромагнетизма удовлетворяют требованиям теории относительности, а в области механики (ньютоновской) справедливы лишь для скоростей υ «c и в общем случае требуют изменений. Обратим внимание на то, что для скоростей υ > с преобразования Лоренца теряют смысл. Это соответствует тому, что тела не могут двигаться со скоростями, превышающими скорость света.
§ 2. Следствия из преобразований теории относительности.
Рассмотрим наиболее важные следствия преобразований Лоренца.
а) Длина тел в разных системах. Преобразования Лоренца показывают, что одно и то же тело имеет разные линейные размеры в системе, в которой оно покоится, и в системе, находящейся в движении по отношению к этому телу. Предположим, что некоторый стержень, покоящийся в системе ХУZ, расположен в направлении оси ОХ и имеет в этой системе длину l (равную разности координат его конца и начала): l=x 2 – x 1 . Какова длина этого стержня в штрихованной координатной системе, движущейся относительно стержня со скоростью υ в направлении его длины? Для того чтобы найти эту длину l, нужно ее выразить как разность координат конца и начала стержня в штрихованной системе х 2 ’ и x 1 ’, при этом, пользуясь преобразованиями Лоренца, надо координаты х 2 ’ и x 1 ’ взять в один и тот же момент времени, определенный в штрихованной, системе. Таким образом, связывая х 2 ’ и x 1 ’ с x 2 и x 1надо брать формулу (8), содержащую время штрихованной системы; полагая это время постоянным, имеем:
откуда следует: x 2 ’ – x 1 ’= (x 2 – x 1) Стержень в координатной системе, движущейся относительно него, короче, чем в системе, где стержень покоится: Если бы мы взяли стержень, покоящийся в штрихованной системе, длина его была бы l’= x 2 ’ – x1’; в нештрихованной системе его длина будет l= x 2 – x 1; теперь надо измерения вести в один к тот же момент времени нештрихованной системы l. Пользуясь преобразованиями Лоренца (7), выражаем x 2 и x 1через x 2 ’ и x1’. Имеем: x2 – x1= (x2 ‘– x1 ‘) т. е. снова стержень длиннее в системе, в которой он покоится. Заметим, что размеры тел в направлении осей ОУ и ОZ одинаковы в обеих системах. Этот вывод теории относительности заменяет гипотезу о сокращении размеров тел, движущихся относительно эфира. По теории относительности стержень имеет наибольшую длину в той системе, относительно которой он покоится.
б) Длительность события в разных системах. Длительность события также различна в разных координатных системах. Предположим, что в точке А с координатой х в нештрихованной координатной системе ХУZ, происходит некоторое событие, длительность которого равна τ = t2 – t1, где t2 и t1 моменты времени конца и начала этого события, отсчитанные в координатной системе ХУZ. Какова будет длительность τ ‘= t2 ‘– t1’ этого события в штрихованной координатной системе Х'У’Z’. Моментам t1 и t2, отмеченным в координатной системе ХУZ, соответствуют моменты, t2’ и t1’ отмеченные в координатной системе Х'У'Z' для точки А, т. е. для одного и того же значения координаты х. Нам, следовательно, надо применить формулу преобразования (8), связывающую t’ и t при одном и том же значении х. Таким образом, имеем: t1’ откуда следует
Промежуток τ ' будет больше τ. Можно поставить и обратную задачу. Пусть в штрихованной системе (х’ постоянно) длительность некоего события τ ' = t’2 – t’1 . Какова будет длительность этого события в нештрихованной системе? Для ответа используем преобразование (8), в котором х' положим постоянным. Тогда получим: τ = τ’ / Теперь промежуток τ будет больше τ’. Отсюда получаем следующее заключение: длительность события, происходящего в некоторой точке А, меньше по отношению к той координатной системе^ относительно которой точка А покоится.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.019 с.) |

 Итак, гребец L, чтобы попасть в пункт В, должен направить свою лодку вверх по течению вдоль линии АР, причем если АР = 5 м (путь, который лодка проходит относительно воды за 1 сек), то его снесет на 4 м вниз по течению из Р в Q (расстояние, на которое сносит течение в 1 сек). При этом точка Q лежит на прямой АВ, а угол AQP прямой. По теореме Пифагора (AQ)2 + 42 = 52, откуда (AQ)2 = 25—16 = 9, а AQ = 3 м. Таким образом, лодка ежесекундно проходит вдоль А В расстояние 3 м, и, чтобы попасть из А в В, гребцу придется затратить 90/3=30 сек.
Итак, гребец L, чтобы попасть в пункт В, должен направить свою лодку вверх по течению вдоль линии АР, причем если АР = 5 м (путь, который лодка проходит относительно воды за 1 сек), то его снесет на 4 м вниз по течению из Р в Q (расстояние, на которое сносит течение в 1 сек). При этом точка Q лежит на прямой АВ, а угол AQP прямой. По теореме Пифагора (AQ)2 + 42 = 52, откуда (AQ)2 = 25—16 = 9, а AQ = 3 м. Таким образом, лодка ежесекундно проходит вдоль А В расстояние 3 м, и, чтобы попасть из А в В, гребцу придется затратить 90/3=30 сек. е к точке А. В один и тот же момент времени из А посылаются два световых сигнала вдоль отрезков АС и АВ. Эти сигналы попадают на зеркала и отражаются обратно к А. Распространение световых сигналов аналогично движению лодок в приведенном выше примере. Так как распространение света представляет собой волновой процесс в эфире, то каждый сигнал распространяется со скоростью 300000 км/сек относительно эфира, подобно тому как каждая из лодок движется со скоростью 5 м/сек относительно воды. Кроме того, эфир перемещается в направлении от А к С со скоростью и км/сек, аналогично воде, которая течет со скоростью 4 м/сек.
е к точке А. В один и тот же момент времени из А посылаются два световых сигнала вдоль отрезков АС и АВ. Эти сигналы попадают на зеркала и отражаются обратно к А. Распространение световых сигналов аналогично движению лодок в приведенном выше примере. Так как распространение света представляет собой волновой процесс в эфире, то каждый сигнал распространяется со скоростью 300000 км/сек относительно эфира, подобно тому как каждая из лодок движется со скоростью 5 м/сек относительно воды. Кроме того, эфир перемещается в направлении от А к С со скоростью и км/сек, аналогично воде, которая течет со скоростью 4 м/сек. . Из этой записи видно, какой будет величина коэффициента сжатия в других случаях, Иное объяснение было предложено и 1905 г. Эйнштейном.
. Из этой записи видно, какой будет величина коэффициента сжатия в других случаях, Иное объяснение было предложено и 1905 г. Эйнштейном.
 ;
; 



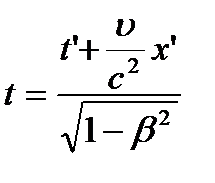
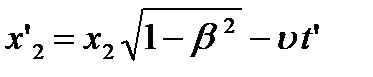 ;
; 
 или l’=l
или l’=l 


