
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы излучения абсолютно черного телаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Спектральная плотность излучения абсолютно черного тела является универсальной функцией длины волны и температуры. Это значит, что спектральный состав и энергия излучения абсолютно черного тела не зависят от природы тела. Формулы (1.1) и (1.2) показывают, что зная спектральную и интегральную плотность излучения абсолютно черного тела, можно вычислить их для любого нечерного тела, если известен коэффициент поглощения последнего, который должен быть определен экспериментально. Исследования привели к следующим законам излучения абсолютно черного тела. 1. Закон Стефана — Больцмана: Интегральная плотность излучения абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры
R=σT4
Величина σ называется постоянной Стефана — Больцмана: σ = 5,6687·10-8 Дж·м - 2·с - 1 ·К – 4. Энергия, испускаемая за время t абсолютно черным телом с излучающей поверхностью S при постоянной температуре Т,
W=σT4St
Если же температура тела изменяется со временем, т.е. Т = Т (t), то
Закон Стефана — Больцмана указывает на чрезвычайно быстрый рост мощности излучения с возрастанием температуры. Например при повышении температуры с 800 до 2400 К (т.е. с 527 до 2127° С) излучение абсолютно черного тела возрастает в 81 раз. Если абсолютно черное тело окружено средой с температурой Т0, то око будет поглощать энергию, излучаемую самой средой. В этом случае разность между мощностью испускаемого и поглощаемого излучений можно приближенно выразить формулой
U=σ(T4 – T04)
К реальным телам закон Стефана — Больцмана не применим, как наблюдения показывают более сложную зависимость R от температуры, а также — от формы тела и состояния его поверхности. 2. Закон смещения Вина. Длина волны λ0, на которую приходится максимум спектральной плотности излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре тела:
λ0=
Константа b, называемая постоянной закона Вина, равна b = 0,0028978 м · К (λ выражена в метрах). Таким образом, при повышении температуры растет не только полное излучение, но, кроме того, изменяется распределение энергии по спектру. Например, при малых температурах тела изучают главным образом инфракрасные лучи, а по мере повышения температуры излучение делается красноватым, оранжевым и, наконец, белым. На рис. 2.1 показаны эмпирические кривые распределения энергии излучения абсолютно черного тела по длинам волн при разных температурах: из них видно, что максимум спектральной плотности излучения при повышении температуры смещается в сторону коротких волн. 3. Закон Планка. Закон Стефана — Больцмана и закон смещения Вина не решают основной задачи о том, как велика спектральная плотность излучения, приходящаяся на каждую длину волны в спектре абсолютно черного тела при температуре Т. Для этого надо установить функциональную зависимость и от λ и Т. Основываясь на представлении о непрерывном характере испускания электромагнитных волн и на законе равномерного распределения энергии по степеням свободы (принятых в классической физике), были получены две формулы для спектральной плотности и лучения абсолютно черного тела: 1) формула Вина
где a и b — постоянные величины; 2) формула Рэлея — Джинса
uλТ = 8 πkT λ – 4 ,
Таким образом классическая физика оказалась неспособной объяснить закон распределения энергии в спектре излучения абсолютно черного тела. Для определения вида функции uλТ понадобились совершенно новые идеи о механизме испускания света. В 1900 г. М. Планк высказал гипотезу, что поглощение и испускание энергии электромагнитного излучения атомами и молекулами возможно только отдельными «порциями», которые получили название квантов энергии. Величина кванта энергии ε пропорциональна частоте излучения v (обратно пропорциональна длине волны λ):
ε = hv = hc/λ
Коэффициент пропорциональности h = 6,625·10-34 Дж·с и называется постоянной Планка. В видимой части спектра для длины волны λ = 0.5 мкм величина кванта энергии равна:
ε = hc/λ= 3.79·10-19 Дж·с = 2.4 эВ
На основании этого предположения Планком была получена формула для uλТ:
где k – постоянная Больцмана, с – скорость света в вакууме. л Кривая, соответствующая функции (2.1), так же показана на рис. 2.2. Из закона Планка (2.11) получаются закон Стефана - Больцмана и закон смещения Вина. Действительно, для интегральной плотности излучения получаем
Расчет по этой формуле дает результат, совпадающий с эмпирическим значением постоянной Стефана — Больцмана. Закон смещения Вина и его константу можно получить из формулы Планка нахождением максимума функции uλТ, для чего берется производная от uλТ по λ, и приравнивается нулю. Вычисление приводит к формуле:
Расчет постоянной b по этой формуле также дает результат, совпадающий с эмпирическим значением постоянной Вина. Рассмотрим важнейшие применения законов теплового излучения.
В § 1 было сказано, что глаз обладает чувствительностью только к очень узкому участку спектра (от 380 до 770 нм); все остальные волны не оказывают зрительного ощущения. Максимальная чувствительность глаза соответствует длине волны λ = 0,555 мкм. Исходя из этого свойства глаза следует требовать от источников света такого распределения энергии в спектре, при котором максимальная спектральная плотность излучения падала бы на длину волны λ = 0,555 мкм или около нее. Если в качестве такого источника взять абсолютно черное тело, то по закону смещения Вина можно вычислить его абсолютную температуру:
Таким образом, наиболее выгодный тепловой источник света должен иметь температуру в 5200 К, что соответствует температуре солнечной поверхности. Такое совпадение является результатом биологического приспособления человеческого зрения к распределению энергии в спектре солнечного излучения. Но и у этого источника света коэффициент полезного действия (отношение энергии видимого излучения к полной энергии всего излучения) будет невелик. Графически на рис. 2.3 этот коэффициент выражается отношением площадей S1 и S; площадь S1 выражает энергию излучения видимой области спектра, S — всю энергию излучения. Расчет показывает, что при температуре около 5000—6000 К световой к. п. д. равен всего 14—15% (для абсолютно черного тела). При температуре же существующих искусственных источников света ( Важнейшие из современных температурных источников света — это электрические лампы накаливания с вольфрамовой нитью. Температура плавления вольфрама равна 3655 К. Однако нагрев нити до температур выше 2500 К опасен, так как вольфрам при этой температуре очень быстро распыляется, и нить разрушается. Для уменьшения распыления нити было предложено наполнять лампы инертными газами (аргон, ксенон, азот) при давлении около 0,5 атм. Это позволило поднять температуру нити до 3000—3200 К. При этих температурах максимум спектральной плотности излучения лежит в области инфракрасных волн (около 1,1 мкм), поэтому все современные лампы накаливания имеют к. п. д. немногим больший 1%. Б. Оптическая пирометрия. Изложенные выше законы излучения черного тела позволяют определять температуру этого тела, если известна длина волны λ0, соответствующая максимуму uλТ (по закону Вина), или если известна величина интегральной плотности излучения (по закону Стефана — Больцмана). Эти методы определения температуры тела по его тепловому излучению на кают я оптической пирометрией; они особенно удобны при измерении очень высоких температур. Так как упомянутые законы применимы только к абсолютно черному телу, то оптическая пирометрия, основанная на них, дает хорошие результаты только при измерении температур тел, близких по своим свойствам к абсолютно черному. На практике таковыми являются заводские печи, лабораторные муфельные печи, топки котлов и т. п. Рассмотрим три способа определения температуры тепловых излучателей: а. Метод, основанный на законе смещения Вина. Если нам известна та длина волны, на которую приходится максимум спектральной плотности излучения, то температура тела может быть вычислена по формуле (2.2). В частности, таким способом определяется температура на поверхности Солнца, звезд и т. д. Для нечерных тел этот способ не дает истинную температуру тела; если в спектре излучения имеется один максимум и мы рассчитаем Т по формуле (2.2), то расчет дает нам температуру абсолютно черного тела, имеющего почти такое же распределение энергии в спектре, как и испытуемое тело. При этом цветность излучения абсолютно черного тела будет одинакова с цветностью исследуемого излучения. Такая температура тела называется его цветовой температурой. Цветовая температура нити лампы накаливания равна 2700—3000 К, что очень близко к ее истинной температуре. б. Радиационный способ измерения температур основан на измерении интегральной плотности излучения тела R и вычисления его температуры о закону Стефана — Больцмана. Соответствующие приборы называются радиационными пирометрами. Естественно, что если излучающее тело не является абсолютно черным, то радиационным пирометр не даст истинной температуры тела, а покажет ту температуру абсолютно черного тела, при которой интегральная плотность излучения последнего равна интегральной плотности излучения испытуемого тела. Такая температура тела называется радиационной, или энергетической, температурой. Из недостатков радиационного пирометра укажем на невозможность его применения для определения температур небольших объектов, а также на влияние среды, находящейся между объектом и пирометром, которая поглощает часть излучения. в. Я ркостный метод определения температур. Принцип действия его основан на визуальном сравнении яркости раскаленной нити лампы пирометра с яркостью изображения накаленного испытуемого тела. Прибор представляет собой зрительную трубу с помещенной внутри электрической лампой, питаемой от аккумулятора. Равенство зрительно наблюдаемое через монохроматический фильтр, определяется по исчезновению изображения нити на фоне изображения раскаленного тела. Накал нити регулируется реостатом, а температура определяется по шкале амперметра, градуированного прямо на температуру. Фотоэффект
Схема экспериментальной установки для исследования фотоэффекта изображена на рис. 1.
 очищена. К электродам прикладывалось некоторое напряжение U, полярность которого можно было изменять с помощью двойного ключа. Один из электродов (катод K) через кварцевое окошко освещался монохроматическим светом некоторой длины волны λ. При неизменном световом потоке снималась зависимость силы фототока I от приложенного напряжения. На рис. 2 изображены типичные кривые такой зависимости, полученные при двух значениях интенсивности светового потока, падающего на катод. очищена. К электродам прикладывалось некоторое напряжение U, полярность которого можно было изменять с помощью двойного ключа. Один из электродов (катод K) через кварцевое окошко освещался монохроматическим светом некоторой длины волны λ. При неизменном световом потоке снималась зависимость силы фототока I от приложенного напряжения. На рис. 2 изображены типичные кривые такой зависимости, полученные при двух значениях интенсивности светового потока, падающего на катод.
Кривые показывают, что при достаточно больших положительных напряжениях на аноде A фототок достигает насыщения, так как все электроны, вырванные светом из катода, достигают анода. Тщательные измерения показали, что ток насыщения I н прямо пропорционален интенсивности падающего света. Когда напряжение на аноде отрицательно, электрическое поле между катодом и анодом тормозит электроны. Анода могут достичь только те электроны, кинетическая энергия которых превышает | eU |. Если напряжение на аноде меньше, чем – U з, фототок прекращается. Измеряя U з, можно определить максимальную кинетическую энергию фотоэлектронов: (mυ 2 / 2) max = eU з
 К удивлению ученых, величина U з оказалась независящей от интенсивности падающего светового потока. Тщательные измерения показали, что запирающий потенциал линейно возрастает с увеличением частоты ν света (рис. 3). К удивлению ученых, величина U з оказалась независящей от интенсивности падающего светового потока. Тщательные измерения показали, что запирающий потенциал линейно возрастает с увеличением частоты ν света (рис. 3).Многочисленными экспериментаторами были установлены следующие основные закономерности фотоэффекта: 1. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты света ν и не зависит от его интенсивности. 2. Для каждого вещества существует так называемая красная граница фотоэффекта, т. е. наименьшая частота νmin, при которой еще возможен внешний фотоэффект. 3. Число фотоэлектронов, вырываемых светом из катода за 1 с, прямо пропорционально интенсивности света. 4. Фотоэффект практически безынерционен, фототок возникает мгновенно после начала освещения катода при условии, что частота света ν > νmin. Все эти закономерности фотоэффекта в корне противоречили представлениям классической физики о взаимодействии света с веществом. Согласно волновым представлениям при взаимодействии с электромагнитной световой волной электрон должен был бы постепенно накапливать энергию, и потребовалось бы значительное время, зависящее от интенсивности света, чтобы электрон накопил достаточно энергии для того, чтобы вылететь из катода. Как показывают расчеты, это время должно было бы исчисляться минутами или часами. Однако, опыт показывает, что фотоэлектроны появляются немедленно после начала освещения катода. В этой модели также было невозможно понять существование красной границы фотоэффекта. Волновая теория света не могла объяснить независимость энергии фотоэлектронов от интенсивности светового потока и пропорциональность максимальной кинетической энергии частоте света. Таким образом, электромагнитная теория света оказалась неспособной объяснить эти закономерности. Выход был найден А. Эйнштейном в 1905 г. Теоретическое объяснение наблюдаемых закономерностей фотоэффекта было дано Эйнштейном на основе гипотезы М. Планка о том, что свет излучается и поглощается определенными порциями, причем энергия каждой такой порции определяется формулой E = h ν, где h – постоянная Планка. Эйнштейн сделал следующий шаг в развитии квантовых представлений. Он пришел к выводу, что свет имеет прерывистую (дискретную) структуру. Электромагнитная волна состоит из отдельных порций – квантов, впоследствии названных фотонами. При взаимодействии с веществом фотон целиком передает всю свою энергию h ν одному электрону. Часть этой энергии электрон может рассеять при столкновениях с атомами вещества. Кроме того, часть энергии электрона затрачивается на преодоление потенциального барьера на границе металл–вакуум. Для этого электрон должен совершить работу выхода Aвых, зависящую от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь вылетевший из катода фотоэлектрон, определяется законом сохранения энергии:
Эту формулу принято называть уравнением Эйнштейна для фотоэффекта. С помощью уравнения Эйнштейна можно объяснить все закономерности внешнего фотоэффекта. Из уравнения Эйнштейна следуют линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света, существование красной границы, безынерционность фотоэффекта. Общее число фотоэлектронов, покидающих за 1 с поверхность катода, должно быть пропорционально числу фотонов, падающих за то же время на поверхность. Из этого следует, что ток насыщения должен быть прямо пропорционален интенсивности светового потока. Это утверждение носит название закона Столетова. Как следует из уравнения Эйнштейна, тангенс угла наклона прямой, выражающей зависимость запирающего потенциала U з от частоты ν (рис. 3), равен отношению постоянной Планка h к заряду электрона e: Это позволяет экспериментально определить значение постоянной Планка. Такие измерения были выполнены в 1914 г. Р. Милликеном и дали хорошее согласие со значением, найденным Планком. Эти измерения позволили также определить работу выхода A:
где c – скорость света, λкр – длина волны, соответствующая красной границе фотоэффекта. У большинства металлов работа выхода A составляет несколько электрон-вольт (1 эВ = 1,602·10-19 Дж). В квантовой физике электрон-вольт часто используется в качестве энергетической единицы измерения. Значение постоянной Планка, выраженное в электрон–вольтах в секунду, равно h =4.136·10-15 эВ·с. Среди металлов наименьшей работой выхода обладают щелочные элементы. Например, у натрия A = 1,9 эВ, что соответствует красной границе фотоэффекта λкр ≈ 680 нм. Поэтому соединения щелочных металлов используют для создания катодов в фотоэлементах, предназначенных для регистрации видимого света. Итак, законы фотоэффекта свидетельствуют, что свет при испускании и поглощении ведет себя подобно потоку частиц, получивших название фотонов или световых квантов. Таким образом, учение о свете, совершив виток длительностью в два столетия, вновь возвратилось к представлениям о световых частицах – корпускулах. Но это не был механический возврат к корпускулярной теории Ньютона. В начале XX века стало ясно, что свет обладает двойственной природой. При распространении света проявляются его волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом – корпускулярные (фотоэффект). Эта двойственная природа света получила название корпускулярно-волнового дуализма. Позже двойственная природа была открыта у электронов и других элементарных частиц. Классическая физика не может дать наглядной модели сочетания волновых и корпускулярных свойств у микрообъектов. Движением микрообъектов управляют не законы классической механики Ньютона, а законы квантовой механики. Теория излучения абсолютно черного тела, развитая М. Планком, и квантовая теория фотоэлектрического эффекта Эйнштейна лежат в основании этой современной науки. Кроме рассмотренного нами внешнего фотоэффекта (называемого обычно просто фотоэффектом), существует также внутренний фотоэффект, наблюдаемый в диэлектриках и полупроводниках. Он заключается в обусловленном действием света перераспределении электронов по энергетическим уровням. В этом случае электроны выделяются во всем объеме.
В области р-n перехода или на грани металла с полупроводником может наблюдаться вентильный фотоэффект. Он заключается в возникновении под действием света электродвижущей силы (фото-э.д.с). На рис. 173 показан ход потенциальной энергии электронов (сплошная кривая) и дырок (пунктирная кривая) в области р-n перехода. Неосновные для данной области носители (электроны в р -области и дырки в n -области), возникшие под действием света, проходят через переход. В результате в p -области накапливается избыточный положительный заряд, в n -области — избыточный отрицательный заряд. Это приводит к возникновению приложенного к переходу напряжения, которое и представляет собой фотоэлектродвижущую силу. В частности этот эффект используется при создании солнечных батарей.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 7240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.83.202 (0.016 с.) |


 или λ0Т = b.
или λ0Т = b.

 где k — постоянная Больцмана. Опытная проверка показала, что для данной температуры формула Вина верна для коротких волн (когда λТ очень мало и дает резкие схождения опытом в области длинных волн. Формула Рэлея — Джинса оказалась верна для длинных волн и совершенно не применима для коротких (рис. 2.2).
где k — постоянная Больцмана. Опытная проверка показала, что для данной температуры формула Вина верна для коротких волн (когда λТ очень мало и дает резкие схождения опытом в области длинных волн. Формула Рэлея — Джинса оказалась верна для длинных волн и совершенно не применима для коротких (рис. 2.2). (2.1)
(2.1)
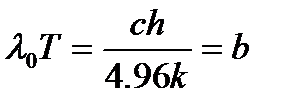 (2.2)
(2.2) А. Тепловые источники света. Большинство искусственных источников света является тепловыми излучателями (электрические лампы накаливания, обычные дуговые лампы и т. д.). Однако эти источники света не являются достаточно экономичными.
А. Тепловые источники света. Большинство искусственных источников света является тепловыми излучателями (электрические лампы накаливания, обычные дуговые лампы и т. д.). Однако эти источники света не являются достаточно экономичными. К
К 3000 К) этот к. п. д. составляет всего около 1—3%. Такая невысокая «световая отдача» теплового излучателя объясняется тем, что при хаотическом движении атомов и молекул возбуждаются не только световые (видимые), по и другие электромагнитные волны, которые не оказывают светового воздействия н глаз. Поэтому невозможно избирательно заставить тело излучать только те волны, к которым чувствителен глаз: обязательно излучаются и невидимые волны.
3000 К) этот к. п. д. составляет всего около 1—3%. Такая невысокая «световая отдача» теплового излучателя объясняется тем, что при хаотическом движении атомов и молекул возбуждаются не только световые (видимые), по и другие электромагнитные волны, которые не оказывают светового воздействия н глаз. Поэтому невозможно избирательно заставить тело излучать только те волны, к которым чувствителен глаз: обязательно излучаются и невидимые волны. Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г. Герцем и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света.
Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г. Герцем и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света.

 На внутреннем фотоэффекте основано действие так называемых фотосопротивлений. Количество образующихся носителей тока пропорционально падающему световому потоку. Поэтому фотосопротивления применяются для целей фотометрии. Первым полупроводником, нашедшим применение для этих целей, был селен.
На внутреннем фотоэффекте основано действие так называемых фотосопротивлений. Количество образующихся носителей тока пропорционально падающему световому потоку. Поэтому фотосопротивления применяются для целей фотометрии. Первым полупроводником, нашедшим применение для этих целей, был селен. 


