
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики и законы теплового излучения.Содержание книги
Поиск на нашем сайте
ЛЕКЦИЯ 9 ХАРАКТЕРИСТИКИ И ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ. Излучение и поглощение энергии. Характеристики теплового излучения. Закон Кирхгофа. Законы Стефана — Больцмана и смещения Вина Излучение и поглощение энергии. Если на какое-либо тело падает поток излучения Фо, то часть потока Фотр<Фо отражается от поверхности тела обратно: от матовой поверхности – диффузно во все стороны, от гладкой поверхности – зеркально. При не слишком большой толщине слоя часть падающего излучения пройдет насквозь и за телом будет наблюдаться поток излучения Фпрох<Фо. Наконец, часть потока, проникающего в тело, будет поглощаться и превращаться в другие формы энергии, в конечном счете – в тепло (рис.9.1).

Фпогл
Рис.9.1. Распределение потока излучения, падающего на полупрозрачную пластину. Используя закон сохранения энергии, можно записать: Фо = Фотр + Фпогл + Фпрох. (9.1) Разделив обе части равенства (9.1) на Фо, получим:
Отношение (коэффициент поглощения).
Итак, можно записать 1 = r + а + D. (9.3) Величина D, характеризующая прозрачность тела, зависит от толщины последнего. При достаточной толщине любое тело практически непрозрачно. Необходимо отметить возможность очень сильной зависимости D от длины волны. Например, чистый кремний непрозрачен для видимого света при толщинах более 1000 Å (заметим, что при меньшей толщине все вещества прозрачны в видимой части спектра), однако в инфракрасной области он остается прозрачным. На дне океана из «прозрачной» морской воды – всегда тьма… Большинство же твердых тел непрозрачно уже при сравнительно небольшой толщине. В этом случае D = 0 и 1 = r + а. Отражательная способность r такого тела зависит от атомного строения тела, состояния его поверхности (зеркальная или матовая), спектральной характеристики падающего на него излучения. Тело, которое абсолютно не поглощает падающее излучение и полностью отражает все падающие на него лучи, называется абсолютно белым телом. Для него а = 0; r = 1. Наблюдаемый цвет такого тела полностью определяется спектральным составом освещающего его излучения. Тело, полностью поглощающее все падающее на него излучение, называется абсолютно черным телом. Для него а = 1; r = 0. При освещении такого тела любым источником света оно не будет ничего отражать и представляется черным. Например, для сажи в области видимого света а» 0.99, что и обусловливает ее черный цвет. Однако в инфракрасной области коэффициент отражения сажи увеличивается и абсолютно черной ее уже считать нельзя. Тело, поглощательная способность которого меньше единицы, но одинакова для всех длин волн, называется серым телом. Сюда относится большинство реальных тел. Исследования показывают, отражательная и поглощательная способности веществ зависят не только от длины волн облучения, но и от температуры. Поэтому обычно анализируют соответствующие зависимости аl,Т и r l,Т, между которыми по-прежнему существует взаимосвязь: r l,Т = 1 - аl,Т. (9.4) Зависимость аl,Т и r l,Т от длины волны обусловливают видимую окраску несамосветящегося тела. Тело, интенсивно поглощающее излучение всех длин волн, кроме, например, зеленого (l» 550 нм), при освещении его белым светом будет выглядеть зеленым. При освещении такого тела монохроматическим «незеленым» светом, такое тело ничего не отражает и выглядит черным. Так что каждое несамосветящееся тело обладает не цветом, а лучеотражательной способностью. Если нет облучения, то нет и цвета. «Ночью все кошки серы». «Холодное свечение», как следствие физического явления флуоресценции предоставляется интересующемуся студенту для самостоятельного изучения. Закон Кирхгофа Кирхгоф, опираясь на второй закон термодинамики и анализируя условия равновесного излучения в изолированной системе тел, установил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности есть величина постоянная, оно не зависит от природы тела и является для всех тел универсальной функцией частоты (длины волны) и температуры (закон Кирхгофа):
Таким образом, универсальная функция Кирхгофа rl,T есть не что иное, как спектральная плотность энергетической светимости абсолютно черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре. Из закона Кирхгофа следует, что спектральная плотность энергетической светимости любого реального тела в любой области спектра всегда меньше спектральной плотности энергетической светимости черного тела (при тех же значениях Т и v), так как аl,Т < 1 и поэтому Rl,T<rl,T. Кроме того, из (9.7) вытекает, что если тело при данной температуре T не поглощает электромагнитные волны в интервале частот от v до v +d v, то оно их в этом интервале частот при температуре T и не излучает, так как при аl,Т =0 Rl,Т = 0. Используя закон Кирхгофа, выражение для энергетической светимости тела (17.3) можно записать в виде
Для серого тела
где
- энергетическая светимость абсолютно черного тела, зависящая только от температуры. СЛЕДСТВИЯ ЗАКОНА КИРХГОФА: ЛЕКЦИЯ 10 Формулы Рэлея — Джинса Из рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа rl,T не дал желаемых результатов, так как все константы получены эмпирическим путем, и механизм излучения энергии нагретым телом оставался неясным. Следующая строгая попытка теоретического вывода зависимости rl,T принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877 - 1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы. Формула Рэлея-Джинса для спектральной плотности энергетической светимости черного тела имеет вид
где С использованием зависимости
Как показал опыт, выражение (17.13) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея - Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 10.1).
Рис. 10.1. Теория Рэлея – Джинса и реальное излучение абсолютно черного тела.
Этот результат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.
Формула Планка Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями – квантами, причем энергия кванта пропорциональна частоте колебания:
где h = 6,625×10-34 Дж×с — постоянная Планка. Планк вывел для универсальной функции Кирхгофа формулы
которые блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот (длин волн) и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседании Немецкого физического общества. Этот день стал датой рождения квантовой физики. Сам Макс Планк в объективное существование квантов не поверил до конца своих дней в 1947 году. Ход его рассуждений: «Я построил теорию, позволяющую получить хорошее совпадение с экспериментом». Однако значение теории Планка в физике трудно переоценить. · Во-первых, она позволяет получить не только совпадение со всеми эмпирическими законами по форме, но и дает возможность с поразительной точностью вычислить константы законов. · Во-вторых, термодинамические теории Рэлея-Джинса и Вина получаются из теории Планка как частные предельные случаи. · В-третьих, введение в физику квантов произвело переворот в познании микромира и в настоящее время само существование физики без квантов невозможно. В качестве подтверждения всесильности планковской теории излучения получим из формулы Планка закон Стефана-Больцмана. По определению энергетической светимости абсолютно черного тела
где, по теории Планка
Учитывая константы, не зависящие от длины волны излучения
Чтобы вычислить этот не самый простой интеграл, сделаем подстановку
Тогда
Таким образом, получается
по форме совпадающее с законом Стефана-Больцмана Re = s T4, но самое удивительное заключается в том, что подстановка в (10.5) значений констант после вычислений дает именно 5,67×10-8 Вт/(м2×К4). В области малых частот, т. е. при h Закон смещения Вина получим с помощью формул (10.4) после дифференцирования по l и приравнивания производной нулю. Второй закон Вина может быть получен после дифференцирования формул (10.4) по Т. Более того, вычисленные константы С1 и С2 близки к экспериментальным. Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка. ЛЕКЦИЯ 9 ХАРАКТЕРИСТИКИ И ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ. Излучение и поглощение энергии. Характеристики теплового излучения. Закон Кирхгофа. Законы Стефана — Больцмана и смещения Вина
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.42.189 (0.009 с.) |






 Фо
Фо

 Фотр
Фотр




 Фпрох
Фпрох (9.2)
(9.2) Безразмерное отношение
Безразмерное отношение  называется лучеотражательной или просто отражательной способностью или коэффициентом отражения.
называется лучеотражательной или просто отражательной способностью или коэффициентом отражения.
 называется лучепоглощательной способностью тела
называется лучепоглощательной способностью тела Наконец, отношение
Наконец, отношение 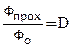 можно назвать лучепропускательной способностью или коэффициентом пропускания излучения.
можно назвать лучепропускательной способностью или коэффициентом пропускания излучения. (9.7)
(9.7)
 (9.8)
(9.8)
 (10.1)
(10.1) - средняя энергия осциллятора с собственной частотой v. Для классического осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы, поэтому средняя энергия каждой колебательной степени свободы
- средняя энергия осциллятора с собственной частотой v. Для классического осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы, поэтому средняя энергия каждой колебательной степени свободы  зависимость (10.1) может быть представлена в виде:
зависимость (10.1) может быть представлена в виде: (10.2)
(10.2)
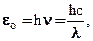 (10.3)
(10.3)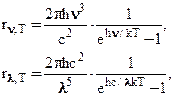 (10.4)
(10.4)


 Интеграл
Интеграл 
 , (10.5)
, (10.5) (энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка совпадает с формулой Рэлея — Джинса. Для доказательства этого достаточно разложить экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами.
(энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка совпадает с формулой Рэлея — Джинса. Для доказательства этого достаточно разложить экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами.


