
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Всякое тело наиболее энергично излучает то, что оно наиболее интенсивно поглощает.Содержание книги
Поиск на нашем сайте
Абсолютно черное тело является наиболее эффективным излучателем при всех длинах волн и всех температурах. Закон Кирхгофа описывает только тепловое излучение, являясь настолько характерным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое закону Кирхгофа не подчиняется, не является тепловым. Законы Стефана — Больцмана и смещения Вина (эмпирические законы излучения абсолютно черного тела) Из закона Кирхгофа следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения. Австрийский физик И. Стефан (1835—1893), анализируя экспериментальные данные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости Re от температуры. Согласно закону Стефана – Больцмана,
т. е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; s — постоянная Стефана — Больцмана: ее экспериментальное значение равно 5,67×10-8 Вт/(м2×К4). Закон Стефана-Больцмана, определяя зависимость Re от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции rl,T от длины волны l при различных температурах (рис. 9.4) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости rl,T от l и осью абсцисс, пропорциональна энергетической светимости Re черного тела и, следовательно, по закону Стефана-Больцмана, четвертой степени температуры.
Рис. 9.4. Зависимость спектральной плотности энергетической светимости абсолютно черного тела от температуры.
Немецкий физик В. Вин (1864—1928), опираясь на законы термо- и электродинамики, установил зависимость длины волны l max, соответствующей максимуму функции rl,T от температуры T. Согласно закону смещения Вина,
т. е. длина волны l max соответствующая максимальному значению спектральной плотности энергетической светимости rl,T черного тела, обратно пропорциональна его термодинамической температуре, С1 - постоянная Вина; ее экспериментальное значение равно 2,9×10-3 м×К. Выражение (9.10) потому называют законом смещения Вина, что оно показывает смещение положения максимума функции rl,T по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).
Другим эмпирическим законом излучения абсолютно черным телом, установленным В. Вином, был закон, позволявший определять максимальное значение функции, представленной на графиках рис.9.4. Этот закон утверждает, что максимум спектральной плотности энергетической светимости абсолютно черного тела пропорционален пятой степени абсолютной температуры:
где ЛЕКЦИЯ 10 ХАРАКТЕРИСТИКИ И ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ. Формулы Рэлея — Джинса и Планка. Тепловое излучение реальных (серых) тел. Формулы Рэлея — Джинса Из рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа rl,T не дал желаемых результатов, так как все константы получены эмпирическим путем, и механизм излучения энергии нагретым телом оставался неясным. Следующая строгая попытка теоретического вывода зависимости rl,T принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877 - 1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы. Формула Рэлея-Джинса для спектральной плотности энергетической светимости черного тела имеет вид
где С использованием зависимости
Как показал опыт, выражение (17.13) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея - Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 10.1).
Рис. 10.1. Теория Рэлея – Джинса и реальное излучение абсолютно черного тела.
Этот результат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.
Формула Планка Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями – квантами, причем энергия кванта пропорциональна частоте колебания:
где h = 6,625×10-34 Дж×с — постоянная Планка. Планк вывел для универсальной функции Кирхгофа формулы
которые блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот (длин волн) и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседании Немецкого физического общества. Этот день стал датой рождения квантовой физики. Сам Макс Планк в объективное существование квантов не поверил до конца своих дней в 1947 году. Ход его рассуждений: «Я построил теорию, позволяющую получить хорошее совпадение с экспериментом». Однако значение теории Планка в физике трудно переоценить. · Во-первых, она позволяет получить не только совпадение со всеми эмпирическими законами по форме, но и дает возможность с поразительной точностью вычислить константы законов. · Во-вторых, термодинамические теории Рэлея-Джинса и Вина получаются из теории Планка как частные предельные случаи. · В-третьих, введение в физику квантов произвело переворот в познании микромира и в настоящее время само существование физики без квантов невозможно. В качестве подтверждения всесильности планковской теории излучения получим из формулы Планка закон Стефана-Больцмана. По определению энергетической светимости абсолютно черного тела
где, по теории Планка
Учитывая константы, не зависящие от длины волны излучения
Чтобы вычислить этот не самый простой интеграл, сделаем подстановку
Тогда
Таким образом, получается
по форме совпадающее с законом Стефана-Больцмана Re = s T4, но самое удивительное заключается в том, что подстановка в (10.5) значений констант после вычислений дает именно 5,67×10-8 Вт/(м2×К4). В области малых частот, т. е. при h Закон смещения Вина получим с помощью формул (10.4) после дифференцирования по l и приравнивания производной нулю. Второй закон Вина может быть получен после дифференцирования формул (10.4) по Т.
Более того, вычисленные константы С1 и С2 близки к экспериментальным. Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.29 (0.011 с.) |

 (9.9)
(9.9)
 (9.10)
(9.10) (911)
(911)
 (10.1)
(10.1) - средняя энергия осциллятора с собственной частотой v. Для классического осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы, поэтому средняя энергия каждой колебательной степени свободы
- средняя энергия осциллятора с собственной частотой v. Для классического осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы, поэтому средняя энергия каждой колебательной степени свободы  зависимость (10.1) может быть представлена в виде:
зависимость (10.1) может быть представлена в виде: (10.2)
(10.2)
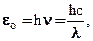 (10.3)
(10.3)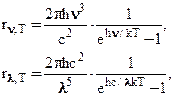 (10.4)
(10.4) ,
,


 Интеграл
Интеграл 
 , (10.5)
, (10.5) (энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка совпадает с формулой Рэлея — Джинса. Для доказательства этого достаточно разложить экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами.
(энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка совпадает с формулой Рэлея — Джинса. Для доказательства этого достаточно разложить экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами.


