
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Кирхгофа. Абсолютно черное телоСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Среднее значение плотности потока энергии (т. е. потока энергии через единичную площадку, нормаль к которой совпадает с направлением переноса энергии), переносимой волной, принято называть интенсивностью. Плотность потока энергии, испускаемой излучающим телом во всех направлениях, называют энергетической светимостью тела Тепловое излучение представляет собой совокупность волн с различными частотами w или длинами волн l. Введем обозначение
где
Вместо частоты w излучение можно характеризовать длиной волны l. Участку спектра d w в этом случае будет соответствовать диапазон длин волн d l. Дифференцируя выражение
где с – скорость света в вакууме. Знак «минус» во втором выражении не имеет существенного значения, он лишь указывает на то, что с возрастанием одной величины другая убывает. Поэтому знак «минус» в дальнейшем писать не будем. Тогда
Если диапазоны d w и d l, входящие в выражения (2.1) и (2.3), соответствуют одному и тому же интервалу dR, т. е.
Соотношение (2.4) устанавливает взаимосвязь между плотностями потока энергии приходящимися на единичные интервалы частоты и длины волны. Пусть на элементарную площадку поверхности тела падает поток лучистой энергии
называется поглощательной способностью тела. Поглощательная способность тела зависит от частоты и температуры. По определению, значение Испускательная (
Сами значения величин
Можно создать устройство, достаточно близкое по своим свойствам к абсолютно черному телу. Схематическое изображение АЧТ представлено на рис. 2.1. Оно представляет собой почти замкнутую полость с малым отверстием. Излучение, проникшее внутрь через отверстие, прежде чем выйти обратно из отверстия, претерпевает многократные отражения от зачерненной поверхности. При каждом отражении часть энергии поглощается, в результате чего практически все излучение поглощается такой полостью.
3. Закон Стефана – Больцмана и закон Вина. Теоретическое объяснение законов излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к появлению квантовой теории. Долгое время попытки получить теоретический вид функции
где s = 5,7 × 10-8 Вт / (м2×К4) есть постоянная Стефана – Больцмана; Т – абсолютная температура. Формула (3.1) является математической формулировкой закона Стефана – Больцмана. Таким образом, вывод, к которому пришел Стефан для серых тел, оказался справедливым только для абсолютно черных тел. Воспользовавшись, кроме термодинамики, электромагнитной теорией, в 1893 г. В. Вин показал, что функция спектрального распределения энергии излучения должна иметь вид
где F – некоторая функция отношения частоты к температуре. Для функции
где
Попытка объяснить вид кривых теплового излучения (рис. 3.1), исходя из законов классической физики, была сделана Рэлеем и Джинсом. Из уравнений Максвелла для электромагнитного поля следует, что, с энергетической точки зрения, «черное» излучение в полости эквивалентно излучению системы из бесконечно большого числа не взаимодействующих друг с другом гармонических излучателей (радиационных осцилляторов), собственные частоты которых равны частотам соответствующих компонентов «черного» излучения. Методами статистической физики Рэлей и Джинс получили следующее выражение
Отметим особенность формулы Рэлея – Джинса: заряд осциллятора, масса осциллятора, все частные свойства осциллятора не входят в полученное выражение. На рис. 3.2 показана зависимость испускательной способности f (w) АЧТ от частоты. Кривая с максимумом – это экспериментальная зависимость (подобная кривым на рис. 3.1); другая кривая построена по формуле Рэлея – Джинса (3.5). В области малых частот (больших длин волн) значения функции (3.5) довольно хорошо согласуются с экспериментом. Представленные на рис. 3.2 зависимости расходятся в области высоких частот (коротких длин волн). Такое расхождение расчетных и экспериментальных данных получило название «ультрафиолетовая катастрофа». И только отказ от некоторых представлений классической физики позволил дать объяснение свойствам излучения черного тела.
Формула Планка В 1900 г. немецкому физику Максу Планку удалось найти вид функции
где n – частота излучения; h – коэффициент пропорциональности, получивший название постоянной Планка, h = 6.625 × 10-34 Дж × с;
Плотность распределения радиационных осцилляторов была подсчитана Планком классически. Согласно распределению Больцмана, число частиц Nn, энергия каждой из которых равна e n, определяется формулой
где А – нормировочный множитель; k – постоянная Больцмана. Используя определение среднего значения дискретных величин, получаем выражение для средней энергии частиц, которое равно отношению полной энергии частиц к полному числу частиц:
где
Последующие преобразования приводят к соотношению
Таким образом, функция Кирхгофа, с учетом (3.4), имеет вид
Формула (4.3) называется формулой Планка. Эта формула согласуется с экспериментальными данными во всем интервале частот от 0 до
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.170.2 (0.014 с.) |

 . Единица измерения
. Единица измерения  для потока энергии, испускаемый единицей поверхности тела в интервале частот d w. При малом интервале d w поток
для потока энергии, испускаемый единицей поверхности тела в интервале частот d w. При малом интервале d w поток  , (2.1)
, (2.1) - спектральная испускательная способность, т. е. плотность потока энергии, испускаемой телом в единичном интервале частот. Испускательная способность зависит от температуры тела. Энергетическая светимость, или интегральная испускательная способность, связана со спектральной испускательной способностью соотношением
- спектральная испускательная способность, т. е. плотность потока энергии, испускаемой телом в единичном интервале частот. Испускательная способность зависит от температуры тела. Энергетическая светимость, или интегральная испускательная способность, связана со спектральной испускательной способностью соотношением .
. , получаем
, получаем , (2.2)
, (2.2) . (2.3)
. (2.3) , то с учетом (2.2) получаем
, то с учетом (2.2) получаем . (2.4)
. (2.4) , обусловленный электромагнитными волнами, частота которых заключена в интервале d w. Часть этого потока (
, обусловленный электромагнитными волнами, частота которых заключена в интервале d w. Часть этого потока ( ) будет поглощена телом. Безразмерная величина, определяемая соотношением
) будет поглощена телом. Безразмерная величина, определяемая соотношением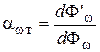 ,
,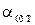 не может быть больше 1. Для тела, полностью поглощающего падающее на него излучение во всем диапазоне частот,
не может быть больше 1. Для тела, полностью поглощающего падающее на него излучение во всем диапазоне частот,  . Такое тело называется абсолютно черным телом (АЧТ). Тело, для которого
. Такое тело называется абсолютно черным телом (АЧТ). Тело, для которого  , называется серым.
, называется серым.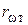 ) и поглощательная (
) и поглощательная ( ,
,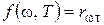 . Таким образом, универсальная функция Кирхгофа
. Таким образом, универсальная функция Кирхгофа  есть не что иное, как испускательная способность абсолютно черного тела. Если пользоваться функцией Кирхгофа для длины волны
есть не что иное, как испускательная способность абсолютно черного тела. Если пользоваться функцией Кирхгофа для длины волны 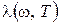 , то связь между функциями следующая:
, то связь между функциями следующая: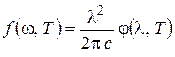 . (2.5)
. (2.5) Абсолютно черных тел в природе не существует, однако если в ограниченном диапазоне частот (или длин волн) поглощательная способность тела зависит от w и T так же, как и у АЧТ, то такое тело можно считать абсолютно черным в определенном интервале частот. Например, сажа или платиновая чернь имеют поглощательную способность
Абсолютно черных тел в природе не существует, однако если в ограниченном диапазоне частот (или длин волн) поглощательная способность тела зависит от w и T так же, как и у АЧТ, то такое тело можно считать абсолютно черным в определенном интервале частот. Например, сажа или платиновая чернь имеют поглощательную способность  , (3.1)
, (3.1)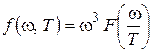 ,
, с учетом (2.5) получается выражение
с учетом (2.5) получается выражение , (3.2)
, (3.2) – некоторая функция произведения
– некоторая функция произведения  . Соотношение (3.2) позволяет установить зависимость между длиной волны
. Соотношение (3.2) позволяет установить зависимость между длиной волны  , на которую приходится максимум функции
, на которую приходится максимум функции 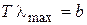 , (3.3)
, (3.3) где b = 2.9 × 10-3 м × К – универсальная постоянная. Формула (3.3) получила название закона Вина, или закона смещения Вина. Экспериментальные зависимости испускательной способности абсолютно черного тела от длины волны показаны на рис. 3.1. Разные кривые соответствуют различным значениям температуры АЧТ. Площадь под каждой кривой численно равна энергетической светимости АЧТ при соответствующей температуре. Из анализа представленных на рис. 3.1 результатов следует, что энергетическая светимость АЧТ возрастает с увеличением температуры. Максимум испускательной способности, а следовательно, и
где b = 2.9 × 10-3 м × К – универсальная постоянная. Формула (3.3) получила название закона Вина, или закона смещения Вина. Экспериментальные зависимости испускательной способности абсолютно черного тела от длины волны показаны на рис. 3.1. Разные кривые соответствуют различным значениям температуры АЧТ. Площадь под каждой кривой численно равна энергетической светимости АЧТ при соответствующей температуре. Из анализа представленных на рис. 3.1 результатов следует, что энергетическая светимость АЧТ возрастает с увеличением температуры. Максимум испускательной способности, а следовательно, и  с увеличением температуры сдвигается в сторону более коротких волн.
с увеличением температуры сдвигается в сторону более коротких волн. , (3.4)
, (3.4) где
где  – величина, пропорциональная плотности радиационных осцилляторов; e – средняя энергия осциллятора. По классическому закону о равномерном распределении энергии по степеням свободы системы, находящейся в термодинамическом равновесии e = kT, формула Рэлея – Джинса принимает вид
– величина, пропорциональная плотности радиационных осцилляторов; e – средняя энергия осциллятора. По классическому закону о равномерном распределении энергии по степеням свободы системы, находящейся в термодинамическом равновесии e = kT, формула Рэлея – Джинса принимает вид . (3.5)
. (3.5) ,
,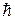 = h /2p =
= h /2p = , то его энергия e n должна быть кратной этой величине:
, то его энергия e n должна быть кратной этой величине: (4.1)
(4.1)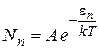 , n = 1, 2, 3… (4.2)
, n = 1, 2, 3… (4.2)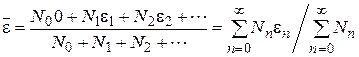 ,
,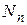 число частиц, обладающих энергией
число частиц, обладающих энергией  . С учетом (4.1) и (4.2) выражение для среднего значения энергии частиц имеет вид
. С учетом (4.1) и (4.2) выражение для среднего значения энергии частиц имеет вид .
.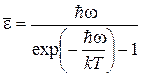 .
. . (4.3)
. (4.3)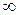 . В области малых частот, согласно правилам приближенных вычислений, при (
. В области малых частот, согласно правилам приближенных вычислений, при ( ):
):  »
»  и
и  выражение (4.3) преобразуется в формулу Рэлея – Джинса.
выражение (4.3) преобразуется в формулу Рэлея – Джинса.


