
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Излучение Вавилова – ЧеренковаСодержание книги Поиск на нашем сайте
В 1934 г. советские ученые С. И. Вавилов и П. А. Черенков обнаружили свечение, возникающее у разнообразных веществ под действием b-лучей (потока электронов). Излучением Вавилова – Черенкова называется отличное от люминесценции излучение света, которое возникает при движении заряженных частиц в веществе со скоростями v, большими фазовой скорости В процессе излучения энергия и скорость излучающей свободной частицы уменьшаются вследствие торможения частицы. Однако, в отличие от тормозного излучения заряженной частицы, являющегося следствием изменения скорости, уменьшение скорости частицы в эффекте Вавилова – Черенкова само является следствием излучения. Иными словами, если бы убыль энергии частицы на излучение Вавилова – Черенкова удавалось каким-либо образом восполнять и частица двигалась в веществе с постоянной скоростью v, то излучение Вавилова – Черенкова все равно наблюдалось бы, а тормозного излучения в этом случае не было. Дадим объяснение этому эффекту с точки зрения классической физики. Заряженная частица вызывает кратковременную поляризацию вещества в окрестностях тех точек, через которые она проходит при своем движении. Поэтому молекулы среды, лежащие на пути частицы, становятся кратковременно действующими когерентными источниками электромагнитных колебаний, интерферирующих при наложении. Пусть заряженная частица движется со скоростью v (
Для каждого значения l длиныволныизлучения можно найти такое значение
Рис. 7.1 При Если частица движется в веществе со скоростью
Для направления a = j разность хода элементарных волн, излучаемых из любых двух точек А и В траектории заряженной частицы, равна нулю:
Следовательно, элементарные волны, распространяющиеся в направлении a = j, взаимно усиливаются при интерференции, образуя результирующее излучение в этом направлении. Свет, возникающий на каждом малом участке траектории заряженной частицы, распространяется вдоль образующей конуса, вершина которого О расположена на этом участке, ось совпадает с траекторией частицы, а образующая составляет с осью угол j. Свет поляризован так, что вектор Е направлен по нормали к поверхности конуса, а вектор Н по касательной к ней. Рассмотрим теперь то же самое явление с корпускулярной точки зрения. Пусть до излучения электрон (движущаяся частица) обладал энергией
Умножим второе равенство скалярно на скорость электрона и воспользуемся известным приближенным соотношением
(здесь скорость электрона не изменяется при акте излучения). Тогда из (7.3) и (7.4) получаем:
что совпадает с результатом (7.2). Эффект Комптона Импульс фотона слишком мал и не поддается прямому измерению. Однако при столкновении фотона со свободным электроном величину передаваемого импульса уже можно измерить. Процесс рассеяния фотона на свободном электроне называется эффектом Комптона. Выведем соотношение, связывающее длину волны рассеянного фотона с углом рассеяния и длиной волны фотона до соударения. Пусть фотон с импульсом р и энергией Е = pc сталкивается с неподвижным электроном, энергия которого
Рис. 8.1 Импульс электрона отдачи будет равен Согласно закону сохранения энергии
Запишем закон сохранения импульса:
Возведем (8.2) в квадрат:
Учитывая, что релятивистская энергия
Переходя к длинам волн p =
или окончательно:
Величина В своем опыте Комптон использовал рентгеновское излучение с известной длиной волны и обнаружил, что у рассеянных фотонов длина волны увеличивается. На рис. 8.1 приведены результаты экспериментального исследования рассеяния монохроматического рентгеновского излучения на графите. Первая кривая (Q = 0°) характеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния Q, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс длина волны. На всех графиках присутствует несмещенный компонент излучения (левый пик). Его наличие объясняется рассеянием первичного излучения на связанных электронах атома. Эффект Комптона и внешний фотоэффект подтвердили гипотезу о квантовой природе света, т. е. свет действительно ведет себя так, как если бы он состоял из частиц, энергия которых h n и импульс h /l. Вместе с тем, явления интерференции и дифракции света могут быть объяснены с позиции волновой природы. Оба эти подхода в настоящий момент представляются взаимодополняющими друг друга.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.01 с.) |

 света в этом веществе. Условие существования этого излучения с / n < v < с, где n – коэффициент преломления вещества.
света в этом веществе. Условие существования этого излучения с / n < v < с, где n – коэффициент преломления вещества. ) вдоль оси х и в моменты времени t и t + D t находится, соответственно, в точках А и В, расстояние между которыми l = v D t (рис. 7.1). Разность хода Dэлементарных волн, которые излучаются из точек А и В и распространяются с фазовой скоростью
) вдоль оси х и в моменты времени t и t + D t находится, соответственно, в точках А и В, расстояние между которыми l = v D t (рис. 7.1). Разность хода Dэлементарных волн, которые излучаются из точек А и В и распространяются с фазовой скоростью  в направлении n, составляющем угол a с вектором v, есть
в направлении n, составляющем угол a с вектором v, есть .
. , при котором D = l/2, так что элементарные волны гасят друг друга:
, при котором D = l/2, так что элементарные волны гасят друг друга: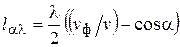 .
.
 . Расстояние от М до N равно
. Расстояние от М до N равно  . Поэтому при равномерном прямолинейном движении заряженной частицы в веществе со скоростью
. Поэтому при равномерном прямолинейном движении заряженной частицы в веществе со скоростью  частица не излучает.
частица не излучает. , то значение
, то значение  . (7.2)
. (7.2) .
.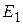 и импульсом
и импульсом  , после излучения –
, после излучения –  и
и  . После излучения импульс фотона равен -
. После излучения импульс фотона равен - 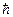 k, где модуль волнового вектора определяется отношением частоты к фазовой скорости света в веществе:
k, где модуль волнового вектора определяется отношением частоты к фазовой скорости света в веществе:  . Тогда законы сохранения энергии и импульса имеют вид
. Тогда законы сохранения энергии и импульса имеют вид . (7.3)
. (7.3) (7.4)
(7.4) ;
;  ;
;  ;
;  ,
, . После соударения импульс фотона равен
. После соударения импульс фотона равен  и направлен под углом Q, как показано на рис. 8.1.
и направлен под углом Q, как показано на рис. 8.1.
 , и полная релятивистская энергия
, и полная релятивистская энергия 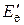 . Здесь мы используем релятивистскую механику, поскольку скорость электрона может достигать значений, близких к скорости света.
. Здесь мы используем релятивистскую механику, поскольку скорость электрона может достигать значений, близких к скорости света. или
или  , преобразуется к виду
, преобразуется к виду . (8.1)
. (8.1) .(8.2)
.(8.2) и вычтем это выражение из (8.1):
и вычтем это выражение из (8.1):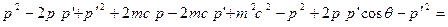
 . (8.3)
. (8.3)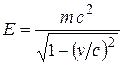 , можно показать, что правая часть выражения (8.2) равна
, можно показать, что правая часть выражения (8.2) равна  . Тогда после преобразования импульс фотона равен
. Тогда после преобразования импульс фотона равен .
. = h /l, Dl = l - l¢, получаем:
= h /l, Dl = l - l¢, получаем: ,
, . (8.4)
. (8.4) называется комптоновской длиной волны. Для электрона комптоновская длина волны l c = 0.00243 нм.
называется комптоновской длиной волны. Для электрона комптоновская длина волны l c = 0.00243 нм.


