
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения импульса. Соударение двух телСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
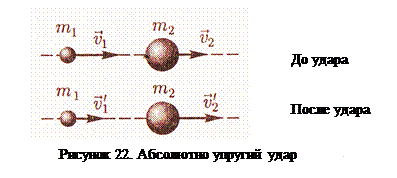
Основной закон динамики поступательного движения для замкнутой системы тел: Таким образом, импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Этот закон справедлив не только в классической механике, но и в квантовой механике для замкнутых систем микрочастиц. Закон сохранения импульса - фундаментальный закон природы. Закон справедлив и для незамкнутых систем, если геометрическая сумма всех внешних сил равна нулю. Из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным. В неинерциальных системах отсчета закон сохранения импульса несправедлив. При соударении двух тел существуют 2 предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические виды энергии. При таком ударе кинетическая энергия полностью или частично переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, модуль и направления которых определяются двумя условиями: сохранением полной механической энергии и сохранением полного импульса системы тел. При абсолютно упругом центральном ударе (удар происходит по прямой, соединяющей центры масс шаров) возможны два случая:
Положим, что система замкнутая и вращение шаров отсутствует. Пусть массы шаров m1 и m2, скорости их до удара
Если m1= m2, то Для численных расчетов нужно спроектировать векторы скоростей на ось, вдоль которой движутся шары, т.е. учесть направление скоростей соответствующими знаками. Из полученных формул можно определить скорость шара после удара о движущуюся или неподвижную стенку:
Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации при таком ударе не возникает. Кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. После удара столкнувшиеся тела либо двигаются с одинаковой скоростью, либо покоятся (рисунок 23).
.
При абсолютно неупругом ударе выполняется лишь закон сохранения импульса системы. Закон сохранения механической энергии не выполняется. Рассмотрим абсолютно неупругий удар 2-х материальных точек, образующих замкнутую систему. Пусть массы материальных точек m1 и m2, а скорости до удара - Скорость системы тел после удара В численных расчетах используются проекции векторов скоростей на направление оси, вдоль которой двигаются тела. Контрольные вопросы: 1. Изложите закон сохранения импульса. 2. Расскажите об абсолютно упругом ударе. 3. Какие законы сохранения действуют при абсолютно упругом ударе? 4. Как определить скорости двух тел после абсолютно упругого удара? 5. Что такое абсолютно неупругий удар? Какой закон сохранения действует при абсолютно неупругом ударе? 6. Как вычислить скорость тел после абсолютно неупругого удара? Выберите правильные ответы на поставленные вопросы:
Закон всемирного тяготения Изучением движения планет люди занимались, начиная с глубокой древности. Астроном Иоганн Кеплер обработал результаты многочисленных наблюдений и изложил законы движения планет:
Впоследствии Ньютон на основании законов Кеплера и основных законов динамики открыл закон всемирного тяготения: Все тела (материальные точки) независимо от их свойств, притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними F = G G - гравитационная постоянная. G = 6,672 • 10-11 Сила тяжести Согласно второму закону Ньютона любое тело вблизи поверхности Земли начинает двигаться с ускорением свободного падения Для тел, находящихся на поверхности Земли: Если тело массой m находится на высоте h над поверхностью Земли, то
Работа в поле тяготения
Эта работа не зависит от траектории, а определяется лишь начальным и конечным положением тела. Следовательно, силы тяготения - консервативные, а поле тяготения – потенциальное.
Работа, совершаемая консервативными силами:
При R2®¥ Потенциальная энергия двух тел, находящихся на расстоянии Если тело массой m находится на высоте h над поверхностью Земли, то его потенциальная энергия R3- радиус Земли R3 = 6,4-106м, М - масса Земли. М = 6 × 1024 кг.
Невесомость Вес тела – это сила, действующая на опору или на подвес. Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости. Если к телу приложена не только сила тяготения Тогда вес тела Если тело покоится или движется равномерно и прямолинейно, то Если тело свободно движется в поле тяготения по любой траектории, то Космические скорости Первая космическая скорость Поэтому Вторая космическая скорость
Третья космическая скорость
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 6819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.108.8 (0.007 с.) |

 , следовательно:
, следовательно: 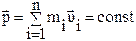 .
.
 и
и 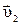 , а после удара
, а после удара 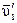 и
и 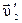 соответственно. Скорости шаров после удара определяются при решении системы уравнений, составленной согласно закону сохранения механической энергии и закону сохранения импульса:
соответственно. Скорости шаров после удара определяются при решении системы уравнений, составленной согласно закону сохранения механической энергии и закону сохранения импульса: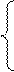
 - закон сохранения энергии.
- закон сохранения энергии.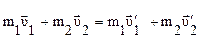 - закон сохранения импульса.
- закон сохранения импульса.
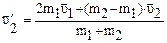
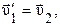
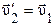 .
.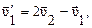
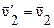 .
.

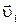 и
и 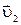 , а после удара -
, а после удара - 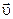 . Суммарный импульс системы после удара должен быть таким же, как и до удара
. Суммарный импульс системы после удара должен быть таким же, как и до удара 
 .
.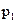 и
и  и кинетическими энергиями Е1 и Е2 соответственно, суммарный импульс Р шаров и кинетическая энергия Е сразу после соударения…
○ 1. …Р = р1+р2, E > E1+E2.
○ 2. …Р = р1+р2, E < E1+E2.
○ 3. …Р ≠ р1+р2, E = E1+E2.
○ 4. …Р = р1+р2, E = E1+E2.
○ 5. …Р ≠ р1+р2, E < E1+E2.
и кинетическими энергиями Е1 и Е2 соответственно, суммарный импульс Р шаров и кинетическая энергия Е сразу после соударения…
○ 1. …Р = р1+р2, E > E1+E2.
○ 2. …Р = р1+р2, E < E1+E2.
○ 3. …Р ≠ р1+р2, E = E1+E2.
○ 4. …Р = р1+р2, E = E1+E2.
○ 5. …Р ≠ р1+р2, E < E1+E2.
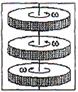 Уменьшится в три раза.
○ 5. Уменьшится в девять раз.
Уменьшится в три раза.
○ 5. Уменьшится в девять раз.
 Уменьшится согласно закону сохранения момента импульса.
○ 4. Увеличится, так как возрастет кинетическая энергия.
○ 5. Не изменится согласно закону сохранения энергии.
Уменьшится согласно закону сохранения момента импульса.
○ 4. Увеличится, так как возрастет кинетическая энергия.
○ 5. Не изменится согласно закону сохранения энергии.
 и
и 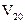 сталкиваются абсолютно неупруго и приобретают скорости
сталкиваются абсолютно неупруго и приобретают скорости 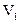 и
и 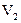 . Какое из утверждений справедливо?
○ 1. V1=V2=V, причем
. Какое из утверждений справедливо?
○ 1. V1=V2=V, причем 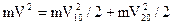 .
○ 2. V1=V2=V, причем
.
○ 2. V1=V2=V, причем  .
○ 3. V1≠V2, причем
.
○ 3. V1≠V2, причем  ○ 4. V1≠V2, причем
○ 4. V1≠V2, причем 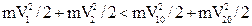 ○ 5. V1=V2=V, причем
○ 5. V1=V2=V, причем 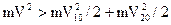 .
.
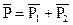 E=E1+E2
○ 2.
E=E1+E2
○ 2. 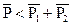 E<E1+E2
○ 3.
E<E1+E2
○ 3. 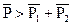 E>E1+E2
○ 4.
E>E1+E2
○ 4. 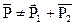 E≠E1+E2
○ 5.
E≠E1+E2
○ 5.  - постоянная величина, где R - радиус орбиты планеты (половина большой оси эллипса);
- постоянная величина, где R - радиус орбиты планеты (половина большой оси эллипса);  , где:
, где: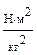
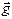 под действием силы тяжести
под действием силы тяжести  .
. 
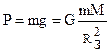 , где М - масса Земли, m - масса тела, R3 - радиус Земли. Отсюда:
, где М - масса Земли, m - масса тела, R3 - радиус Земли. Отсюда: 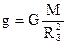
 . Таким образом, сила тяжести уменьшается с удалением от Земли.
. Таким образом, сила тяжести уменьшается с удалением от Земли.
 Если тело массой
Если тело массой 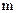 перемещать с расстояния от Земли
перемещать с расстояния от Земли  до расстояния
до расстояния 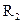 (рисунок 24), то работа по его перемещению:
(рисунок 24), то работа по его перемещению: 
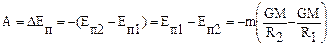
 ®0.
®0.
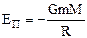 .
.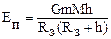 , где
, где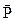 , но и другая сила
, но и другая сила 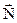 , создающая ускорение тела
, создающая ускорение тела 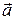 , то дополнительная сила
, то дополнительная сила 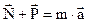 .
. =
=  .
.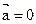 и
и 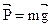 .
.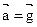 и
и 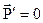 - тело будет невесомым.
- тело будет невесомым.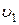 - это минимальная скорость тела, при которой оно становится спутником Земли и начинает двигаться вокруг Земли по круговой орбите радиусом
- это минимальная скорость тела, при которой оно становится спутником Земли и начинает двигаться вокруг Земли по круговой орбите радиусом 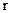 . Тогда сила тяготения Земли создает нормальное ускорение, равное
. Тогда сила тяготения Земли создает нормальное ускорение, равное 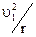 . По второму закону Ньютона
. По второму закону Ньютона 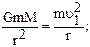
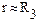 ;
; 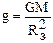 и
и  .
.
 - скорость, при которой тело преодолевает притяжение Земли и превращается в спутник Солнца. Для этого необходимо, чтобы кинетическая энергия тела была равна работе, совершаемой против сил тяготения.
- скорость, при которой тело преодолевает притяжение Земли и превращается в спутник Солнца. Для этого необходимо, чтобы кинетическая энергия тела была равна работе, совершаемой против сил тяготения.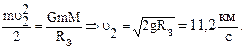
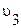 - позволяет телу покинуть Солнечную систему, преодолев притяжение Солнца.
- позволяет телу покинуть Солнечную систему, преодолев притяжение Солнца.  = 16,7
= 16,7 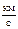 при условии запуска тела в направлении орбитального движения Земли. При запуске тела в противоположном направлении
при условии запуска тела в направлении орбитального движения Земли. При запуске тела в противоположном направлении 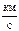 .
.


