
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физика и техника. Физика - наука о природеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление Введение.. 4 Физика и техника. Физика - наука о природе. 4 Интернациональная система единиц измерений СИ.…………………5 Правило вывода единиц измерения физических величин……………5 Механика. 7 Кинематика. 7 Система отсчета. Кинематические параметры материальной точки. 7 Движение материальной точки (МТ) по прямой и по окружности. 11 Движение материальной точки при действии гравитации. 14 Кинематика вращательного движения абсолютно твердого тела. 20 Динамика. 24 Инерциальные системы отсчета. Законы Ньютона. 24 Неинерциальные системы отсчета. Сила инерции. Центробежная сила. Сила Кориолиса 26 Механическая работа и мощность. 34 Кинетическая энергия материальной точки………………….............35 Потенциальная энергия. Полная механическая энергия……...36 Динамика вращения АТТ.. …39 Статика. 45 Законы сохранения в механике. 46 Закон сохранения энергии. Закон сохранения момента импульса. 46 Закон сохранения импульса. Соударение двух тел. 48 Закон всемирного тяготения. 52 Гидростатика. 56 Элементы релятивистской механики. 57 Преобразования Галилея. 57 Постулаты специальной теории относительности (Эйнштейна)…………………………………………………………..58 Преобразования Лоренца. 59 Следствия из преобразований Лоренца. 61 Интервал между событиями. 64 Основной закон релятивисткой динамики МТ.. 65 Закон взаимосвязи массы и энергии. 66
А н н о т а ц и я Настоящий конспект лекций разработан на факультете среднего профессионального образования Санкт-Петербургского университета информационных технологий, механики и оптики, рассмотрен предметно-цикловой комиссией естественнонаучных дисциплин и рекомендован для использования в учебном процессе факультета. Конспект лекций по механике предназначен для студентов учреждений среднего профессионального образования, закончивших не менее 9 классов общеобразовательной школы. В конспекте рассмотрены следующие темы: классические кинематика и динамика, законы сохранения, действующие в классической динамике, и элементы релятивистской механики. Полнота изложения тем соответствует требованиям программы теоретического минимума по физике СПб ГУ ИТМО. Введение Физика и техника. Физика - наука о природе Слово физика произошло от греческого слова "фюзис" (природа). Люди всю свою жизнь изучают природу и ее закономерности. Из физики выделились разные науки: химия, астрономия, электротехника, электроника и другие. Большое значение имело и имеет учение о материи и энергии. Весь мир вокруг нас, это материя и ее движение. Всеобщей мерой движения является энергия. Современная физика изучает различные формы движения материи, их взаимные превращения, а также свойства вещества и поля. Одним из основных механизмов изучения являются экспериментальные исследования, которые сопровождаются измерением тех или иных величин. При этом величиной называется все, что может быть выражено количественно, а измерением -сравнение значений исследуемой величины с эталоном. Значение величины, с которым сравнивают результаты ее измерения, называется единицей измерения. Величины, характеризующие физические свойства материи, называются физическими (длина, время, скорость и т.д.). Совокупность единиц измерения разных величин называется системой измерений. Правило вывода единиц измерения физических величин 1. Выбрать формулу, содержащую буквенное обозначение физической величины. 2. Алгебраически вывести из формулы значение этой величины. 3. В полученное выражение подставить все известные единицы измерения с их размерностями. 4. Выполнить все возможные алгебраические действия над размерностями, упрощающие выражения. 5. Принять полученный результат за искомую единицу измерения и дать ей название. Пример: Необходимо вывести единицу мощности. 1) Выбираем формулу для вычисления работы. Работа 2) Находим мощность: 3) Подставляем единицы измерения 4) Выполняем алгебраические действия 5) Назовем ее ватт (Вт). Размерность мощности - Механика Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. Основные законы классической механики установлены итальянским физиком Г.Галилеем и окончательно сформулированы английским ученым И.Ньютоном. Механика Галилея-Ньютона изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Для адекватного описания движения тел со скоростями, близкими к скорости света, создана релятивистская механика, в основе которой лежат труды А.Эйнштейна и Г.Лоренца.
Кинематика Кинематические параметры МТ
 (Рисунок 4). (Рисунок 4).
Средняя скорость движения за время Dt определяется соотношением
Направление средней скорости совпадает с направлением
Мгновенная скорость — это предел, к которому стремится средняя скорость за бесконечно малый промежуток времени.
 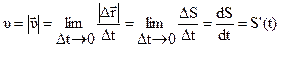
Ускорение Скорость тела может меняться как по модулю, так и по направлению. Изменение скорости характеризуется ускорением. Среднее ускорение:
Вектор мгновенного ускорения
Контрольные вопросы: 1. Что такое механика и чем она занимается? 2. Что такое кинематика? 3. Расскажите о системе отсчета МТ и о траектории. 4. Какие способы описания движения тел вы знаете? 5. Как вычисляется средняя скорость? 6. Как определить модуль и направление мгновенной скорости? 7. Что такое среднее ускорение и мгновенное ускорение? 8. На какие составляющие можно разложить ускорение при криволинейном движении? Абсолютно твердого тела Абсолютно твердым телом (АТТ) называется тело, которое ни при каких условиях не может деформироваться и при любых условиях расстояние между любыми двумя его точками остается постоянным. При вращении АТТ вокруг неподвижной оси (Рисунок 10) отдельные точки этого тела будут описывать окружности разных радиусов Быстрота вращения характеризуется углом Мгновенное значение угловой скорости Угловая скорость является векторной величиной

Поскольку направление угловой скорости выбрано произвольно, а сам вектор Средняя величина углового ускорения рассчитывается по формуле: Мгновенным угловым ускорением называется векторная величина, равная первой производной от угловой скорости по времени: Угловое ускорение тоже является псевдовектором. Если направление оси вращения не изменяется в пространстве, то векторы Модуль тангенциальной составляющей линейного ускорения вращающейся МТ, принадлежащей АТТ:

Модуль нормальной составляющей ускорения МТ:
где Длина пути, пройденного МТ по дуге окружности:
При равнопеременном вращении АТТ:
Плоское движение АТТ Плоским называется движение, при котором все точки тела движутся в параллельных плоскостях. Примером плоского движения является качение колеса без проскальзывания (Рисунок 11). Динамика Динамика – раздел механики, в котором рассматривается влияние взаимодействия между телами на их движение. Инерциальные системы отсчета. Существуют системы отсчета, относительно которых все тела, не взаимодействующие с другими телами, находятся в покое или движутся равномерно и прямолинейно. Такие системы называются инерциальными. В инерциальных системах отсчета (ИСО) явления природы описываются наиболее простыми уравнениями. Галилей доказал, что если существуют хотя бы одна ИСО, то существует и бесконечное множество таких систем. Всякая система отсчета, движущаяся относительно ИСО равномерно и прямолинейно тоже является инерциальной. Согласно преобразованиям Галилея скорость одного и того же тела в разных ИСО различна, но его ускорение относительно всех ИСО будет одинаковым. Телом, свободным от взаимодействия с другими телами, можно считать тело достаточно удаленное от других тел (например, уединенную звезду). Ускорение этого тела должно быть как можно ближе к нулю. Тогда систему отсчета, связанную с этим телом, можно считать инерциальной. В системе отсчета, связанной с поверхностью Земли, звезда, находящаяся на расстоянии r = 1016м от Земли, имеет ускорение: В системе отсчета, связанной с центром Земли (геоцентрическая) та же звезда имеет ускорение: В системе отсчета, связанной с центром Солнца (гелиоцентрическая) та же звезда имеет ускорение: При решении огромного числа практических задач по определению параметров движения тел по поверхности Земли и около нее инерциальной системой отсчета можно приближенно считать поверхность Земли, т.к.
Силой Единицей силы в системе СИ является 1 ньютон (Н). Масса есть мера инертности тела. Масса - это скалярная величина. Единицей массы в системе СИ является 1 килограмм (кг). Произведение массы тела на его скорость Ньютон назвал количеством движения тела. Теперь эта величина называется импульсом тела
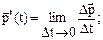 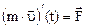 ; ; 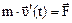 . Т.к. . Т.к. 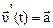 : :
Третий закон Ньютона
Динамика вращения АТТ При изучении вращения АТТ часто пользуются понятием момента инерции. Момент инерции тела – мера инерции твердых тел при вращательном движении. Термин момент всегда связан с вращением, при этом обязательно нужно указывать относительно чего вращается тело. Момент инерции материальной точки массой Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс "n" материальных точек системы на квадраты их расстояний до рассматриваемой оси.
В случае непрерывного распределения масс эта сумма сводится к интегралу Моменты инерции относительно оси вращения наиболее часто встречающихся тел сведены в таблицу. Таблица моментов инерции некоторых тел относительно оси вращения
Если известен момент инерции тела массой
Моментом силы
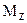 , равная проекции на эту ось вектора момента силы , равная проекции на эту ось вектора момента силы  , определенного относительно произвольной точки О данной оси z. Значение , определенного относительно произвольной точки О данной оси z. Значение  не зависит от выбора положения точки О на оси z. не зависит от выбора положения точки О на оси z.
Моментом импульса тела
 относительно точки О: относительно точки О:  , где , где  - плечо. - плечо.
 Моментом импульса относительно оси z называется скалярная величина Моментом импульса относительно оси z называется скалярная величина  , равная проекции на эту ось вектора момента импульса , равная проекции на эту ось вектора момента импульса 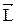 , определенного относительно произвольной точки О данной оси. , определенного относительно произвольной точки О данной оси.
Момент импульса АТТ относительно оси z:

Основной закон динамики вращательного движения АТТ:
Кинетическая энергия вращения тела находится как сумма кинетических энергий его элементарных объемов:
 . Поскольку угловая скорость всех элементарных объемов одна и та же . Поскольку угловая скорость всех элементарных объемов одна и та же  , то: Евр= , то: Евр=  . Таким образом: . Таким образом:
Работа, совершаемая при вращении АТТ, идет на увеличение его кинетической энергии:
В случае плоского движения АТТ его кинетическая энергия складывается из энергии поступательного движения и энергия вращательного движения Ic - момент инерции относительно оси, проходящей через центр масс. Центром масс системы называется точка С, положение которой задает радиус-вектор
Декартовы координаты центра масс:
В заключении сопоставим в виде таблицы основные величины и уравнения поступательного и вращательного движения тела. В приведенной таблице прослеживается аналогия конфигурации формул для расчета физических величин поступательного и вращательного движений.
Контрольные вопросы: 1. Что такое момент инерции тела? 2. Изложите теорему Штейнера. 3. Расскажите, что Вы знаете о моменте силы? 4. Что Вы знаете о моменте импульса АТТ? 5. Изложите закон динамики вращательного движения АТТ. 6. Как вычислить кинетическую энергию вращения АТТ? 7. Как вычислить кинетическую энергию плоского движения АТТ?
Выберите правильные ответы на поставленные вопросы
Статика Статикой называется раздел механики, в котором изучаются условия равновесия АТТ. Состоянием равновесия называется такое состояние тела, когда оно покоится, движется прямолинейно и равномерно или равномерно вращается вокруг неподвижной оси, проходящей через центр масс тела. Знание условий равновесия АТТ важно для расчетов машин и механизмов, транспортных средств и различных сооружений. Первое условие равновесия является следствием 2-го закона Ньютона Первое условие равновесия АТТ необходимое, но недостаточное, т.к. АТТ может не только двигаться поступательно, но и вращаться. Второе условие равновесия АТТ получается из основного уравнения динамики вращательного движения АТТ: Закон всемирного тяготения Изучением движения планет люди занимались, начиная с глубокой древности. Астроном Иоганн Кеплер обработал результаты многочисленных наблюдений и изложил законы движения планет:
Впоследствии Ньютон на основании законов Кеплера и основных законов динамики открыл закон всемирного тяготения: Все тела (материальные точки) независимо от их свойств, притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними F = G G - гравитационная постоянная. G = 6,672 • 10-11 Сила тяжести Согласно второму закону Ньютона любое тело вблизи поверхности Земли начинает двигаться с ускорением свободного падения Для тел, находящихся на поверхности Земли: Если тело массой m находится на высоте h над поверхностью Земли, то
Работа в поле тяготения
Эта работа не зависит от траектории, а определяется лишь начальным и конечным положением тела. Следовательно, силы тяготения - консервативные, а поле тяготения – потенциальное.
Работа, совершаемая консервативными силами:
При R2®¥ Потенциальная энергия двух тел, находящихся на расстоянии Если тело массой m находится на высоте h над поверхностью Земли, то его потенциальная энергия R3- радиус Земли R3 = 6,4-106м, М - масса Земли. М = 6 × 1024 кг.
Невесомость Вес тела – это сила, действующая на опору или на подвес. Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости. Если к телу приложена не только сила тяготения Тогда вес тела Если тело покоится или движется равномерно и прямолинейно, то Если тело свободно движется в поле тяготения по любой траектории, то Космические скорости Первая космическая скорость Поэтому Вторая космическая скорость
Третья космическая скорость | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


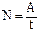





 =
=  .
.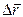 .
.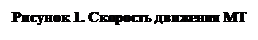
 — называется производной от перемещения по времени или дифференциалом функции перемещения.
— называется производной от перемещения по времени или дифференциалом функции перемещения. 

 Мгновенное ускорение:
Мгновенное ускорение:  ;
; при криволинейном движении обычно представляют в виде векторной суммы двух ускорений (Рисунок 3).
при криволинейном движении обычно представляют в виде векторной суммы двух ускорений (Рисунок 3). - тангенциальное ускорение, направленное по касательной к траектории (как и скорость
- тангенциальное ускорение, направленное по касательной к траектории (как и скорость 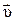 ), определяет быстроту изменения скорости по модулю;
), определяет быстроту изменения скорости по модулю;
 - нормальное ускорение (центростремительное), направленное по нормали (перпендикулярно) к касательной, определяет быстроту изменения скорости по направлению.
- нормальное ускорение (центростремительное), направленное по нормали (перпендикулярно) к касательной, определяет быстроту изменения скорости по направлению. и
и  перпендикулярны друг другу, поэтому модуль полного ускорения
перпендикулярны друг другу, поэтому модуль полного ускорения 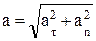
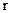 , центры которых лежат на оси вращения.
, центры которых лежат на оси вращения.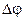 , на который поворачивается тело за единицу времени. При равномерном вращении
, на который поворачивается тело за единицу времени. При равномерном вращении  .
. .
.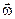 , характеризующей не только быстроту, но и направление вращения. Направлен вектор
, характеризующей не только быстроту, но и направление вращения. Направлен вектор 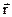

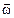 не имеет определенной точки приложения, то вектор
не имеет определенной точки приложения, то вектор  .
. .
. и
и  учитывая, что
учитывая, что  :
:
 ,
, - частота вращения
- частота вращения

 ;
;  , где:
, где: и
и  – начальные условия.
– начальные условия.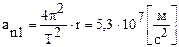 , где Т – период вращения Земли вокруг собственной оси. Поэтому данная система отсчета не может считаться инерциальной.
, где Т – период вращения Земли вокруг собственной оси. Поэтому данная система отсчета не может считаться инерциальной.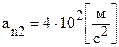 . Эта система тоже не может считаться инерциальной.
. Эта система тоже не может считаться инерциальной.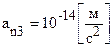 . Это ускорение близко к нулю и измерить его с помощью механических опытов пока не под силу самым точным современным приборам. Поэтому гелиоцентрическую систему отсчета можно считать инерциальной.
. Это ускорение близко к нулю и измерить его с помощью механических опытов пока не под силу самым точным современным приборам. Поэтому гелиоцентрическую систему отсчета можно считать инерциальной. , что значительно меньше ускорения свободного падения
, что значительно меньше ускорения свободного падения  . В этой формуле
. В этой формуле 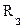 - радиус Земли,
- радиус Земли,  - период вращения Земли вокруг своей оси.
- период вращения Земли вокруг своей оси. Первый закон Ньютона:
Первый закон Ньютона: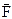 называется векторная величина, характеризующая воздействие на данное тело со стороны других тел или полей.
называется векторная величина, характеризующая воздействие на данное тело со стороны других тел или полей. . Формула справедлива для тел, движущихся поступательно (скорость всех точек тела одинакова).
. Формула справедлива для тел, движущихся поступательно (скорость всех точек тела одинакова). Второй закон Ньютона (основной закон динамики поступательного движения)
Второй закон Ньютона (основной закон динамики поступательного движения)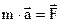
 Следовательно, все силы возникают попарно. Они приложены к разным телам и поэтому не могут уравновесить друг друга. Третий закон справедлив лишь в инерциальных системах отсчета. Он позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек.
Следовательно, все силы возникают попарно. Они приложены к разным телам и поэтому не могут уравновесить друг друга. Третий закон справедлив лишь в инерциальных системах отсчета. Он позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. относительно оси вращения:
относительно оси вращения:  , где
, где  - кратчайшее расстояние от МТ до оси.
- кратчайшее расстояние от МТ до оси.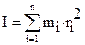
 .
.





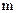 относительно оси, проходящей через его центр масс
относительно оси, проходящей через его центр масс 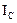 , то момент инерции этого тела
, то момент инерции этого тела  относительно любой другой параллельной оси определяется теоремой Штейнера:
относительно любой другой параллельной оси определяется теоремой Штейнера: , где
, где  - расстояние между осями.
- расстояние между осями. , проведенного из точки О в точку приложения силы на вектор силы.
, проведенного из точки О в точку приложения силы на вектор силы.  . Вектор
. Вектор 

 Модуль момента силы
Модуль момента силы 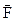 относительно точки О:
относительно точки О:  , где
, где  - плечо - кратчайшее расстояние между линией действия силы
- плечо - кратчайшее расстояние между линией действия силы  и точкой O.
и точкой O.

 Момент силы относительно оси z равен произведению момента инерции тела относительно этой оси на угловое ускорение - основной закон динамики вращательного движения.
Момент силы относительно оси z равен произведению момента инерции тела относительно этой оси на угловое ускорение - основной закон динамики вращательного движения. При одновременном действии на тело нескольких моментов сил основной закон динамики вращательного движения примет вид:
При одновременном действии на тело нескольких моментов сил основной закон динамики вращательного движения примет вид: .
. относительно неподвижной точки О (Рисунок 20)называется векторная физическая величина, определяемая векторным произведением
относительно неподвижной точки О (Рисунок 20)называется векторная физическая величина, определяемая векторным произведением  .
.
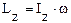



 , где uс - скорость центра масс,
, где uс - скорость центра масс, .
. , где m – масса системы
, где m – масса системы  , mi – масса i-той частицы,
, mi – масса i-той частицы, 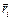 - радиус - вектор i-той частицы.
- радиус - вектор i-той частицы. ;
; 
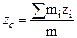

 .
○ 2. …
.
○ 2. …  .
○ 3. …|
.
○ 3. …|  .
○ 4. …
.
○ 4. …  Точка 4.
Точка 4.
 …F^R.
○ 5. …Fh.
…F^R.
○ 5. …Fh.
 Сплошной диск 1 и тонкое кольцо 2 одинаковых масс и радиусов исходно неподвижны. Их начинают синхронно (с одинаковыми угловыми ускорениями) раскручивать вокруг осей симметрии моментами сил M1 и M2 соответственно. Чему равно отношение величин этих моментов M1/M2?
Сплошной диск 1 и тонкое кольцо 2 одинаковых масс и радиусов исходно неподвижны. Их начинают синхронно (с одинаковыми угловыми ускорениями) раскручивать вокруг осей симметрии моментами сил M1 и M2 соответственно. Чему равно отношение величин этих моментов M1/M2?
 Запишите значение
Запишите значение
 - векторная (геометрическая) сумма всех сил равна 0. При решении задачэто условие обычно записывается в виде проекций на координатные оси х и у:
- векторная (геометрическая) сумма всех сил равна 0. При решении задачэто условие обычно записывается в виде проекций на координатные оси х и у: 
 .
.
 где
где  - векторная сумма моментов сил, действующих на АТТ. Из этого уравнения следует второе условие равновесия АТТ:
- векторная сумма моментов сил, действующих на АТТ. Из этого уравнения следует второе условие равновесия АТТ:  - векторная сумма моментов сил относительно любой оси должна быть равна 0. Для плоской системы сил
- векторная сумма моментов сил относительно любой оси должна быть равна 0. Для плоской системы сил  . Моменту сил, стремящихся повернуть тело относительно оси z по часовой стрелке присваивается знак "+", против - знак "–".
. Моменту сил, стремящихся повернуть тело относительно оси z по часовой стрелке присваивается знак "+", против - знак "–". - постоянная величина, где R - радиус орбиты планеты (половина большой оси эллипса);
- постоянная величина, где R - радиус орбиты планеты (половина большой оси эллипса);  , где:
, где: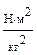
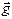 под действием силы тяжести
под действием силы тяжести  .
. 
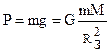 , где М - масса Земли, m - масса тела, R3 - радиус Земли. Отсюда:
, где М - масса Земли, m - масса тела, R3 - радиус Земли. Отсюда: 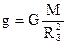
 . Таким образом, сила тяжести уменьшается с удалением от Земли.
. Таким образом, сила тяжести уменьшается с удалением от Земли.
 Если тело массой
Если тело массой  до расстояния
до расстояния 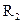 (рисунок 24), то работа по его перемещению:
(рисунок 24), то работа по его перемещению: 
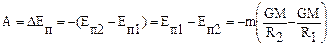
 ®0.
®0.
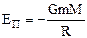 .
.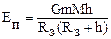 , где
, где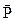 , но и другая сила
, но и другая сила 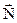 , создающая ускорение тела
, создающая ускорение тела 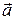 , то дополнительная сила
, то дополнительная сила 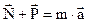 .
. =
=  .
.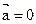 и
и 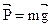 .
.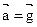 и
и 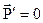 - тело будет невесомым.
- тело будет невесомым.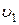 - это минимальная скорость тела, при которой оно становится спутником Земли и начинает двигаться вокруг Земли по круговой орбите радиусом
- это минимальная скорость тела, при которой оно становится спутником Земли и начинает двигаться вокруг Земли по круговой орбите радиусом 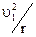 . По второму закону Ньютона
. По второму закону Ньютона 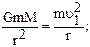
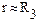 ;
; 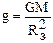 и
и  .
.
 - скорость, при которой тело преодолевает притяжение Земли и превращается в спутник Солнца. Для этого необходимо, чтобы кинетическая энергия тела была равна работе, совершаемой против сил тяготения.
- скорость, при которой тело преодолевает притяжение Земли и превращается в спутник Солнца. Для этого необходимо, чтобы кинетическая энергия тела была равна работе, совершаемой против сил тяготения.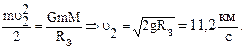
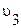 - позволяет телу покинуть Солнечную систему, преодолев притяжение Солнца.
- позволяет телу покинуть Солнечную систему, преодолев притяжение Солнца.  = 16,7
= 16,7 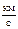 при условии запуска тела в направлении орбитального движения Земли. При запуске тела в противоположном направлении
при условии запуска тела в направлении орбитального движения Земли. При запуске тела в противоположном направлении 


