
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение МТ по прямой и по окружности
В случае прямолинейного движения МТ ускорение При равномерном прямолинейном движении МТ вдоль координаты В общем случае модуль перемещения МТ к моменту времени Для двухмерного пространства ХОY и прямолинейного равномерного движения МТ координаты МТ в любой момент времени
При равноускоренном прямолинейном движении МТ в двухмерном пространстве (при
Площадь под графиком (Рисунок 4), численно равная пройденному пути, является площадью трапеции:
Учитывая, что Перемещение может быть вычислено и по формуле: Координаты МТ в двухмерном пространстве вычисляются по формулам:
При равномерном движении МТ по окружности (рисунок 7) радиус-вектор
Отношение Пусть радиус-вектор совершит один полный оборот, т.е. повернется на угол Dj = 2p за время Dt = Т. Время Т одного полного оборота МТ называется периодом вращения. Таким образом: Частота вращения Один Герц – это частота, при которой МТ совершает один полный оборот за 1 секунду. Угол поворота в радианах Модуль линейной скорости МТ, вращающейся по окружности с радиусом
Ускорение МТ при равномерном движении по окружности (Рисунок 8) можно определить следующим образом: так как модуль скорости не меняется, то ускорение меняет только направление вектора скорости, т.е. является нормальным
DАВС - равнобедренный. Угол между
При малом времени Dt длина дуги DS мало отличается от Модуль среднего ускорения: Модуль мгновенного ускорения:
В этом выражении v – частота вращения. Контрольные вопросы: 1. Как направлены векторы мгновенной скорости и ускорения при прямолинейном движении? 2. Как вычислить величину перемещения при равномерном прямолинейном движении? 3. Как вычислить модуль скорости при равнопеременном прямолинейном движении? 4. Как вычислить путь при равнопеременном прямолинейном движении? 5. Что такое угловая скорость и как она связана с периодом вращения и линейной скоростью МТ? 6. Как направлено ускорение при равномерном движении МТ по окружности? 7. Как вычислить ускорение при равномерном движении МТ по окружности? Движение материальной точки при действии гравитации На практике весьма распространена задача по определению параметров движения тела при действии гравитации (Рисунок 9). В общем виде задача формулируется следующим образом: Тело бросили с высоты h над поверхностью Земли, сообщив ему начальную скорость
- зависимость координат тела от времени; -время движения и время подъема; -дальность полета; -максимальную высоту подъема тела над поверхностью Земли; -уравнение траектории.
Пусть траектория тела находится в плоскости ХОУ. У поверхности Земли все тела движутся с постоянным ускорением
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 988; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.014 с.) |
 .
. (
(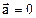 ,
,  ) модуль скорости:
) модуль скорости:  . Здесь
. Здесь  - координата МТ в начальный момент времени. Эту координату называют начальным условием. Если отсчет времени начинается от 0 (
- координата МТ в начальный момент времени. Эту координату называют начальным условием. Если отсчет времени начинается от 0 ( ), то
), то  . Отсюда координата МТ в момент
. Отсюда координата МТ в момент  :
:  .
. .
. вычисляются по формулам:
вычисляются по формулам:
 , где
, где  и
и  - начальные условия (координаты МТ при времени
- начальные условия (координаты МТ при времени  );
); - проекции вектора скорости
- проекции вектора скорости 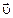 на оси
на оси  и
и 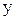 ;
; 
 ) и начальных условиях:
) и начальных условиях:  ,
,  проекции скорости на координаты
проекции скорости на координаты 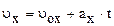 ;
; .
.

 .
. получим, что перемещение при равнопеременном движении:
получим, что перемещение при равнопеременном движении:  .
.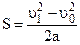 .
. ;
;  .
. Движение МТ по окружности с постоянной по модулю скоростью
Движение МТ по окружности с постоянной по модулю скоростью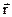 описывает за равные промежутки времени Dt равные углы Dj.
описывает за равные промежутки времени Dt равные углы Dj.
 называется средней угловой скоростью.. При равномерном движении МТ по окружности
называется средней угловой скоростью.. При равномерном движении МТ по окружности  =const и
=const и  . Размерность угловой скорости:
. Размерность угловой скорости: 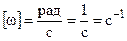 .
. , где:
, где: - это число оборотов в 1 секунду. Размерность частоты -
- это число оборотов в 1 секунду. Размерность частоты - 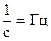 (герц)
(герц) , где
, где  - длина дуги, а
- длина дуги, а 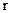 - радиус окружности.
- радиус окружности. . Т.к.
. Т.к. 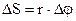 , то
, то  .
.



 и
и 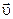 в пределе стремится к
в пределе стремится к  , а ускорение
, а ускорение  направлено к центру окружности. Из подобия треугольников ОАD и АВС следует:
направлено к центру окружности. Из подобия треугольников ОАD и АВС следует:  .
. .
. .
. .
.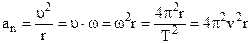
 под углом a к горизонту.
под углом a к горизонту.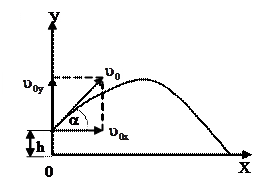 Определить:
Определить: В качестве тела отсчета выберем Землю. Начало системы координат поместим в точку О расположенную на поверхности Земли.
В качестве тела отсчета выберем Землю. Начало системы координат поместим в точку О расположенную на поверхности Земли. , направленным вертикально вниз. Поэтому ускорения
, направленным вертикально вниз. Поэтому ускорения  ,
, 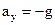 .
.


