
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следовательно, Движение вдоль оси X – равномерное и прямолинейное, так как ускорение вдоль оси X отсутствует, а Движение вдоль оси y – равнопеременное и меняет направление.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Начальные условия: х0 = 0, у0 = h,
Параметры движения тела вдоль оси X:
Параметры движения тела вдоль оси Y:
Из уравнения (1.3): уравнение траектории: Выражение (1.5) является уравнением параболы типа
Время подъема тела можно определить, приравняв нулю проекцию скорости uу в уравнении (1.2):
Подставив это время в уравнение (1.4), можно найти максимальную высоту подъема:
Приравняв в (1.4) нулю координату " у ", можно получить время движения тела: Дальность полета
При h = 0:
В верхней точке траектории где R – радиус кривизны траектории в ее верхней точке. Контрольные вопросы: 1. Как формулируется задача движения МТ под действием тяготения? 2. Как направлены составляющие скорости в процессе движения МТ? 3. Расскажите алгоритм вычисления высоты подъема МТ. 4. Как найти дальность полета МТ?
Выберите правильные ответы на поставленные вопросы
Кинематика вращательного движения Абсолютно твердого тела Абсолютно твердым телом (АТТ) называется тело, которое ни при каких условиях не может деформироваться и при любых условиях расстояние между любыми двумя его точками остается постоянным. При вращении АТТ вокруг неподвижной оси (Рисунок 10) отдельные точки этого тела будут описывать окружности разных радиусов Быстрота вращения характеризуется углом Мгновенное значение угловой скорости Угловая скорость является векторной величиной

Поскольку направление угловой скорости выбрано произвольно, а сам вектор Средняя величина углового ускорения рассчитывается по формуле: Мгновенным угловым ускорением называется векторная величина, равная первой производной от угловой скорости по времени: Угловое ускорение тоже является псевдовектором. Если направление оси вращения не изменяется в пространстве, то векторы Модуль тангенциальной составляющей линейного ускорения вращающейся МТ, принадлежащей АТТ:

Модуль нормальной составляющей ускорения МТ:
где Длина пути, пройденного МТ по дуге окружности:
При равнопеременном вращении АТТ:
Плоское движение АТТ Плоским называется движение, при котором все точки тела движутся в параллельных плоскостях. Примером плоского движения является качение колеса без проскальзывания (Рисунок 11).
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.160 (0.008 с.) |

 ,
,  .
. = const!! (1.1)
= const!! (1.1) 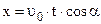 (1.3)
(1.3) (1.2)
(1.2) 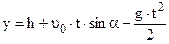 (1.4)
(1.4) подставим в (1.4) и получим
подставим в (1.4) и получим (1.5)
(1.5) .
.



 определяется из уравнения (1.3) при
определяется из уравнения (1.3) при  :
: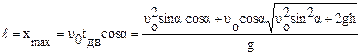
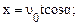
 ;
;


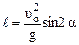 .
. ,
,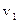 и
и 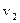 . Модуль скорости второй машины относительно первой равен:
○ 1. …v1.
○ 2. …v2.
○ 3. …v1-v2.
○ 4. …v2-v1.
○ 5. …v1+v2.
. Модуль скорости второй машины относительно первой равен:
○ 1. …v1.
○ 2. …v2.
○ 3. …v1-v2.
○ 4. …v2-v1.
○ 5. …v1+v2.

 50м.
50м.
 5. Все четыре тела прошли одинаковый путь.
5. Все четыре тела прошли одинаковый путь.
 50м.
50м.
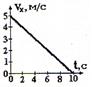
 1. 20 км/час. Х, км.
1. 20 км/час. Х, км.
 2. 40 км/час. 5
3. 60 км/час. 4
4. 75 км/час. 3
5. 90 км/час. 2
0 1 2 3 4 5
t, мин
2. 40 км/час. 5
3. 60 км/час. 4
4. 75 км/час. 3
5. 90 км/час. 2
0 1 2 3 4 5
t, мин
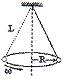
 ωL.
○ 5. ωR/L.
ωL.
○ 5. ωR/L.
 Колесо вращается с постоянной скоростью W в вертикальной плоскости и падает с ускорением g. В какой точке колеса ускорение минимально.
○ 1. (·)A
○ 2. (·)B
○ 3. (·)C
○ 4. (·)Д
Колесо вращается с постоянной скоростью W в вертикальной плоскости и падает с ускорением g. В какой точке колеса ускорение минимально.
○ 1. (·)A
○ 2. (·)B
○ 3. (·)C
○ 4. (·)Д
 ○ 2.
○ 2.  ○ 3.
○ 3.  ○ 4.
○ 4. 

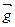 . В каких точках траектории тангенциальное ускорение положительно?
○ 1.
. В каких точках траектории тангенциальное ускорение положительно?
○ 1. 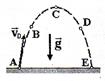 Во всех точках траектории.
○ 2. С.
○ 3. А и В.
○ 4. В и D.
○ 5. D и Е.
Во всех точках траектории.
○ 2. С.
○ 3. А и В.
○ 4. В и D.
○ 5. D и Е.
 , то чему равна угловая скорость при b=1м и t=10с?
Запишите значение и единицы измерения
, то чему равна угловая скорость при b=1м и t=10с?
Запишите значение и единицы измерения

 В точке А.
○ 2. В точке В.
○ 3. В точках С и D.
○ 4. В точках E и F.
○ 5. Во всех точках ускорение равно 0.
В точке А.
○ 2. В точке В.
○ 3. В точках С и D.
○ 4. В точках E и F.
○ 5. Во всех точках ускорение равно 0.
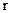 , центры которых лежат на оси вращения.
, центры которых лежат на оси вращения.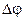 , на который поворачивается тело за единицу времени. При равномерном вращении
, на который поворачивается тело за единицу времени. При равномерном вращении  .
. .
.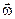 , характеризующей не только быстроту, но и направление вращения. Направлен вектор
, характеризующей не только быстроту, но и направление вращения. Направлен вектор 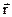

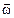 не имеет определенной точки приложения, то вектор
не имеет определенной точки приложения, то вектор  .
. .
. и
и  учитывая, что
учитывая, что  :
:
 ,
, - частота вращения
- частота вращения

 ;
;  , где:
, где: и
и  – начальные условия.
– начальные условия.


