
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 13. Движение материальной точки. Метод кинетостатикиСодержание книги
Поиск на нашем сайте
Иметь представление о свободных и несвободных материальных точках, о силах инерции, об использовании силы инерции для решения технических задач. Знать формулы для расчета силы инерции при поступательном и вращательном движениях, знать принцип Даламбера и уметь определять параметры движения с использованием законов динамики и метода кинетостатики. Свободная и несвободная точки
Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется свободной. Задачи решаются с помощью основного закона динамики. Материальные точки, движение которых ограничено связями, называются несвободными. Для несвободных точек необходимо определять реакции связей. Эти точки движутся под действием активных сил и ограничивающих движение реакций связей (пассивных сил). Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождаемости от связей). Сила инерции
Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел. Сила инерции — сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом. Рассчитано, что сила инерции равна FИН = / mа/
Таким образом, силы, действующие на материальные точки m1 и m2 (рис. 14.1), при разгоне платформы соответственно равны
Fин2 = m2 а
Разгоняющееся тело (платформа с массой т (рис. 14.1)) си При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального ап и касательного at (рис. 14.2). Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная
При равномерном движении по дуге всегда возникает нормальное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги (рис. 14.3).
Принцип кинетостатики (принцип Даламбера)
Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).
Даламбер предложил условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становится уравновешенной, и можно при решении задач динамики использовать уравнения статики.
Принцип Даламбера: Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии:
Порядок решения задач с использованием принципа Даламбера
Примеры решений задач
Решение Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре R. Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.

где Frb — движущая сила; Fтр – сила трения; G — сила тяжести; R — реакция опоры; Fmi — сила инерции; f — коэффициент трения. Пример 2. Тело весом3500 Н движется вверх по наклонной плоскости согласно уравнению S =0,16t2 (рис.14.5). Определить величину движущей силы, если коэффициент трения тела о плоскость f = 0,15. Решение 1. Составим расчетную схему, выберем систему координат с осью Ох вдоль наклонной плоскости. Активные силы: движущая, сила трения, сила тяжести. Наносим реакцию в опоре перпендикулярно плоскости. Чтобы верно направить силу инерции, необходимо знать направление ускорения, определить это можно по уравнению движения.
2. Определяем ускорение движения: a = v' = S"; v = S' = 0,32 t; a = v' = 0,32 м/с2 > 0. Силу Fин направим в обратную от ускорения сторону. 3. По принципу Даламбера составим уравнения равновесия:
4. Подставим все известные величины в уравнения равновесия:
Выразим неизвестную силу и решим уравнение:
Пример 3. График изменения скорости лифта при подъеме известен (рис. 14.6). Масса лифта с грузом 2800 кг. Определить натяжение каната, на котором подвешен лифт на всех участках подъема.
Решение 1. Рассмотрим участок 1 — подъем с ускорением. Составим схему сил (рис. 14.7). Уравнение равновесия кабины лифта:
где Т — натяжение каната; G — сила тяжести; FИH — сила инерции, растягивающая канат. Для определения ускорения на участке 1 учтем, что движение на этом участке равнопеременное, скорость v = vo + at; v0 = 0. Следовательно, ускорение:
Определяем усилие натяжения каната при подъеме с ускорением T1 = 2800(9,81 + 1,25) = 30968H; T1 = 30,97кН.
2. Рассмотрим участок 2 — равномерный подъем. Ускорение и сила инерции равны нулю. Натяжение каната равно силе тяжести. T2 – G = 0; Т2 = G = тg; Т2 = 2800 * 9,81 ≈ 28 кН. 3. Участок 3 — подъем с замедлением. Ускорение направлено в сторону, обратную направлению подъема. Составим схему сил (рис. 14.8). Уравнение равновесия: FИН3 + Т3 — G = 0. Отсюда Т3 = G — FHE3 = mg — ma 3. Ускорение (замедление) на этом участке определяется с учетом того, что v = 0. + п 5 / 2 ^о + оз^з = 0; а3 = - —; а3 = -- м/с. £3 b - Натяжение каната при замедлении до остановки: Т3 = 2 800 ^9,81 - 0 = 25 144 Н; Г3 - 25,14 кН. Таким образом, натяжение каната меняется при каждом подъеме и опускании, канат выходит из строя в результате усталости материала. Работоспособность зависит от времени.
Пример 4. Самолет выполняет «мертвую петлю» при скорости 160 м/с2, радиус петли 1000 м, масса летчика 75 кг. Определить величину давления тела на кресло в верхней точке «мертвой петли».
1. Схема сил, действующих на летчика (рис. 14.9): где G — сила тяжести, R — реакция в опоре, FИНп — сила инерции. Сила давления летчика на кресло равна силе давления опоры на летчика. Уравнение равновесия (движение равномерное по дуге, действует только нормальное ускорение): F"H — G — R = 0;
Решение
Активной силой, действующей на рамку, является сила тяжести груза
Освободив^ рамку от связей, прикладываем к ней реакции опор VА и VВ (рис. 1.61,6). Мысленно остановив рамку, прикладываем к ней в точке крепления груза центробежную силу инерции
Так как рамка вращается равномерно, касательное ускорение груза равно нулю и полное его ускорение равно нормальному. Соответственно полная сила инерции равна центробежной силе инерции груза. Нормальное ускорение направлено к оси вращения, сила инерции — противоположно (рис. 1.61,6).
Определим величину нормального ускорения: Сила инерции
Сила инерции и сила тяжести в заданном положении груза суммируются:
В данном случае сила тяжести значительно меньше силы инерции и, вообще говоря, можно было бы силой тяжести пренебречь. Составляя уравнения равновесия
находим
Решение
Добавочные динамические реакции V А и V в опор балки возникнут от силы инерции груза
Сила инерции направлена вниз, так как ускорение груза направлено вверх. Освобождаем балку от связей и заменяем их действие реакциями V А и V в. Составляем уравнения равновесия:
Решая уравнения, находим:
Контрольные вопросы и задания
1. Объясните разницу между понятиями «инертность» и «сила инерции».
2.
3. В чем заключается принцип кинетостатики?
4. Задано уравнение движения материальной точки S = 8,6 t 2. Определите ускорение точки в конце десятой секунды движения.
5. Тело движется вниз по наклонной плоскости (рис. 14.10). Нанесите силы, действующие на тело; используйте принцип Даламбера, запишите уравнение равновесия.
6.
7. Автомобиль въезжает на арочный мост с постоянной скоростью v (рис. 14.12). Нанесите силы, действующие на автомобиль в середине моста, используя принцип кинетостатики, запишите уравнения равновесия.
8. Ответьте на вопросы тестового задания.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 6652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.132 (0.008 с.) |



 лу инерции не воспринимает, иначе разгон платформы вообще был бы невозможен.
лу инерции не воспринимает, иначе разгон платформы вообще был бы невозможен.


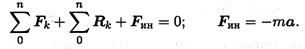
 Пример 1. Рассмотрим движение платформы по шероховатой поверхности с ускорением (рис. 14.4).
Пример 1. Рассмотрим движение платформы по шероховатой поверхности с ускорением (рис. 14.4).
 При а > 0 движение равноускоренное.
При а > 0 движение равноускоренное.

 Fдв = 3500 • 0,5 + 0,15 * 3500 • 0,866 + 3500 • 0,32 / 9,81 = 2318,8 Н.
Fдв = 3500 • 0,5 + 0,15 * 3500 • 0,866 + 3500 • 0,32 / 9,81 = 2318,8 Н.



 Пример 5. Жесткая рамка с грузом G массой т = 10 кг равномерно вращается с частотой n = 1200 об/мин (рис. 1.61, а). Определить реакции опор при нижнем (показанном на рисунке) положении груза. Массу рамки не учитывать.
Пример 5. Жесткая рамка с грузом G массой т = 10 кг равномерно вращается с частотой n = 1200 об/мин (рис. 1.61, а). Определить реакции опор при нижнем (показанном на рисунке) положении груза. Массу рамки не учитывать.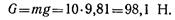



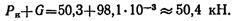

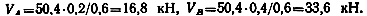
 Пример 6. По подкрановой балке (рис.1.62) перемещается тельферная тележка, грузоподъемность которой m = 104 кг. Определить добавочные динамические реакции опор балки при указанном на рисунке положении тележки, если тележка поднимает максимальный груз с ускорением а = 6,5 м/с2.
Пример 6. По подкрановой балке (рис.1.62) перемещается тельферная тележка, грузоподъемность которой m = 104 кг. Определить добавочные динамические реакции опор балки при указанном на рисунке положении тележки, если тележка поднимает максимальный груз с ускорением а = 6,5 м/с2.


 К каким телам приложена сила инерции, как направлена и по какой формуле может быть рассчитана?
К каким телам приложена сила инерции, как направлена и по какой формуле может быть рассчитана? Лифт спускается вниз с ускорением (рис. 14.11). Нанесите силы, действующие на кабину лифта, используя принцип кинетостатики, запишите уравнения равновесия.
Лифт спускается вниз с ускорением (рис. 14.11). Нанесите силы, действующие на кабину лифта, используя принцип кинетостатики, запишите уравнения равновесия.


