
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 15. Общие теоремы динамикиСодержание книги
Поиск на нашем сайте Иметь представление о понятиях «импульс силы», «количество движения», «кинетическая энергия»; о системе материальных точек, о внутренних и внешних силах системы. Знать основные теоремы динамики, основные уравнения динамики при поступательном и вращательном движениях твердого тела, формулы для расчета моментов инерции некоторых однородных твердых тел. Уметь определять параметры движения с помощью теорем динамики. Теорема об изменении количества движения
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость mv. Вектор количества движения совпадает по направлению с вектором скорости. Единица измерения \mv\ = кг*м/с. Произведение постоянного вектора силы на некоторый промежуток времени, в течение которого действует эта сила, называется импульсом силыF t. Вектор импульса силы по направлению совпадает с вектором силы.
Проинтегрируем обе части равенства:
Полученное соотношение выражает теорему об изменении количества движения точки:
Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени. Теорема об изменении кинетической энергии
Энергией называется способность тела совершать механическую работу.
Существуют две формы механической энергии: · потенциальная энергия, или энергия положения, и · кинетическая энергия, или энергия движения.
Потенциальная энергия (П) определяет способность тела совершать работу при опускании с некоторой высоты до уровня моря. Потенциальная энергия численно равна работе силы тяжести. П = Gh, где h — высота точки над уровнем моря.
Кинетическая энергия (К) определяется способностью движущегося тела совершать работу. Для материальной точки кинетическая энергия рассчитывается по формуле
Кинетическая энергия — величина скалярная, положительная. Единицы измерения:
Запишем для материальной точки (рис. 17.2) основное уравнение движения
Спроектируем обе части векторного равенства на направление скорости:
Известно, что
Откуда
Умножив обе части полученного выражения на некоторое перемещение dS, получим :
Полученное равенство выражает теорему об изменении кинетической энергии точки:
Изменение кинетической энергии на некотором пути равно работе всех действующих на точку сил на том же пути. Основы динамики системы материальных точек
Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.
Любое материальное тело в механике рассматривается как механическая система, образуемая совокупностью материальных точек. Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения остальныхточек. Силы, действующие на точки системы, делятся на · внешние и · внутренние. Силы взаимодействия между точками этой системы называют внутренними. К внешним силам относятся силы, действующие со стороны точек, не входящих в эту систему. Примерами внешних сил являются сила тяжести, сила давления, сила трения и др. К внутренним силам относятся силы упругости. Движение механической системы зависит не только от внешних сил, но и от суммарной массы системы
Движение системы зависит и от положения центра масс системы — условной точки, в которой сосредоточена вся масса тела. Обычно считают, что в центре масс приложены все внешние силы. Движение центра масс определяет движение всей системы только при поступательном движении, при котором все точки тела движутся одинаково.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |


 Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).
Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).



 Энергия имеет размерность работы.
Энергия имеет размерность работы.




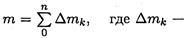 масса отдельных точек механической системы.
масса отдельных точек механической системы.


