Решение задач на равновесие геометрическим способом

 

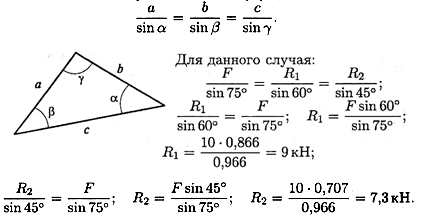
Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).

Порядок решения задач:

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу кон­тура.)

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения решения рекомендуется определить величины, векторов (сторон многоугольника) с помощью геометрических зави­симостей.

Пример 1. Груз подвешен на стержнях и находится в равнове­сии. Определить усилия в стержнях (рис. 2.5, а).

Решение

1. Усилия, возникающие в стержнях крепления, по величине рав­ны силам, с которыми стержни поддерживают груз (5-я аксиома ста­тики) (рис. 2.5, а).

 

Определяем возможные направления реакций связей «жесткие стержни».

. γ = 180⁰ – 60⁰ – 45⁰

Усилия направлены вдоль стержней.

2. Освободим точку А от связей, заменив действие связей их реакциями (рис. 2.5, б).

3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в неко­тором масштабе.

Из концов вектора F проводим линии, параллельные реакциям и R₁ и R₂.

Пересекаясь, линии создадут треугольник (рис. 2.5, в). Зная мас­штаб построений и измерив длину сторон треугольника, можно опре­делить величину реакций в стержнях.

 

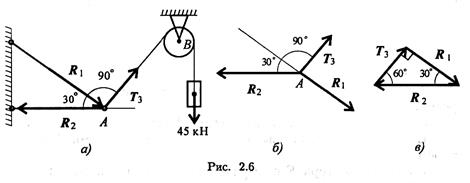
4. Для более точных расчетов можно воспользоваться геометри­ческими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная:

Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.

Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6, а).

Решение

 

1. Нанесем на схему возможные направления усилий, приложенных в точке А. Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки А к точке В.

2. Груз находится в равновесии, следовательно, в равновесии находится точка А, в которой пересекаются три силы.

Освободим точку А от связей и рассмотрим ее равновесие (рис. 2.6, б).

Замечание. Рассмотрим только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: Тз = 45 кН.

3. Строим треугольник для сил, приложенных в точке А, начиная с известной силы Т₃. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке А.

Образовался прямоугольный треугольник (рис. 2.6, е).

4. Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике:

Замечание. При равновесии векторы сил в треуголь­нике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 2.6, а. Направления совпали, следовательно, направления реакций определены верно.

Контрольные вопросы и задания

 

1. По изображенным многоугольникам сил (рис. 2.7) решите, сколько сил входит в каждую систему и какая из них уравновешена. (Обратить внимание на направление векторов.)

 

2. Из представленных силовых треугольников выберете тре­угольник, построенный для точки А (рис. 2.8, 2.9).

 

4.
Шар подвешен на нити и находится в равновесии. Обратить внимание на направление реакции от гладкой опоры и условие равновесия шара (рис. 2.8).

5. Груз F подвешен на канате и находится в равновесии. Обратить внимание на реакции, приложенные к точке А. Силы, не приложенные к точке А, не рассматриваются. Не забывать об условии равновесия системы сил (рис. 2.9).

 

ЛЕКЦИЯ 3

Тема 1.2. Плоская система сходящихся сил. Определение равнодействующей аналитическим способом

 

Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в ана­литической форме.

Уметь определять проекции силы на две взаимно перпендику­лярные оси, решать задачи на равновесие в аналитической форме.

Проекция силы на ось

 

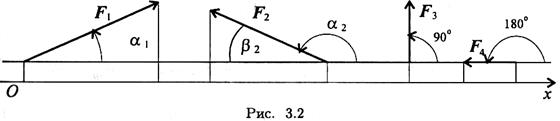
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным направ­лением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

F_1x = F₁ cos α₁ > 0; F_2x = F₂ cos α₂ = - F₂ cos β₂;

cos α₂ = cos (180° — β₂)= — cos β₂

F_3x = F₃ cos90° = 0; F_4x = F₄ cos180° = - F₄.

Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).