
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные кинематические параметрыСодержание книги
Поиск на нашем сайте
Траектория. Линию, которую очерчивает материальная точка при движении в пространстве, называют траекторией. Траектория может быть прямой и кривой, плоской и пространственной линией. Уравнение траектории при плоском движении: у = f(х).
Уравнение движения точки. Уравнение, определяющее положение движущейся точки в зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки, рассматриваемой как начало отсчета (рис. 9.1). Такой способ задания движения называется естественным. Таким образом, уравнение движения можно представить в виде S = f(t). Положение точки можно также определить, если известны ее координаты в зависимости от времени (рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения:
В случае пространственного движения добавляется и третья координата z = fз(t) Такой способ задания движения называют координатным.
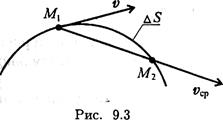
Скорость — вектор, в любой момент времени направленный по касательной к траектории в сторону направления движения (рис. 9.3). Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным. Средняя скорость на пути AS определяется как
где ΔS — пройденный путь за время Δt; Δt — промежуток времени. Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным. В этом случае скорость — величина переменная и зависит от времени v = f(t). При рассмотрении малых промежутков времени (Δt → 0) средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как производную пути по времени:
За единицу скорости принимают 1 м/с. Иногда скорость измеряют в км/ч, 1км/ч = 0,278м/с. Ускорение точки. Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.
При рассмотрении бесконечно малого промежутка времени среднее ускорение превратится в ускорение в данный момент:
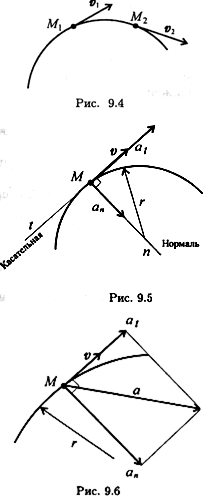
Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное (рис. 9.5). Нормальное ускорение ап характеризует изменение скорости по направлению и определяется как
где г — радиус кривизны траектории в данный момент времени. Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги. Касательное ускорение at характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости. Формула для определения касательного ускорения имеет вид:
Значение полного ускорения определяется как аt = d V/dt = v1 = S’’ (рис. 9.6). Примеры решения задач Пример 1. Дано уравнение движения точки: S = 0,36t2 + 0,18t. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые 3 секунды. Решение 1. Уравнение скорости
S' = 2 • 0,36t + 0,18; v = 0,72 t + 0,18. 2. Скорость в конце третьей секунды (t = Зс) v3 = 0,72 * 3 + 0,18 = 2,34м/с. 3.Средняя скорость Vср = dS/dt = (0,36 • 32+ 0,18 * 3)/3 = 1,26 м/с. Пример 2. Точка движется по кривой радиуса г = 10 м согласно уравнению S = 2,5 t2 + 1,2 t + 2,5 (рис. 9.6). Определить полное ускорение точки в конце второй секунды движения и указать направление касательной и нормальной составляющих ускорения в точке М. Решение 1. Касательное ускорение определяется как at = dV/dt Уравнение скорости: v = dS/dt Скорость будет равна v = 2 * 2,5t + 1,2; v = 5t + 1,2 (м/с). Касательное ускорение: аt = v' = 5 м/с2. Вывод: касательное ускорение не зависит от времени, оно постоянно. 2. Нормальное ускорение: ап = v2/r Скорость на второй секунде будет равна v2 = 5*2 + 1,2 = 11,2 м/с. Величина нормального ускорения: ап 2 = (11,2)2/10 = 12,54 м/с2. 3. Полное ускорение:
Полное ускорение в конце второй секунды:
4. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.
Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, т. к. касательное ускорение — положительная величина (скорость растет). Пример 3. По дуге, равной 1/4 длины окружности радиуса г = 16м (рис. 1.110), из положения А0 в положение A1 движется точка согласно уравнению s = πt2. Определить скорость точки в момент, когда она проходит середину длины дуги A0A1, и в момент достижения положения A1. Решение
1.
2. Из заданного уравнения движения s = πt2 находим, что точка после начала движения достигает середины дуги через промежуток времени
3. Продифференцировав уравнение движения, найдем уравнение скорости:
4. Подставив значение t = 2 с в уравнение скорости, найдем
5. Проводим в точке А (середину дуги A0A1) касательную к траектории и изобразим вектор скорости v (рис. 1.110). Скорость точки в конце траектории (в положении A1) рекомендуется найти самостоятельно. (Ответ: 17,8 м/с.)
Пример 4. Для точки, движение которой рассматривалось в примере 3, определить ускорения а и a1 соответственно для положений точки в А и A1. Решение
1. Точка движется согласно уравнению s = πt2; следовательно, v =2st и из формулы
2. Как известно из примера 1.19, в момент, когда точка занимает на траектории положение А, ее скорость v = 4π = 12,6 м/с. Следовательно, в этот момент значение нормального ускорения
3. Находим направление ускорения а точки в момент, когда она проходит положение A, используя третью из формул (рис. 1.113):
4. Находим модуль ускорения точки, используя первую из формул (1.90):
Рекомендуется самостоятельно проверить полученный результат по формуле (1.89), а затем найти модуль и направление ускорения точки в положении (Ответ: at=20,8 м/с2; а1«72°30'.)
Контрольные вопросы и задания
1. Запишите в общем виде закон движения в естественной и координатной форме. 2. Что называют траекторией движения? 3. Как определяется скорость движения точки при естественном способе задания движения? 4. Запишите формулы для определения касательного, нормального и полного ускорений. 5. Что характеризует касательное ускорение и как оно направлено по отношению к вектору скорости? 6. Что характеризует и как направлено нормальное ускорение?
ЛЕКЦИЯ 10 Тема 1.8. Кинематика точки
Иметь представление о скоростях средней и истинной, об ускорении при прямолинейном и криволинейном движениях, о различных видах движения точки. Знать формулы (без вывода) и графики равномерного и равнопеременного движений точки. Уметь определять параметры движения точки по заданному закону движения, строить и читать кинематические графики.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 5091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.42 (0.01 с.) |

 Пройденный путь. Путь измеряется вдоль траектории в направлении движения. Обозначение — S, единицы измерения — метры.
Пройденный путь. Путь измеряется вдоль траектории в направлении движения. Обозначение — S, единицы измерения — метры. 
 Скорость движения. Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.
Скорость движения. Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.

 Скорость точки при перемещении из точки М1 в точку М2 меняется по величине и направлению. Среднее значение ускорения за этот промежуток времени
Скорость точки при перемещении из точки М1 в точку М2 меняется по величине и направлению. Среднее значение ускорения за этот промежуток времени


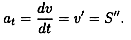



 Если длина дуги А0А1 равна 1/4 длины окружности, то середина дуги А находится от начала отсчета А0 на расстоянии 1/8 окружности, т, е.
Если длина дуги А0А1 равна 1/4 длины окружности, то середина дуги А находится от начала отсчета А0 на расстоянии 1/8 окружности, т, е.




 модуль касательного ускорения от времени не зависит, значит при любом положении точки на траектории ее касательное ускорение at = 6,28 м/с2.
модуль касательного ускорения от времени не зависит, значит при любом положении точки на траектории ее касательное ускорение at = 6,28 м/с2.





