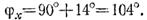Условие равновесия произвольной плоской системы сил

 

1. При равновесии главный вектор системы равен нулю (Fгл = 0).

Аналитическое определение главного вектора приводит к выводу:

 

где Fk_x и Fk_y — проекции векторов на оси координат.

2. Поскольку точка приведения выбрана произвольно, ясно, что при равновесии сумма моментов сил системы относительно любой точки на плоскости должна равняться нулю:

где А и В — разные точки приведения.

Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и доста­точно, чтобы алгебраическая сумма проекций всех сил системы на любую ось относительно любой точки в плоскости действия сил равнялась нулю.

Получим основную форму уравнения равновесия:

 

Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно соста­вить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.

Таким образом, имеем пять независимых уравнений равновесия.

Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.

Для разных случаев используются три группы уравнений рав­новесия.

 

Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:

 

Ось Ох системы координат параллельна линии действия сил.

Примеры решения задач

 

Пример 1. Найти момент присоединенной пары при переносе силы F₃ в точку В (рис. 5.3). F ₁ = 10кН; F ₂ = 15кН; F₃ = 18кН; а = 0,2 м.

Решение

Используем теорему Пуансо.

M_B(F₃) = 18 • 0,2 = 3,6 кН*м.

Пример 2. Найти главный вектор системы (рис. 5.4). F₁ = 10кН; F₂ = 16кН; F₃ = 12кН; т = 60кН-м.

Решение

 

Главный вектор равен геометрической сумме сил:

Пример 3. Найти главный момент системы относительно точки В (использовать данные примера 2).

Решение

Главный момент равен алгебраической сумме моментов сил от­носительно точки приведения:

Пример 4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы.

F₁ = 10кН; F₂ = 16 кН.

Решение

Наносим оси координат и используем уравнения равновесия:

Пример 5. К двум точкам тела приложены четыре силы F₁ = F₂ = F₃ = F₄ = 5 Н, как показано на рис. 1.46, а. Привести эти силы к точке А, а затем найти их равнодействующую.

Решение

 

1. Центр приведения (точка А) задан. Поэтому примем точ­ку А за начало координат и проведем ось х вдоль отрезка АВ, а ось у — по линии действия силы F₁ (рис. 1.46, а).

2. Определим проекции сил на ось х: F₁x=0', F_2x=F₂=5 Н; F_3X= — F_s sin 30° = 5 sin 30° = —2,5 Н; F_4X = — F₄sin 60° = — 5 sin 60° = — 4,33 H.

Отсюда проекция на ось х главного вектора

 

3.Определим проекции сил на ось у:

F_1y = F₁ = 5 Н; F_{2Y =} 0; F_3Y =:F₃sm60° = 5 sin 60° = 4,33 H;

Отсюда проекция на ось у главного вектора

Для большей наглядности и облегчения дальнейшего решения задачи целесо­образно найденные проекции F_{гл х} и F_{гл у} главного вектора отложить вдоль осей координат (рис. 1.46, б).

4. Из формулы (1,27) определим модуль главного вектора:

5. Находим угол

По таблицам или с помощью счетной логарифмической линейки определяем Из рис. 1.46, б следует, что

 

6. Определяем главный момент, как алгебраическую сумму моментов данных сил относительно точки А М_А(F₁) = 0 и М_А(F₂) = 0, так как линия действия сил F₁ и F₂ проходит через точку А (центр приведения);

М_А(F₃) = F₃ l₃ = 5 * 2 * sin 60⁰ = 8,66 (H*м)

М_А(F₄) = -- F₄ l₄ = -- 5 * 2 * sin 30⁰ = -- 5 (H*м)

 

Главный момент M_ГЛ > 0, значит он действует против хода часовой стрелки (рис. 1.46, б).

Равнодействующая F_Σ = Fгл и линия ее действия, параллельная главному вектору, проходит от центра приведения А на расстоянии

(рис. 1.46, в).

Линия действия равнодействующей пересекает ось х в точке С и отсекает отрезок

Таким образом, равнодействующая заданной на рис. 1.46, а системы сил F_Σ = 7,07 Н, линия ее действия образует с выбранными осями координат углы φ_х = 104°, φ_у =14° и пересекает отрезок АВ в точке С на расстоянии АС = 54 см.

Тот же результат был бы получен при выборе за центр приведения точки В, но в этом случае получилось бы ВС₂ = 1,42 м и BС~ 146 см (рис, 1,46, б). Проверьте: так ли это.

 

 

Контрольные вопросы и задания

 

1. Чему равен главный вектор системы сил?

2. Чему равен главный момент системы сил при приведении ее к точке?

3. Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?

Выбрать из предложенных ответов:

· величиной;

· направлением;

· величиной и направлением;

· точкой приложения;

· ничем.

4. Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?

5. Тело вращается вокруг неподвижной оси. Чему равны главный вектор и главный момент действующей на него системы сил?

6. Найдите главный вектор и главный момент системы сил, если центр приведения находится в точке А (рис. 5.6).

 

 

7. Какое еще уравнение равновесия нужно составить, чтобы убе­диться в том, что система сил (рис. 5.7) находится в равновесии?

 

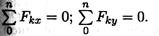
ЛЕКЦИЯ 6