
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как определить равнодействующую системы сходящихся сил?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
- Считая, что вектор силы скользящий, перенесем все силы данной системы вдоль линий действия в точку их пересечения и попарно сложим все силы методом параллелограмма. - Последовательно прикладываем вектора сил данной системы в конечную точку каждого последующего вектора, сохраняя его величину и направление, затем, соединив начало вектора 1 с концом вектора N, получим равнодействующую системы сходящихся сил. Такой метод называют методом силового много угольника. - Система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линии действия всех сил и равна их геометрической сумме. Запишите и сформулируйте условия равновесия системы сходящихся сил в векторной форме, а также в проекциях на оси декартовой системы координат. Условия равновесия в векторной форме - Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю.
- Если Условия равновесия в аналитической форме - - Сформулируйте теорему о трех уравновешенных силах. Если под действием трёх сил тело находиться в равновесии, и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пресекаются в одной точке. Дайте определение алгебраической величины момента силы относительно некоторого центра. Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.
Запишите векторное выражение момента силы относительно некоторого центра. Момент силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы.
Почему для плоской системы сил нет необходимости придавать векторный смысл моменту силы? - В случае плоской системы сил момент силы относительно точки можно принимать за алгебраическую величину. - Для пространственной системы сил, момент – это вектор, который направлен перпендикулярно к плоскости, в которой лежат сила и точка, в ту сторону, откуда вращение тела силой представляется происходящим против хода часовой стрелки. Дайте определение момента силы относительно оси и укажите способы его нахождения. - Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой плоскости с осью. - Момент силы относительно оси равен проекции на эту ось вектора момента силы относительно произвольной точки, лежащей на этой оси. - Если сила
- для определения знака момента, удобно рассматривать систему с положительных направления осей x, y, z и принимать момент положительным, если проекция силы на плоскость, перпендикулярную оси пытается создать вращательный эффект вокруг этой же оси против хода часовой стрелки. В каких случаях момент силы относительно оси равен нулю? Момент силы относительно оси равен нулю, когда линия действия силы параллельная оси или пересекает её.
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.103 (0.006 с.) |


 - вектор, замыкающий силовой многоугольник: геометрической условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.
- вектор, замыкающий силовой многоугольник: геометрической условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут. , т.е.
, т.е. 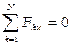 ,
, 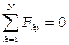 ,
,  . Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.
. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.
 задана своими проекциями
задана своими проекциями  и координатами x, y, z точки приложения, то момент силы относительно начала координат может быть представлен в виде определителя третьего порядка:
и координатами x, y, z точки приложения, то момент силы относительно начала координат может быть представлен в виде определителя третьего порядка:



