
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напишите и сформулируйте условия равновесия произвольной пространственной системы сил в векторной и аналитической формах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
- Запишем условие равновесия в векторной форме:
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы относительно произвольно выбранного центра приведения равнялись нулю. - Запишем условие равновесия в аналитической форме:
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраические суммы проекций сил на каждую из 3-х осей координат и алгебраические суммы моментов проекций сил на плоскости, перпендикулярные осям относительно точек пересечения этих осей с плоскостями равнялись нулю. Напишите и сформулируйте условия равновесия пространственной системы параллельных сил. Для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и сумма моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю.
Сформулируйте необходимые и достаточные условия равновесия произвольной плоской системы сил? - для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы проекций этих сил на каждую их двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равная нулю.
- для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трёх точек, не лежащих на одной прямой, были равны нулю.
- для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно двух любых точек А и В и сумма проекция на ось Ох, не перпендикулярную прямой, проходящей через точки А и В/, были ранвы нулю.
Напишите и сформулируйте три формы условий равновесия произвольной плоской системы сил. См. вопр. 24
25. Какие статические инварианты Вам известны? - Величины, которые не изменяются при каком-либо преобразовании, называются инвариантами по отношению к этим преобразованиям. - Величина и направление главного вектора не зависит от выбора центра приведения.
- Скалярное произведение главного момента произвольной пространственной системы сил на главный вектор той же системы не зависит от выбора центра приведения и является вторым инвариантом.
26. Каков геометрический смысл второго инварианта. Второй инвариант – это проекция главного момента на направление главного вектора системы, то есть он является наименьшим главным моментом системы сил.
Как изменяется главный момент системы сил при изменении центра приведения? Главный момент системы сил относительно нового центра приведения Сл1: Если главный вектор данной системы сил равен нулю, то главный момент не зависит от выбора центра приведения. Сл2: Если главный вектор равен нулю и существует точка, относительно которой главный момент равен нулю, то главный момент будет равен нулю относительно любого другого центра приведения. Сл3: Главный момент данной системы сил одинаков для всех точек прямой, параллельной главному вектору.
Какая совокупность сил называется динамическим винтом. Совокупность силы, равной главному вектору, и пары сил с моментом, равным главному моменту, коллинеарным главному вектору, называется динамическим винтом или динамой.
Как должны быть взаимно расположены главный вектор и главный момент системы сил для того, чтобы она приводилась к динамическому винту? См. вопр. 29
Как должны быть взаимно расположены главный вектор и главный момент системы сил для того, чтобы она приводилась к равнодействующей? - Равнодействующая не проходит через центр: главный вектор и главный момент взаимно перпендикулярны. - Равнодействующая в центре приведения: главный момент равен нулю.
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.97.20 (0.01 с.) |

 и
и 
 ;
; 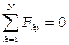 ;
; 
 ;
;  ;
; 

 и
и  и
и 
 - первый инвариант
- первый инвариант
 равен сумме главного момента относительно старого центра приведения
равен сумме главного момента относительно старого центра приведения  и момента главного вектора относительно нового центра в предположении, что он приложен в старом центре
и момента главного вектора относительно нового центра в предположении, что он приложен в старом центре 


