
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения равновесия системы силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, Mo=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
∑xi =0, ∑Mix=0; ∑yi =0, ∑Miy=0; (1.20) ∑zi =0, ∑Miz=0.
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три: ∑xi=0; ∑yi=0; (1.21) ∑Mo=0, причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия. Уравнения равновесия могут быть записаны иначе:
∑xi =0; ∑MA=0; (1.22) ∑MB=0.
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
∑MA=0; ∑MB=0; (1.23) ∑MC=0.
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой. Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего. При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
∑xi =0; ∑Mo=0. (1.24)
Рисунок 1.26
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия: ∑zi =0; ∑Mix=0; (1.25) ∑Miy=0. Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
∑xi =0; ∑yi =0; (1.26) ∑zi =0
и два уравнения для плоской системы:
∑xi =0; ∑yi =0. (1.27)
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия. Вопрос 22 Общие сведения о колебаниях. Общие сведения о колебаниях Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Таким свойством повторяемости обладают, например, качания маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиоприемника и т. п. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т. д. В данной главе рассматриваются механические колебания. Колебания широко распространены в природе и технике. Во многих случаях они играют отрицательную роль. Колебания моста, возникающие из-за толчков, сообщаемых ему колесами поезда при прохождении через стыки рельсов, колебания (вибрации) корпуса корабля, вызванные вращением гребного винта, вибрации крыльев самолета — все эти процессы могут привести к катастрофическим последствиям. В подобных случаях задача заключается в том, чтобы предотвратить возникновение колебаний или во всяком случае воспрепятствовать тому, чтобы колебания достигли опасных размеров. Вместе с тем колебательные процессы лежат в самой основе различных отраслей техники. Так, например, на колебательных процессах основана вся радиотехника. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания. Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок либо она была выведена из положения равновесия. Примером могут служить колебания шарика, подвешенного на нити (маятник). Для того чтобы вызвать колебания, можно либо толкнуть шарик, либо, отведя в сторону, отпустить его. Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу. Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой — система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение. При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например длины нити, к которой подвешен шарик, совершающий колебания. Простейшими являются гармонические колебания, т. е. такие колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса. Этот вид колебаний осооенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническим, и, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний. Вопрос 22.1 Гармонические колебания.
Вопрос 22.2 Гармонический осциллятор. Систему, описываемую уравнением
Следовательно, гармонический осциллятор представляет собой систему, которая совершает гармонические колебания около положения равновесия. Для гармонического осциллятора справедливы все результаты, полученные ранее для гармонического колебания. Рассмотрим и обсудим ещё дополнительно к ним два вопроса. Найдем импульс гармонического осциллятора. Продифференцируем выражение
В каждом положении, характеризуемом отклонением “x”, осциллятор имеет некоторое значение ”p”. Чтобы найти ”p” как функцию ”x”, нужно исключить ”t” из написанных для ”p” и ”x” уравнений, Представим эти уравнения в виде:
Возведя эти выражения в квадрат и складывая, получим:
Найдем теперь площадь эллипса
Здесь Следовательно,
Таким образом, полная энергия гармонического осциллятора пропорциональна площади эллипса, причем коэффициентом пропорциональности служит собственная частота осциллятора. Вопрос 23
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 776; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.01 с.) |




 (1) где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ —начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий названиепериод колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
(1) где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ —начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий названиепериод колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.  откуда
откуда  (2) Величина, обратная периоду колебаний,
(2) Величина, обратная периоду колебаний, 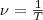 (3) т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
(3) т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем  Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса. Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса. Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания: 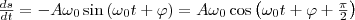 (4)
(4)  (5) т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).
(5) т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).
 Рис.1
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний
Рис.1
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний 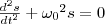 (6) (где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1). Гармонические колебания графически изображаются методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, которая выбрана на оси х, под углом φ, который равен начальной фазе колебания, откладывается вектор А, у которого модуль равен амплитуде А рассматриваемого колебания (рис. 2). Если данный вектор привести во вращение с угловой скоростью ω0, которая равна циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(ω0t+φ). Значит, гармоническое колебание можно представить как проекцию на некоторую выбранную произвольным образом ось вектора амплитуды А, который отложен из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
(6) (где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1). Гармонические колебания графически изображаются методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, которая выбрана на оси х, под углом φ, который равен начальной фазе колебания, откладывается вектор А, у которого модуль равен амплитуде А рассматриваемого колебания (рис. 2). Если данный вектор привести во вращение с угловой скоростью ω0, которая равна циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(ω0t+φ). Значит, гармоническое колебание можно представить как проекцию на некоторую выбранную произвольным образом ось вектора амплитуды А, который отложен из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
 Рис.2
В физике часто используется другой метод, отличающийся от метода вращающегося вектора амплитуды лишь по форме. В данном методе колеблющуюся величину представляют комплексным числом. Используя формулу Эйлера, для комплексных чисел
Рис.2
В физике часто используется другой метод, отличающийся от метода вращающегося вектора амплитуды лишь по форме. В данном методе колеблющуюся величину представляют комплексным числом. Используя формулу Эйлера, для комплексных чисел  (7) где
(7) где  - мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме:
- мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме:  (8) Вещественная часть формулы (8)
(8) Вещественная часть формулы (8)  есть гармоническое колебание. Обозначение Re вещественной части условимся опускать и (8) записывать в форме
есть гармоническое колебание. Обозначение Re вещественной части условимся опускать и (8) записывать в форме  В теории колебаний уславливаются, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
В теории колебаний уславливаются, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
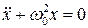 , где
, где  , будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид:
, будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид: .
. по t и, умножив полученный результат на массу осциллятора, получим:
по t и, умножив полученный результат на массу осциллятора, получим: . (8.8)
. (8.8) (8.9)
(8.9) . (8.10)
. (8.10) Нарисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·w0”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t¢ x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].
Нарисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·w0”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t¢ x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].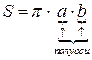 . Или
. Или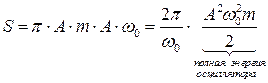 .
. , где n0 – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной.
, где n0 – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной. . Откуда
. Откуда . (8.11)
. (8.11)


