
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые случаи вычисления работы.Содержание книги
Поиск на нашем сайте
1) Работа сил тяжести, действующих на систему. Работа силы тяжести, действующей на частицу весом
где Р - вес системы, 2) Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.4) будет равна
так как Но, как легко видеть, Следовательно, в рассматриваемом случае элементарная работа равна произведению вращающего момента на элементарный угол поворота. Формула справедлива и при действии нескольких сил, если считать
Рис.4 При повороте на конечный угол
а в случае постоянного момента (Mz=const)
Если на тело действует пара сил, лежащая в плоскости, перпендикулярной к оси Оz, то Мz будет, очевидно, означать момент этой пары. Работа, затрачиваемая на изменение скорости вращения, равна изменению кинетической энергии тела:
Укажем еще, как в данном случае определяется мощность
Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощности вращающий момент будет тем больше, чем меньше угловая скорость. Если тело катится по горизонтальной поверхности, его кинетическая энергия будет складываться из энергии поступательного движения и энергии вращения (рис.5):
Рис.5 3) Работа сил трения, действующих на катящееся тело. На колесо радиуса R (рис.6), катящееся по некоторой плоскости (поверхности) без скольжения, действует сила трения F, препятствующая скольжению точки касания В вдоль плоскости. Элементарная работа этой силы
Рис.6
Следовательно, при качении без скольжения, работа силы трения, препятствующей скольжению, на любом перемещении тела равна нулю. По той же причине в этом случае равна нулю и работа нормальной реакции N, если считать тела недеформируемыми и силу N приложенной в точке В (как на рис.6, а). Сопротивление качению, возникающее вследствие деформации поверхностей (pис.6,б), создает пару (
где Если N= const, то полная работа сил сопротивления качению будет равна
Так как величина k/R мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать. Вопрос 18 Понятие об энергии. Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии. Энергия характеризует способность тела совершать работу.
Вопрос 18.1 Закон сохранения механической энергии Закон сохранения механической энергии Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
Следовательно
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.008 с.) |

 , будет равна
, будет равна  , где
, где  и
и  - координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна
- координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна
 - вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действующих на систему, вычисляется как работа их равнодействующей Р на перемещении центра тяжести (или центра масс) системы.
- вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действующих на систему, вычисляется как работа их равнодействующей Р на перемещении центра тяжести (или центра масс) системы. ,
,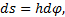 где
где 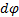 - угол поворота тела.
- угол поворота тела. . Будем называть величину
. Будем называть величину 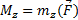 вращающим моментом. Тогда получим:
вращающим моментом. Тогда получим:  .
. .
.
 работа будет равна
работа будет равна
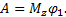




 . Но точка В в данном случае является мгновенным центром скоростей и VB=0. Так как
. Но точка В в данном случае является мгновенным центром скоростей и VB=0. Так как  , то
, то  и для каждого элементарного перемещения dA=0.
и для каждого элементарного перемещения dA=0.
 ), момент которой M=kN, где k- коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса
), момент которой M=kN, где k- коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса  , получим:
, получим:
 - элементарное перемещение центра С колеса.
- элементарное перемещение центра С колеса.




