Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов динамики. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии. Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1 поясняет решение этой задачи.
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
Обратим внимание на то, что сила
Из этих соотношений следует:
Центростремительное ускорение в нижней точке создается силами
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
Прочность нити должна, очевидно, превышать это значение. Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач. В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды. Сила трения не является консервативной. Работа силы трения зависит от длины пути. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии. Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 2).
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии. Вопрос 19 Понятие об ударе. Уда́р толчок, кратковременное взаимодействие тел, при которомпроисходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующихтел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при которомвременем взаимодействия можно пренебречь. Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системысохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно,считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телумгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров илиупругих мячиков. Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частицнизких энергий. Это следствие принципов квантовой механики, запрещающей произвольные измененияэнергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутреннихстепеней свободы, то механическая энергия системы не меняется. Изменение механической энергии можеттакже быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако,учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение квантасвета. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новыхчастиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужноучитывать изменение системы. Абсолютно неупругий удар Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальныеплощадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярныкасательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело. Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения моментаимпульса, но не выполняется закон сохранения механической энергии. Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики. Реальный удар При реальном ударе макроскопических тел происходит деформация соударяющихся тел и распространениепо ним упругих волн, передающих взаимодействие от сталкивающихся границ по всему телу. Пустьсталкиваются одинаковые тела. Если c — скорость звука в теле, L — характерный размер каждого тела, товремя удара будет порядка t = 2 L / c. Множитель 2 соответствует распространению волны в прямом иобратном направлении. Соответственно, систему сталкивающихся тел можно считать замкнутой, еслиимпульс внешних сил за время t мал по сравнению с импульсами тел. Кроме того, само время t должно бытьдостаточно мало, в противном случае становится проблематично оценить потери энергии на деформации завремя удара (часть энергии всегда расходуется на внутреннее трение), а само описание сталкивающихся телстановится неполным из-за существенного вклада внутренних степеней свободы. Необходимо, чтобы вседеформации при ударе были существенно меньше, чем размеры тел.
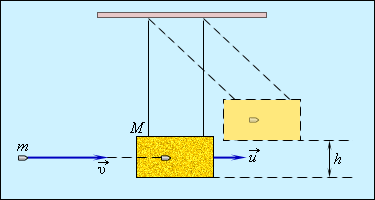
Вопрос 19.1 Определение скоростей тел при упругом и не упругом ударах примеры Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел. С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин. В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары. Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело. При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью Обозначим скорость ящика с застрявшей в нем пулей через
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами. При m << M Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2). Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
В общем случае массы m 1 и m 2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u 1 и u 2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u 1 и u 2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m 1 = m 2), первый шар после соударения останавливается (u 1 = 0), а второй движется со скоростью u 2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами). Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1 ' = υ1 – υ2. Определив по приведенным выше формулам скорости u 1 и u 2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
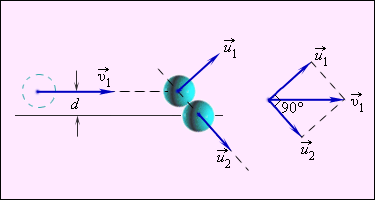
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой. Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей
Первое из этих равенств означает, что векторы скоростей Вопрос 20
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.118.36 (0.009 с.) |


 – сила натяжения нити в нижней точке траектории.
– сила натяжения нити в нижней точке траектории.

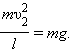

 направленными в противоположные стороны:
направленными в противоположные стороны:

 попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули. Тогда по закону сохранения импульса
Тогда по закону сохранения импульса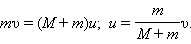


 почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M
почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M  – во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение
– во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение 




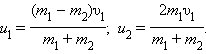


 и
и  после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости  налетающего шара. Если массы шаров одинаковы, то векторы скоростей
налетающего шара. Если массы шаров одинаковы, то векторы скоростей