Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи динамики материальной точки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Две основные задачи динамики точки В динамике точки решаются две основные задачи. Первая (прямая) задача динамики. По заданному движению, совершаемому точкой данной массы, требуется найти неизвестную действующую силу. Вторая (обратная) задача динамики. По заданным силам, действующим на точку данной массы, и заданным начальным условиям движения требуется найти закон движения точки. Это — основные (классические) задачи динамики точки, сформулированные самим основоположником динамики И. Ньютоном. С последующим развитием динамики появились новые задачи, сочетающие в себе черты обеих названных задач. Например, при несвободном движении точки реакции связей заранее неизвестны, и вторая задача приобретает смешанный характер — требуется найти как закон движения точки, так и реакции связей. Появились задачи об оптимальном движении, о движении точки с переменной массой и много других задач, тесно связанных с потребностями развивающейся техники. Основным математическим инструментом для решения задач динамики точки служат основное уравнение динамики и вытекающие из него дифференциальные уравнения движения. Вопрос 10 О силах в механике. Силы в механике Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях.
Вопрос10.1 Работа силы. Определение работы. Второй закон Ньютона в форме
Если угол между силой и перемещением обозначить через
Работа силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.
Поэтому для работы результирующей силы получаем
Итак, если на тело действует несколько сил, то полная работа (сумма работ всех сил) равна работе результирующей силы.
Tогда
Для работы силы получаем
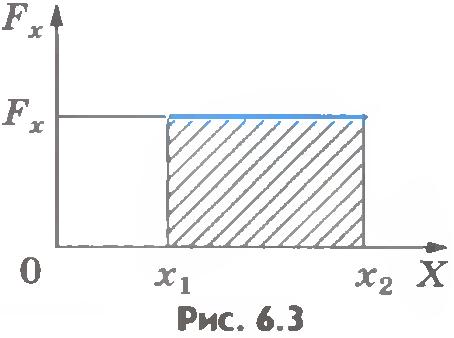
Очевидно, что площадь прямоугольника, заштрихованного на рисунке 6.3, численно равна работе при перемещении тела из точки с координатой x1 в точку с координатой x2.
Единица работы. Единицу работы можно установить с помощью основной формулы (6.2). Если при перемещении тела на единицу длины на него действует сила, модуль которой равен единице, и направление силы совпадает с направлением перемещения
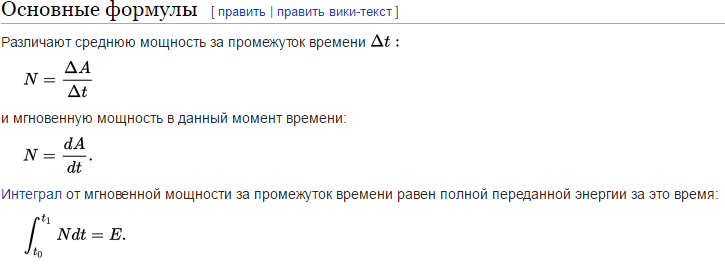
Итак, джоуль - это работа, совершаемая силой 1 Н на перемещении 1 м, если направления силы и перемещения совпадают. Вопрос 10.2 Мощность Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени
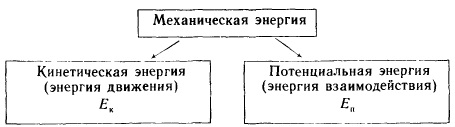
Вопрос 10.3 Энергия Энергия, изучаемая в механике, называется механической. Именно с нее мы и начнем знакомство с этим важнейшим понятием. Механическая энергия обозначается буквой Е и измеряется в тех же единицах, что и работа, т.е. в джоулях (Дж). Поскольку в механике изучают движение тел и их взаимодействие друг с другом, то принято различать два вида механической энергии - энергию, обусловленную движением тел, и энергию, обусловленную их взаимодействием. Первая из них обозначается Еk и называется кинетической энергией, вторая обозначается Еп и называется потенциальной энергией. Для расчета и той и другой энергии существует общее правило. Чтобы определить энергию, которой обладает тело, надо найти работу, необходимую для перевода этого тела из нулевого состояния в данное ( нулевое состояние - это то, в котором соответствующая энергия тела считается равной нулю). Чем больше эта работа, тем большей энергией обладает тело в данном состоянии. Воспользуемся этим правилом для расчета каждой из энергий. 1. К и н е т и ч е с к а я э н е р г и я. Найдем кинетическую энергию тела массой т, движущегося со скоростью, равной и. Кинетическая энергия - это энергия, обусловленная движением. Поэтому нулевым состоянием для нее является то, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем и его кинетическую энергию. Воспользовавшись определением работы (А = Fs), вторым законом Ньютона (F = mа), а также формулами (2.1) и (4.2), получаем (рис. 25) 2. П о т е н ц и а л ь н а я э н е р г и я. Найдем потенциальную энергию тела, взаимодействующего с Землей. Нулевым будем считать положение тела на поверхности Земли. Тогда потенциальная энергия тела, находящегося на некоторой высоте h, будет равна работе, необходимой для перемещения этого тела с поверхности Земли на заданную высоту. При равномерном подъеме, когда прикладываемая к телу сила совпадает по величине с силой тяжести (рис. 26), эта работа может бытьнайдена следующим образом: Это и есть потенциальная энергия тела на высоте h: Итак, потенциальная энергия тела, взаимодействующего с Землей, равна произведению массы этого тела, ускорению свободного падения и высоты, на которой находится тело. За нулевое положение тела при расчете его потенциальной энергии необязательно выбирать то, которое расположено на поверхности Земли. Это может быть и уровень пола в помещении, и поверхность стола и т. д. Нулевое положение, от которого отсчитывает- ся высота тела к, выбирают произвольно, руководствуясь обычно лишь соображениями удобства и простоты. По формуле (14.2) находится потенциальная энергия тела, взаимодействующего с Землей. Потенциальная энергия других взаимодействий находится по другим формулам. От энергии, которой обладает тело, зависит работа, которую оно может совершить. Чем больше энергия тела, тем большая работа будет совершена при переходе тела из данного состояния в нулевое. Проиллюстрируем это простыми опытами. Возьмем составной желоб, имеющий наклонную и горизонтальную части, и поместим на его сгибе алюминиевый цилиндр (рис. 27). Пуская по наклонной части желоба шарики разной массы с одинаковой высоты и шарики одинаковой массы с разных высот, можно заметить, что, чем большей потенциальной энергией наверху желоба и кинетической энергией внизу обладал шарик, тем на большее расстояние он передвинет металлический цилиндр. Вопрос 11 Механическая система. Механическая система Материальная точка является одной из основных моделей материальных тел в динамике. Однако во многих случаях ее недостаточно, поэтому наряду с материальной точкой в динамике рассматривают более общую модель — систему материальных точек. Системой материальных точек или механической системой называется выделенная каким-либо образом совокупность материальных точек. Вопрос 11.1 Движение системы кроме действующих сил зависит также от ее суммарной массы и распределения масс. Масса системы (обозначаем М или) равна арифметической сумме масс всех точек или тел, образующих систему.
распределение масс в системе определяется значениями масс ее точек и их взаимными положениями, т. е. их координатами Однако оказывается, что при решении тех задач динамики, которые мы будем рассматривать, в частности динамики твердого тела, для учета распределения масс достаточно знать не все величины, а некоторые, выражаемые через них суммарные характеристики. Ими являются: координаты центра масс(выражаются через суммы произведений масс точек системы на их координаты), осевые моменты инерции(выражаются через суммы произведений масс точек системы на квадраты их координат) и центробежные моменты инерции (выражаются через суммы произведений масс точек системы и двух из их координат). Эти характеристики мы в данной главе и рассмотрим. Вопрос 11.2 Способы определения центра масс
Центр масс. В однородном поле тяжести, для которого g=const, вес любой частицы тела пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы (59) из § 32, определяющие координаты центра тяжести тела, к виду, явно содержащему массу. Для этого положим в названных формулах, после чего, сократив на g, найдем:
В полученные равенства входят теперь массы материальных точек (частиц), образующих тело, и координаты этих точек. Следовательно, положение точки действительно характеризует распределение масс в теле или в любой механической системе, если под понимать соответственно массы и координаты точек системы. Геометрическая точка С, координаты которой определяются формулами (1), называется центром масс илицентром инерции механической системы. Если положение центра масс определять его радиусом-вектором то из равенств (1) для получается формула
где — радиусы-векторы точек, образующих систему. Из полученных результатов следует, что для твердого тела, находящегося в однородном поле тяжести, положения центра масс и центра тяжести совпадают. Но в отличие от центра тяжести понятие о центре масс сохраняет свой смысл для тела, находящегося в любом силовом поле (например, в центральном поле тяготения), и, кроме того, как характеристика распределения масс, имеет смысл не только для твердого тела, но и для любой механической системы.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.207 (0.013 с.) |


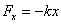


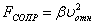
 позволяет определить, как меняется скорость тела
позволяет определить, как меняется скорость тела  по модулю и направлению, если на него в течение времени
по модулю и направлению, если на него в течение времени  действует сила
действует сила  .
. на него действует сила
на него действует сила  отлична от нуля. Именно эта проекция определяет действие силы, изменяющей скорость тела по модулю. Она совершает работу. Поэтому работу можно рассматривать как произведение проекции
отлична от нуля. Именно эта проекция определяет действие силы, изменяющей скорость тела по модулю. Она совершает работу. Поэтому работу можно рассматривать как произведение проекции  (рис.6.1):
(рис.6.1):

 , то
, то  . Следовательно, работа равна:
. Следовательно, работа равна:
 , то
, то  , так как косинус острых углов положителен. При
, так как косинус острых углов положителен. При  работа отрицательна, так как косинус тупых углов отрицателен. При
работа отрицательна, так как косинус тупых углов отрицателен. При 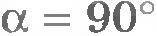 (сила перпендикулярна перемещению) работа не совершается. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. При движении спутника по круговой орбите сила тяготения также не совершает работу.
(сила перпендикулярна перемещению) работа не совершается. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. При движении спутника по круговой орбите сила тяготения также не совершает работу.


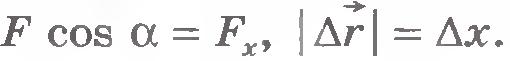

 , то и работа будет равна единице. В Международной системе единиц (СИ) работа измеряется в джоулях (обозначается Дж):
, то и работа будет равна единице. В Международной системе единиц (СИ) работа измеряется в джоулях (обозначается Дж):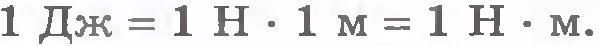
 .
.