
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие колебания. Дифференциальное уравнение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ри выводе уравнения гармонических колебаний считалось, что колеблющаяся точка находится под действием только квазиупругой силы. Во всякой реальной колебательной системе всегда имеются силы сопротивления (например, это может быть сила трения в точке подвеса, сопротивление среды, в которой совершаются колебания). Действие этих сил приводит к тому, что энергия колеблющейся системы (или точки) будет непрерывно убывать. Эта убыль энергии будет равна работе против сил трения и сопротивления. Т.к. полная энергия колебаний пропорциональна квадрату амплитуды Итак, затухание колебаний в любой колебательной системе (механической, электрической и т.п.) обусловлено потерями энергии в этой системе. Потери энергии колебаний в механических колебательных системах происходят из-за трения (внешнего и внутреннего) и излучения упругих волн в окружающую среду; в электрических – из-за наличия активного сопротивления проводников и т.п. Рассмотрим свободные (или собственные) колебания. Это значит, что система, будучи выведена из положения равновесия в результате внешнего воздействия, в дальнейшем предоставлена самой себе и находится под воздействием только квазиупругой силы F=-kx и силы сопротивления среды, значит она будет совершать затухающие колебания вдоль оси “x”. Ограничимся рассмотрением малых колебаний, тогда и скорость (v) системы будет малой, а при небольших скоростях сила сопротивления пропорциональна скорости:
где r – коэффициент сопротивления среды. Знак минус (“-”), т.к. Под действием сил F и f тело приобретает ускорение “a”, и для колеблющегося тела уравнение II-закона Ньютона имеет вид:
Обозначим
Здесь w0 – та частота, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды (т.е. при r = 0). Эта частота называется собственной частотой колебаний системы. b – коэффициент затухания колебаний (зависит от свойств данной системы и среды). Наличие сопротивления среды приводит к тому, что амплитуда колебаний со временем будет уменьшаться. Поэтому будем искать решение уравнения (8.15) в виде:
где a(t) – некоторая функция времени. Продифференцируем это выражение по времени и найдем
После подстановки этих выражений в уравнение (8.15) и несложных преобразований придем к следующему соотношению:
Для того чтобы уравнение удовлетворялось при любых значения “t”, необходимо равенство нулю коэффициентов при “ sin ” и ” cos ”. Т.е. приходим к двум следующим уравнениям:
Первое уравнение представим в виде:
После интегрирования получим
Отсюда При w0 > b, величина w будет вещественной и тогда решение дифференциального уравнения
Таким образом, при не слишком большом затухании
График этой функции показан на рисунке 8.9. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Движение такой системы можно рассматривать как гармоническое колебание с частотой w и амплитудой, изменяющееся по закону Скорость затухания колебаний определяется величиной Следовательно, коэффициент затухания равен обратной величине того промежутка времени, за который амплитуда колебаний уменьшается в “e” раз. С учетом того, что
При незначительном сопротивлении среды Для характеристики колебательной системы (а именно: убывания амплитуды колебаний в зависимости от числа колебаний) вводится величина, называемая логарифмическим декрементом затухания (l). Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период равно
Следовательно, логарифмический декремент затухания равен обратной Для характеристики колебательной системы также часто употребляется величина Как известно, энергия колеблющейся системы пропорциональна квадрату амплитуды. Поэтому энергия системы при затухающих колебаниях убывает со временем по закону
где E 0 – значение энергии при t = 0. Продифференцировав это выражение по “t”, получим скорость возрастания энергии
Изменив знак на обратный, найдем скорость убывания энергии: Если энергия мало изменяется за время равное периоду колебаний, то убыль энергии за период будет равна С учетом Из формулы для периода колебаний И последнее, математический анализ показывает, что при условии Вопрос 26.1 Вывод затухающих колебаний Затухающие колебания В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой Fy в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: Fтр =
Разделив левую и правую части уравнения (8) на m, обозначив r/m = 2b и сохранив обозначение к/m = w02 , приведем это уравнение к виду:
Решение этого уравнения имеет вид:
Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы b и w. Коэффициент b = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний w. Это уменьшение зависит от коэффициента затухания. Оказывается, что
Колебательный процесс может происходить лишь при условии: (w02 - b 2)>0, когда частота w в формуле (11) является действительной величиной. Если же затухание в системе слишком велико (w0 < b), то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера. Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 886; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.007 с.) |

 , то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих).
, то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих). ,
, и
и  имеют противоположные направления.
имеют противоположные направления. или
или  .
. ;
;  , тогда
, тогда

 и
и 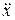 :
:

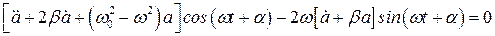 .
.

 или
или  .
. , где
, где  – постоянная интегрирования. После потенцирования найденного выражения получим
– постоянная интегрирования. После потенцирования найденного выражения получим  . Видно, что
. Видно, что  , а
, а  . Подставим эти значения в (8.17), получим
. Подставим эти значения в (8.17), получим .
. .
. может быть представлено в виде
может быть представлено в виде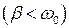 колебания описываются функцией
колебания описываются функцией
 .
. Верхняя из пунктирных кривых дает график функции a(t), причем величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы a:
Верхняя из пунктирных кривых дает график функции a(t), причем величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы a:  .
. , которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению
, которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению  .
. , а
, а  период затухающих колебаний можно определить как
период затухающих колебаний можно определить как .
. период колебаний практически равен
период колебаний практически равен  . С ростом коэффициента затухания период колебаний увеличивается.
. С ростом коэффициента затухания период колебаний увеличивается.
 , т.е.
, т.е.  . Т.к.
. Т.к.  . Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды.
. Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды. Выразим
Выразим  и запишем закон убывания амплитуды в виде
и запишем закон убывания амплитуды в виде 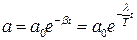 . За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит
. За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит  колебаний. Из условия
колебаний. Из условия  получаем
получаем  . Поэтому
. Поэтому  .
. величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина).
величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина). , называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз.
, называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз. ,
,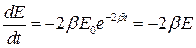 .
. .
.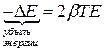 .
.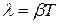 и
и  , т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.
, т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний. движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний. . Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:
. Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению: 8)
8) (9)
(9) (10)
(10) (11)
(11)


