
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импульс. Теорема об изменении импульса. Зси.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И́мпульс (коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
И́мпульс (Коли́честводвиже́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
Импульс системы частиц есть векторная сумма импульсов ее отдельных частиц: p=(сумм) pi, где pi – импульс i-й частицы. Теорема об изменении импульса системы: полный импульс системы можно изменить только действием внешних сил: Fвнеш=dp/dt(1), т.е. производная импульса системы по времени равна векторной сумме всехвнешних сил, действующих на частицы системы. Как и в случае одной частицы, из выражения (1) следует, что приращение импульса системы равно импульсу результирующей всех внешних сил за соответствующий промежуток времени: p2-p1=t&0Fвнешнdt. В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:
соответственно величина Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками и просуммировать по ним, в результате получим:
Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:
Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*). В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина
где mi — масса i -й материальной точки. Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта. Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как
На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:
В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения. Свойства импульса · Аддитивность. Это свойство означает, что импульс механической системы, состоящей из материальных точек, равен сумме импульсов всех материальных точек, входящих в систему.[2] · Инвариантность по отношению к повороту системы отсчета. [2] · Сохранение. Импульс не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея[2] Свойства сохранения кинетической энергии, сохранения импульса и второго закона Ньютона достаточно, чтобы вывести математичекую формулу импульса.[3][4]
Зако́нсохране́нияи́мпульса (Зако́нсохране́ния количества движения) - векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной изфундаментальных симметрий, — однородностью пространства Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона
Тогда отношение изменения импульса системы к изменению времени равняется сумме всех внешних сил. Это и есть одна из формулировок закона изменения импульса. Классическая формулировка гласит: Изменение импульса
3) Из второго закона Ньютона
Вопрос 14 Момент импульса. Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1]. Момент импульса материальной точки относительно точки O определяется векторным произведением Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени. Аналогично для замкнутой системы тел, вращающихся вокруг оси z:
Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Вопрос 14.1
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 4038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |




 называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).
называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).
 . (*)
. (*) ,
,

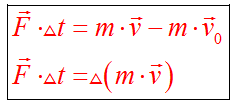

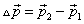 тела изображено на рисунке
тела изображено на рисунке

 , где
, где  — радиус-вектор, проведенный из точки O,
— радиус-вектор, проведенный из точки O,  — импульс материальной точки.
— импульс материальной точки. равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса
равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса  , получим
, получим .
. .
. .
. отсюда
отсюда  или
или  .
.


