
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент инерции некоторых однородных тел.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Момент инерции J (кгм2) – параметр, аналогичный по физическому смыслу массе при поступательном движении. Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения: Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. Он может быть выражен через массу тела и его размеры[1]. Моменты инерции однородных тел простых форм приведены в табл. 2.1.
Таблица 2.1 Моменты инерции некоторых однородных тел
Момент инерции тела, если известно распределение массы тела относительно оси вращения mi (R), может быть определён как
Детали электропривода, например ротор электрической машины, представляют собой конструкции, состоящие из деталей сложных форм и изготовленные из материалов различной плотности. Следовательно, расчёт момента инерции связан со значительными трудностями. В случаях, когда расчёт момента инерции не возможен либо затруднён, используют следующие методы экспериментального определения момента инерции. Метод свободного выбега (самоторможения) [2]. Сущность этого метода состоит в следующем. Исследуемый агрегат, включающий в себя электродвигатель и механически соединённые с ним элементы, разгоняется до некоторой установившейся частоты вращения в режиме х.х.
С другой стороны, эта энергия может быть определена как произведение мощности, затраченной на приведение во вращение агрегата в режиме х.х.
Приравняв (9.1) к (9.2), получим выражение общего момента инерции, кг·м2:
Значения Метод вспомогательного маятника. Этот метод применяют в тех случаях, когда метод свободного выбега не может быть использован, в частности для электрических машин большой мощности – до 1000 кВт. Для реализации этого метода вращающуюся часть машины устанавливают на подшипниках балансировочного станка. Если вращающаяся часть машины имеет собственные подшипники, то могут быть использованы и они. Испытания проводят на собственной машине. У коллекторных машин или асинхронных двигателей с фазным ротором при определении момента инерции следует поднять щётки. При использовании метода вспомогательного маятника к валу исследуемой вращающейся части прикрепляют дополнительную массу mдоп центр тяжести которой находится на расстоянии а от центра вала. Вращающуюся часть вместе со вспомогательным маятником следует привести в колебательное движение. При этом одностороннее угловое отклонение не должно превышать 15о. Период колебаний принимают как средний из нескольких колебаний. Для точности рекомендуется производить измерения периода колебаний в момент нахождения маятника через положение статического равновесия. Момент инерции испытуемой вращающейся части определяется по формуле Для повышения точности измерения момента инерции рекомендуется проводить измерения несколько раз с разными значениями дополнительной массы вспомогательного маятника mдоп или расстояния а. [3] Вопрос 12.2 Момент инерции относительно параллельных осей(формула Гюйгенса)
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.126.33 (0.007 с.) |

 .
.


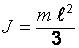




 . (2.11)
. (2.11) . После этого электродвигатель отключают от сети и наступает процесс самопроизвольного торможения, т.е. торможения исключительно за счёт внутренних сил трения в подшипниках электродвигателя и сочленённых с ним вращающих частей о воздух. На преодоление этих сил трения затрачивается кинетическая энергия (Дж), запасенная во вращающихся частях агрегата:
. После этого электродвигатель отключают от сети и наступает процесс самопроизвольного торможения, т.е. торможения исключительно за счёт внутренних сил трения в подшипниках электродвигателя и сочленённых с ним вращающих частей о воздух. На преодоление этих сил трения затрачивается кинетическая энергия (Дж), запасенная во вращающихся частях агрегата: . (2.12)
. (2.12) на время
на время 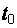 :
: . (2.13)
. (2.13) . (2.14)
. (2.14)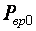 и
и  .
. . (2.15)
. (2.15)


