
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о ламинарном и турбулентном потоках. Число Рейнольдса.Содержание книги
Поиск на нашем сайте
Наблюдается два вида течения жидкости (или газа). В одних случаях жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь. Такое течение называется ламинарным (слоистым). Если в ламинарный поток ввести подкрашенную струйку, то она сохраняется, не размываясь, на всей длине потока, так как частицы жидкости в ламинарном потоке не переходят из одного слоя в другой.Ламинарное течение стационарно. При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется. Возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. При турбулентном течении скорость частиц в каждом данном месте все время изменяется беспорядочным образом — течение нестационарно. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места ее введения окрашенная жидкость равномерно распределяется по всему сечению потока. Английский ученый Рейнольдс установил, что характер течения зависит от значения безразмерной величины:
где Величина (76.1) называется числом Рейнольдса. При малых значениях числа Рейнольдса наблюдаетсяламинарное течение. Начиная с некоторого определенного значения Отношение Кинематическая и динамическая вязкость
называется кинематической вязкостью. В отличие от v величина
Число Рейнольдса может служить критерием подобия для течения жидкостей в трубах, каналах и т. д. Характер течения различных жидкостей (или газов) в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение Re. Вопрос 40 Специальная теория относительности Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.
Вопрос 40.1 Принцип относительности Галилея. Преобразование координат Галилея. ринцип относительности Галилея гласит: Механические явления протекают одинаково во всех инерциальных системах отсчета, т. е. описывающие их законы динамикиодинаковы. Поэтому все инерциальные системы отсчета равноправны. Это значит, что уравнения, выражающие законы механики, не меняются при преобразованиях Галилея. Преобразования Галилея заключаются в преобразовании координат
Для координаты x это выражается так:
Здесь
В некоторый начальный момент времени t0 = 0 возьмем одну из систем координат К (XYZ) и совместим с подвижной – K ´(X ´ Y ´ Z ´). Зафиксируем систему K. В любой последующий момент времени положение некоторой точки А, движущейся относительно обеих систем координат, определяется в системе K радиус-вектором
Из этого уравнения вытекает закон сложения скоростей:
где Галилей на основании наблюдений сформулировал классический принцип относительности, согласно которому законы механики одинаковы в любых инерциальных системах отсчета. То есть, уравнения движения относительно любых инерциальных систем совпадают друг с другом. Это значит, что уравнение mw =F эквивалентно уравнению m´w´ = F´. Из принципа Галилея следует, что F=F´, т. е. силы, действующие на точку, неизменны при переходе от одной инерциальной системы к другой, также инерциальной системе. Следовательно, все величины, входящие в уравнение Ньютона, не изменяются при преобразовании от одной инерциальной системы к другой инерциальной системе. Вопрос 41
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.149 (0.005 с.) |


 — плотность жидкости (или газа), v — средняя (по сечению трубы) скорость потока,
— плотность жидкости (или газа), v — средняя (по сечению трубы) скорость потока,  — коэффициент вязкости жидкости, l — характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении и т. д.
— коэффициент вязкости жидкости, l — характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении и т. д.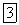 называемого критическим, течение приобретает турбулентный характер. Если в качестве характерного размера для круглой трубы взять ее радиус
называемого критическим, течение приобретает турбулентный характер. Если в качестве характерного размера для круглой трубы взять ее радиус  , то критическое значение числа Рейнольдса (которое в этом случае имеет вид
, то критическое значение числа Рейнольдса (которое в этом случае имеет вид  ) оказывается равным примерно 1000. В число Рейнольдса входят в виде отношения две величины, зависящие от свойств жидкости: плотность
) оказывается равным примерно 1000. В число Рейнольдса входят в виде отношения две величины, зависящие от свойств жидкости: плотность  и коэффициент вязкости
и коэффициент вязкости 
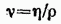
 называется динамической вязкостью. Используя кинематическую вязкость, числу Рейнольдса можно придать следующий вид;
называется динамической вязкостью. Используя кинематическую вязкость, числу Рейнольдса можно придать следующий вид;
 и времени t движущейся материальной точки при переходе от одной инерциальной системы отсчета к другой:
и времени t движущейся материальной точки при переходе от одной инерциальной системы отсчета к другой:

 и
и  - радиус-векторы,
- радиус-векторы,  и
и  - координаты точки в двух инерциальных системах отсчета, а υ – относительная скорость движения этих двух инерциальных систем отсчета. Время не изменяется при переходе из одной инерциальной системы отсчета в другую: принцип относительности Галилея основан на представлениях об абсолютном времени и абсолютном пространстве. Это означает, что во всех инерциальных системах отсчета события протекают одинаково (одновременно).
- координаты точки в двух инерциальных системах отсчета, а υ – относительная скорость движения этих двух инерциальных систем отсчета. Время не изменяется при переходе из одной инерциальной системы отсчета в другую: принцип относительности Галилея основан на представлениях об абсолютном времени и абсолютном пространстве. Это означает, что во всех инерциальных системах отсчета события протекают одинаково (одновременно).
 . Согласно правилу сложения векторов,
. Согласно правилу сложения векторов,  . Выразив вектор перемещения через скорость движения системы K ´ относительно K, получим
. Выразив вектор перемещения через скорость движения системы K ´ относительно K, получим  . Исходя из этого,
. Исходя из этого,
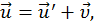
 - скорости точки относительно систем K и K´ соответственно. Дифференцируем по времени это выражение и получим w = w ´. Это значит, что ускорение точки в данный момент времени одинаково относительно любой из систем, неускоренно движущихся относительно друг друга.
- скорости точки относительно систем K и K´ соответственно. Дифференцируем по времени это выражение и получим w = w ´. Это значит, что ускорение точки в данный момент времени одинаково относительно любой из систем, неускоренно движущихся относительно друг друга.


