
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула атмосферного давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос 35 Стационарное течение жидкости Стационарное течение жидкости. Уравнение неразрывности Рассмотрим случай, когда невязкая жидкость течет по горизонтальной цилиндрической трубе с изменяющимся поперечным сечением.
Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется. При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости. Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы. Пусть скорости стационарного течения жидкости через сечения трубы S1 и S2 равны соответственно v1 и v2. Объем жидкости, протекающей за промежуток времени t через сечение S1, равен V1=S1v1t, а объем жидкости, протекающей за то же время через сечение S2, равен V2=S2v2t. Из равенства V1=V2 следует, что S1v1=S2v2. (1) Соотношение (1) называют уравнением неразрывности. Из него следует, что v1/v2=S2/S1. Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений. Давление в движущейся жидкости. Закон Бернулли Увеличение скорости течения жидкости при переходе из участка трубы с большей площадью поперечного сечения в участок трубы с меньшей площадью поперечного сечения означает, что жидкость движется с ускорением. Согласно второму закону Ньютона, причиной ускорения является сила. Этой силой в данном случае является разность сил давления, действующих на текущую жидкость в широкой и узкой частях трубы. Следовательно, в широкой части трубы давление жидкости должно быть больше, чем в узкой. Это можно непосредственно наблюдать на опыте. На рис. показано, что на участках разного поперечного сечения S1 и S2 в трубу, по которой течет жидкость, вставлены манометрические трубки. Как показывают наблюдения, уровень жидкости в манометрической трубке у сечения S1 трубы выше, чем у сечения S2. Следовательно, давление в жидкости, протекающей через сечение с большей площадью S1, выше, чем давление в жидкости, протекающей через сечение с меньшей площадью S2. Следовательно, при стационарном течении жидкости в тех местах, где скорость течения меньше, давление в жидкости больше и, наоборот, там, где скорость течения больше, давление в жидкости меньше. К этому выводу впервые пришел Бернулли, поэтому данный закон называется законом Бернулли. Вопрос 36.37 Уравнение Бернулли вывод Выделим в стационарно текущей идеальной жидкости (физическая модель - воображаемая жидкость, в которой нет сил внутреннего трения) трубку тока, которая ограничена сечениями S 1 и S 2, (рис. 1). Пусть в месте сечения S 1 скорость течения ν 1, давление p1 и высота, на которой это сечение расположено, h 1. Аналогично, в месте сечения S 2 скорость течения ν 2, давление p2 и высота сечения h 2.
Рис.1
За бесконечно малый отрезок времени Δt жидкость двигается от сечения S 1 к сечению S 1', от S 2 к S 1'. По закону сохранения энергии, изменение полной энергии E2-E1 идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:
где E1 и E2 - полные энергии жидкости массой m в местах сечений S 1 и S 2 соответственно. С другой стороны, А - это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S 1 и S 2, за рассматриваемый малый отрезок времени Δt. Чтобы перенести массу m от S 1 до S 1' жидкость должна переместиться на расстояние l 1= ν 1Δt и от S 2 до S 1' - на расстояние l 2= ν 2Δt. Отметим, что l 1 и l 2 настолько малы, что всем точкам объемов, закрашенных на рис. 1, приписывают постоянные значения скорости ν, давления р и высоты h. Следовательно,
где F1 = p1 S 1 и F2 = - p2 S 2 (отрицательна, так как направлена в сторону, противоположную течению жидкости; рис. 1). Полные энергии E1 и E2 будут складываться из кинетической и потенциальной энергий массы m жидкости:
Подставляя (3) и (4) в (1) и приравнивая (1) и (2), получим
Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.
Разделив выражение (30.5) на ΔV, получим
где ρ - плотность жидкости. Поскольку сечения выбирались произвольно, то
Выражение (6) получено швейцарским физиком Д. Бернулли (1700-1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Из его вывода видно, что уравнение Бернулли - форма закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико. Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина ρν2/2 - динамическим давлением, величина ρgh - гидростатическое давление. Для горизонтальной трубки тока (h 1= h 2) выражение (6) будет вид
где p+ρν2/2 называется полным давлением. Из уравнения Бернулли (7) для горизонтальной трубки тока и уравнения неразрывности видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах, а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров (рис. 2).
Рис.2
Данный опыт показывает, что в манометрической трубке В, которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, которые прикрепленны к широкой части трубы, что соответствует уравнению Бернулли. Так как динамическое давление зависит от скорости движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито - Прандтля (рис. 3), состоящая из двух изогнутых под прямым углом трубок, с присоединенными к манометру противоположными концами.
Рис.3
С помощью одной из трубок измеряется полное давление (р0), с помощью другой - статическое (р). С помощью манометра измеряют разность давлений:
где ρ0 - плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:
Из формул (8) и (9) получаем искомую скорость потока жидкости:
Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис. 4). Струя воды подается в трубку, которая открыта в атмосферу, значит давление на выходе из трубки равно атмосферному. В трубке сделано сужение, по которому вода течет с большей скоростью. В данном месте давление меньше атмосферного. Такое же давление деалется и в откачанном сосуде, связанным с трубкой через разрыв, сделанный в ее узкой части. Воздух переносится вытекающей с большой скоростью водой из узкого конца. Таким способом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. =133,32 Па).
Рис.4
Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью,с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости (рис. 5).
Рис.5
Рассмотрим два сечения (на уровне h 1 свободной поверхности жидкости в сосуде и на уровне h 1 выхода ее из отверстия) и применим уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р1=р2, то уравнение будет иметь вид
Из уравнения неразрывности мы знаем, что ν 2/ ν 2= S 1/ S 2, где S 1 и S 2 - площади поперечных сечений сосуда и отверстия. Если S 1>> S 2, то слагаемым ν 12/2 можно пренебречь и
Это выражение получило название формулы Торричелли Вопрос 38 Вязкость. Вязкость – это свойство жидкости оказывать сопротивление сдвигающим усилиям. Вязкость - свойство, присущее как капельным жидкостям, так и газам, которое проявляется только при движении, не может быть обнаружено при покое, и проявляется в виде внутреннего трения при перемещении смежных частиц жидкости. Вязкость характеризует степень текучести жидкости и подвижности ее частиц. Вязкостью жидкостей объясняется сопротивление и потери напор, которое возникает при движении их по трубам, каналам и прочим руслам, а также при движении в них инородных тел. Вопрос 38.1
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |




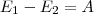 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)
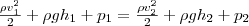
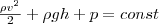 (6)
(6) (7)
(7)

 (8)
(8) (9)
(9)







