
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимосвязь между омегой и скоростью при равномерном вращении твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вращательное движение вокруг неподвижной оси - еще один частный случай движения твердого тела.
В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов.
Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол
Угловая скорость выражается в радианах в секунду (рад/с).
Полному обороту тела соответствует угол
Если при равномерном вращении угловая скорость известна и в начальный момент времени
Если
Так как
Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора
Следовательно,
Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Вопрос 9 Законы динамки.
Раздел механики, изучающий движение тела под воздействием приложенных к нему сил, называется динамика. А классической называется динамика, которая базируется на законах Ньютона. Им в 1687 году были сформулированы основные законы динамики. Именно о них и пойдет речь в нашей статье. Закон инерции Это первый закон динамики, описывающий самое простое механическое движение материальной точки в условиях полной изолированности ее от воздействия других материальных объектов. В этом законе говорится о том, что любая изолированная материальная точка, то есть такая точка, которая не подвержена влиянию других материальных тел, может совершать по отношению к какой–либо неподвижной системе отсчета только равномерное прямолинейное движение (скорость в данном случае величина постоянная) или находиться в состоянии покоя (скорость равна нулю). Свойство материальной точки сохранять неизменным состояние движения, при отсутствии сил, которые на нее действуют, или они равновесны, называется инерцией этой точки. Инерциальной или основной называется система отсчета, в отношении которой закон инерции справедлив. А абсолютным движением называется движение относительно этой системы. Инерциальной является также любая другая система отсчета, которая движется по отношению к данной инерциальной системе прямолинейно, поступательно, равномерно. Систему, которая неподвижно связана с Землей, также принимают за инерциальную систему. Правда делается это с приближением, которого достаточно для практических решений. Второй закон Продолжая изучать законы динамики, рассмотрим второй закон, который так и называется основной закон динамики. Нарушение инерционного состояния материальной точки, то есть появление ее ускорения, возникает под воздействием на нее других материальных объектов или точек. Характеризует это воздействие векторная величина, называемая силой, приложенной к этой точке. Характеристики силы: Направление воздействия на материальную точку со стороны другого тела или точки. Интенсивность воздействия на точку и зависимость ее ускорения от сопротивляемости данному воздействию. Способность материальной точки сопротивляться изменению равномерного прямолинейного движения или состояния покоя представляет собой инертность. Ее мерой является масса, m. Второй основной закон динамики говорит о том, что сила, которая действует на материальную точку, является величиной пропорциональной массе этой точки и ускорению, которое сообщается точке приложенной к ней силой. F = kmw, где F-вектор приложенной силы, m-масса тела, w-вектор ускорения и k-коэффициент пропорциональности. Если коэффициент пропорциональности принять за 1, то основной закон динамики будет выражаться так: F=mw, где w является абсолютным ускорением тела, то есть ускорением по отношению к некой инерциальной СО. Из этого следует, что мы можем определить массу точки, исходя из того ускорения, которое было получено ею при воздействии известной силы. Ускорение свободного падения вблизи Земли является величиной постоянной. Сила, которая сообщает телу данное ускорение, называется весом. Отсюда будет вытекать понятие весомой массы. Третий закон Закон равенства противодействия и действия является также аксиомой статики. Говорит этот закон о том, что силы взаимодействия двух материальных точек действуют по направлению одной прямой. Направлены они противоположно и численно между собой равны, то есть F12 = F21. Если силы представить, как F12 = m1w1 и F21 = m2w2, то поскольку F12 = F21, то получаем, что m1w1 = m2w2, отсюда следует, что w1/w2 = m1/m2. Означает это, что ускорения, вернее их модули, сообщаемые друг другу материальными телами при их взаимодействии, будут обратно пропорциональны массам этих тел. Четвертый закон Мы рассмотрели еще не все законы динамики. Рассмотрим четвертый закон, закон независимости действия сил. Он говорит о том, что материальное тело под воздействием нескольких сил получит ускорение, которое будет равно геометрической сумме ускорений, которые оно получит от каждой силы. Силы эти действуют отдельно и независимо друг от друга. Таким образом, система сил, которые были приложены к одному материальному телу, будет эквивалентна одной равнодействующей силе, которая равна главному вектору всей системы сил. Обязательно следует обратить внимание на то, что основные законы динамики Ньютона можно рассматривать только лишь в тесной взаимосвязи друг с другом. В этом случае они являются фундаментом динамики – науки, описывающей механическое движение, выясняющей причины изменения скоростей объектов, объясняющей и управляющей этим движением.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |


 разные пути. Так,
разные пути. Так,  , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время
, поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время  . Угол
. Угол  - угол между осью ОХ и радиус-вектором
- угол между осью ОХ и радиус-вектором  , определяющим положение точки А (см. рис.2.5).
, определяющим положение точки А (см. рис.2.5).
 , а другое - на угол
, а другое - на угол  , то мы говорим, что первое тело вращается быстрее второго в 2 раза.
, то мы говорим, что первое тело вращается быстрее второго в 2 раза.
 (греческая буква «ню») оборотов за 1с, то время одного оборота равно
(греческая буква «ню») оборотов за 1с, то время одного оборота равно  секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:
секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:
 . Поэтому согласно формуле (2.1)
. Поэтому согласно формуле (2.1)
 угол поворота
угол поворота  , то угол поворота тела за время t согласно уравнению (2.1) равен:
, то угол поворота тела за время t согласно уравнению (2.1) равен: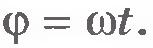
 , то
, то  , или
, или  .
. . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
. Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
 , то
, то
 , а для точек на широте Санкт-Петербурга
, а для точек на широте Санкт-Петербурга  . На полюсах Земли
. На полюсах Земли  .
.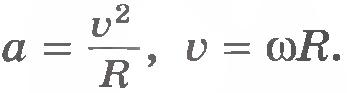

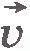 и
и  , a также форму траекторий точек.
, a также форму траекторий точек.



