
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований? Ответ 1320Стр 1 из 9Следующая ⇒
Векторы. Основные понятия. Линейные операции над векторами.?.Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований? Под вектором в элементарной математике понимают направленный отрезок. Этот отрезок изображается стрелкой и обозначается или одной буквой со стрелкой (
Рис.1. Векторы
либо, как мы условимся в настоящем издании, жирным шрифтом Модулем (абсолютной величиной) вектора называется длина отрезка, изображающего этот вектор. Модуль обозначается Коллинеарными называются два ненулевых вектора, лежащих на одной прямой, либо на параллельных прямых. Коллинеарные векторы Два или более векторов называются компланарными, если они лежат в одной плоскости. Очевидно, что два коллинеарных вектора всегда компланарны. Будем считать, что вектор не зависит от того, где находится начало (такие вектора называются свободными). Два свободных вектора называются равным и, если они параллельны и имеют равные модули: Пусть имеется два ненулевых вектора
Рис.1.2 Сложение векторов Можно также использовать следующее из правила треугольника правило параллелограмма: суммой двух неколлинеарных векторов
Рис.3. Сложение векторов
Вектор, антипараллельный данному вектору
Рис.4. Разность векторов Произведением вектора Из приведенных выше правил сложения векторов и умножения их на число следуют очевидные утверждения: 1. 2. 3. 4. 5. 6. 7. 8. В линейной алгебре множество элементов произвольной природы, на котором определены операции сложения и умножения на число, а также справедливы утверждения (1-8), называют линейным пространством, а сами элементы - векторами (в широком смысле) этого пространства. Таким образом, введенные векторы, как направленные отрезки, образуют линейное пространство.
В физике часто приходится иметь дело с такими свойствами, для определения которых, кроме их численного значения, необходимо указывать и направление в пространстве. Например, скорость, ускорение, сила, момент силы, напряженность электрического или магнитного поля и т. п. Из физического определения этих величин следует, что они являются векторами в своем линейном пространстве - для них выполняются (1-8). Эти физические величины имеют такую же "внутреннюю структуру", что и направленные отрезки. Поэтому логически непротиворечивые правила работы с такими физическими характеристиками можно изучать на примере "работы" с математическими векторами из линейного пространства. Подчеркнем, что свойства (1-8) являются определяющими для вектора. Например, поворот твердого тела на конечный угол вокруг некоторой оси можно задавать с помощью направленного отрезка
Вариационный ряд. Последовательность значений вариант, расположенных в возрастающем порядке, называется вариационным рядом.Статистическим распределением называют вариационный ряд значений выборки и соответствующих им частот ni или относительных частот Wi.
Полигон и гистограмма. Полигоном частот (относительных частот) называется ломаная линия с вершинами в точках (xk , nk), где xk – варианта, nk – ее частота, или (xk , Wk), где Wk - относительная частота.Для непрерывных распределений более наглядное представление о характере распределения случайной величины дает гистограмма. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотой ni/h, где h - длина каждого частичного интервала.Если соединить середины верхних прямоугольников гистограммы, то получим полигон частот. Исправленная дисперсия
10. Среднее квадратическое отклонение равно квадратному корню из дисперсии:
Среднее квадратическое отклонение называют также стандартным отклонением. 11. Коэффициент вариации V - это выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
Общие сведения о дифференциальных уравнениях. Основные понятия. Задача Коши Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него. Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
где Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
где
Различные постановки задачи Коши
Числовые ряды. Основные понятия. Необходимый признак сходимости числового ряда Пусть положительные числа называется числовым рядом. Здесь Зная общий член ряда, можно записать ряд в форме (1). Так общим членом Рассмотрим для числового ряда (1) суммы его первых членов Будем называть их частичными суммами и обозначим соответственно через Если для некоторого числового ряда бесконечная последовательность его частичных сумм имеет конечный предел, то этот ряд называется сходящимся. Этот предел Если последовательность частичных сумм ряда не имеет определенного предела, то ряд называется расходящимся и для него не существует суммы. Рассмотрим примеры на исследование сходимости ряда по определению. Пример 1. Дан ряд Это геометрическая прогрессия с первым членом Частичная сумма ряда 1) если Значит, в случае 2) если 3) если В этом случае 4) если В этом случае Следовательно, Таким образом, ряд
Пример 2. Рассмотрим ряд который называется обобщенным гармоническим рядом. 1) пусть Составим n-ю частичную сумму По условию 2) при т.о. обобщенный гармонический ряд При Пример 3. Рассмотрим ряд Общий член заданного ряда может быть представлен в виде: Определим частичную сумму ряда Отсюда Для рассмотренных рядов операция суммирования оказалась сравнительно несложной. Вообще же этот прием, если он и выполним, связан со сложными вычислениями. Поэтому для исследования характера ряда применяют признаки сходимости. 2. Необходимый признак сходимости. Теорема. Если числовой ряд Доказательство. Пусть данный ряд сходится. Тогда по определению сходящегося ряда так как вместе с Здесь Поэтому Отсюда Элементы комбинаторики. Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой. Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать kспособами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами. Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7. Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций: Размещение без повторений. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из kэлементов (k£m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой
Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются? Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно: Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются? Решение. Количество чисел равно числу перестановок из четырех элементов: Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k £ m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний изm элементов по k элементов вычисляется по формуле: Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции? Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: Формула Бернулли Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна: Pn(k)=Cnkpkqn-k или
где q=1-p Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, — находят соответственно по формулам:
Pn(0)+Pn(1)+...+Pn(k-1); Pn(k+1)+Pn(k+2)+...+Pn(n); Pn(k)+Pn(k+1)+...+Pn(n); Pn(0)+Pn(1)+...+Pn(k);
Векторы. Основные понятия. Линейные операции над векторами.?.Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований? Под вектором в элементарной математике понимают направленный отрезок. Этот отрезок изображается стрелкой и обозначается или одной буквой со стрелкой (
Рис.1. Векторы
либо, как мы условимся в настоящем издании, жирным шрифтом Модулем (абсолютной величиной) вектора называется длина отрезка, изображающего этот вектор. Модуль обозначается Коллинеарными называются два ненулевых вектора, лежащих на одной прямой, либо на параллельных прямых. Коллинеарные векторы Два или более векторов называются компланарными, если они лежат в одной плоскости. Очевидно, что два коллинеарных вектора всегда компланарны. Будем считать, что вектор не зависит от того, где находится начало (такие вектора называются свободными). Два свободных вектора называются равным и, если они параллельны и имеют равные модули: Пусть имеется два ненулевых вектора
Рис.1.2 Сложение векторов Можно также использовать следующее из правила треугольника правило параллелограмма: суммой двух неколлинеарных векторов
Рис.3. Сложение векторов
Вектор, антипараллельный данному вектору
Рис.4. Разность векторов Произведением вектора Из приведенных выше правил сложения векторов и умножения их на число следуют очевидные утверждения: 1. 2. 3. 4. 5. 6. 7. 8. В линейной алгебре множество элементов произвольной природы, на котором определены операции сложения и умножения на число, а также справедливы утверждения (1-8), называют линейным пространством, а сами элементы - векторами (в широком смысле) этого пространства. Таким образом, введенные векторы, как направленные отрезки, образуют линейное пространство.
В физике часто приходится иметь дело с такими свойствами, для определения которых, кроме их численного значения, необходимо указывать и направление в пространстве. Например, скорость, ускорение, сила, момент силы, напряженность электрического или магнитного поля и т. п. Из физического определения этих величин следует, что они являются векторами в своем линейном пространстве - для них выполняются (1-8). Эти физические величины имеют такую же "внутреннюю структуру", что и направленные отрезки. Поэтому логически непротиворечивые правила работы с такими физическими характеристиками можно изучать на примере "работы" с математическими векторами из линейного пространства. Подчеркнем, что свойства (1-8) являются определяющими для вектора. Например, поворот твердого тела на конечный угол вокруг некоторой оси можно задавать с помощью направленного отрезка Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований? Ответ 1320
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1951; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.244.216 (0.139 с.) |
 ) (рис.1.1),
) (рис.1.1),
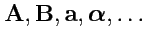 .
. . Модуль вектора является скаляром. Если начало и конец вектора совпадают, то вектор называется нулевым и обозначается как
. Модуль вектора является скаляром. Если начало и конец вектора совпадают, то вектор называется нулевым и обозначается как  . Если модуль вектора равен нулю, а направление не определено, то можно считать, что он направлен в любую сторону.
. Если модуль вектора равен нулю, а направление не определено, то можно считать, что он направлен в любую сторону. и
и  будем обозначать как
будем обозначать как  . Если неколлинеарные векторы направлены одинаково, их называют параллельными (сонаправленными) -
. Если неколлинеарные векторы направлены одинаково, их называют параллельными (сонаправленными) -  ; противоположно направленные коллинеарные векторы называют антипараллельными
; противоположно направленные коллинеарные векторы называют антипараллельными 
 .
.

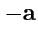 . Очевидно, что сумма противоположных векторов является нулевым вектором:
. Очевидно, что сумма противоположных векторов является нулевым вектором:  . Разностью
. Разностью 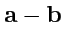 векторов
векторов  . Соединим начала векторов
. Соединим начала векторов  , тогда вектор
, тогда вектор 
 называется вектор
называется вектор 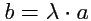 , причем
, причем  при
при  и
и  при
при  . Геометрически умножение
. Геометрически умножение  на число
на число  раз с сохранением направления при
раз с сохранением направления при  (сложение коммутативно);
(сложение коммутативно); (сложение ассоциативно);
(сложение ассоциативно); (существование нулевого вектора);
(существование нулевого вектора);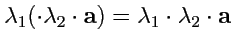 (сложение ассоциативно);
(сложение ассоциативно); (умножение на число дистрибутивно);
(умножение на число дистрибутивно); (сложение векторов дистрибутивно);
(сложение векторов дистрибутивно); .
. , параллельного оси вращения и по модулю равного углу поворота. Но такой "поворот" не будет вектором, так как повороты
, параллельного оси вращения и по модулю равного углу поворота. Но такой "поворот" не будет вектором, так как повороты  и
и  вокруг разных осей, вообще говоря, не коммутруют:
вокруг разных осей, вообще говоря, не коммутруют:  и, таким образом, свойство 1 из (1-8) не выполняется. В противоположность конечным поворотам, повороты на бесконечно малые углы являются векторами.
и, таким образом, свойство 1 из (1-8) не выполняется. В противоположность конечным поворотам, повороты на бесконечно малые углы являются векторами.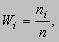
 .
. (8)
(8) (9)
(9) (10)
(10) не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных. до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет. или
или  ,
, — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной
— неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной  , штрих означает дифференцирование по
, штрих означает дифференцирование по  называется порядком дифференциального уравнения.
называется порядком дифференциального уравнения. ,
,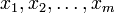 — независимые переменные, а
— независимые переменные, а 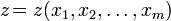 — функция этих переменных.
— функция этих переменных.
 ОДУ первого порядка, разрешённая относительно производных (нормальная система
ОДУ первого порядка, разрешённая относительно производных (нормальная система 

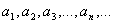 - члены некоторой бесконечной числовой последовательности. Тогда выражение вида
- члены некоторой бесконечной числовой последовательности. Тогда выражение вида (1)
(1)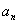 – общий член ряда, с помощью которого ряд (1) записывается в виде
– общий член ряда, с помощью которого ряд (1) записывается в виде
 задается числовой ряд
задается числовой ряд


 называется суммой ряда.
называется суммой ряда.
 и знаменателем
и знаменателем  .
. или
или  .
. , то
, то  , при
, при  и, следовательно,
и, следовательно,
 .
.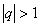 , то
, то  , при
, при  ,т.е.
,т.е.  не существует и ряд расходится
не существует и ряд расходится то данный ряд имеет вид
то данный ряд имеет вид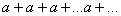
 , т.е. ряд расходится.
, т.е. ряд расходится. , то имеем ряд
, то имеем ряд

 предела не имеет и ряд расходится
предела не имеет и ряд расходится сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы.
сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы.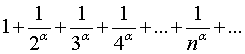 ,
,

 , т.о.
, т.о. , следовательно, ряд расходится
, следовательно, ряд расходится
 и ряд будет сходящимся.
и ряд будет сходящимся. расходится при
расходится при  получим ряд вида
получим ряд вида  , который называется гармоническим и является расходящимся рядом.
, который называется гармоническим и является расходящимся рядом.
 , сравнив числители дробей, получим значения
, сравнив числители дробей, получим значения  ,
,  и, таким образом,
и, таким образом, 

 , и, таким образом, заданный ряд сходится.
, и, таким образом, заданный ряд сходится.
 ;
; , то
, то  , т.е.
, т.е.
 , а
, а  .
.
 , что и требовалось доказать.
, что и требовалось доказать. .
.
 .
.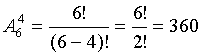



 .
.



