
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава III. Механика твердого телаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ГЛАВА III. МЕХАНИКА ТВЕРДОГО ТЕЛА Лабораторная работа № 5 ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ
ЦЕЛЬ РАБОТЫ Изучение характеристик вращательного движения твердого тела. Применение основного закона динамики вращательного движения для определения момента инерции тела.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z
аналогично второму закону Ньютона F = ma. В формуле (1) Мz - момент внешних сил, действующих на тело относительно оси z;
Модуль вектора
где h = r×sina - плечо силы, которое равно длине перпендикуляра, опущенного из точки О на направление силы. Вектор Момент силы относительно оси z равен проекции на эту ось момента силы относительно произвольной точки О, лежащей на оси z:
Момент силы Мz относительно оси - величина алгебраическая. Кроме формулы (4) для вычисления момента силы относительно оси z можно использовать формулу:
где Момент инерции тела Iz относительно оси z является мерой инертности тела при его вращении относительно этой оси и определяется формулой:
где Из формулы (6) видно, что момент инерции тела относительно оси равен сумме моментов инерции
Предел суммы (7) при
С помощью формулы (8) можно вычислять моменты инерции однородных тел правильной геометрической формы относительно осей, проходящих через центры масс этих тел. В частности, момент инерции однородного прямого круглого цилиндра массой m и радиусом основания R относительно оси z, проходящей через центр масс С этого цилиндра параллельно его боковой поверхности (рис.14 а), равен
Если же ось z перпендикулярна боковой поверхности такого цилиндра (рис.14 б), то момент инерции можно найти по формуле
где R - радиус основания, Н - высота цилиндра. Для вычисления момента инерции тела относительно произвольной оси z¢ применяется теорема Штейнера (рис.15): момент инерции тела I относительно произвольной оси z¢ равен сумме момента инерции Iс относительно оси z, параллельной данной оси z¢ и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
Момент инерции тела сложной формы проще определить экспериментально. Из уравнения (1) получим
Момент инерции тела Iz можно найти по формуле (12), если экспериментально оценить момент сил Mz и угловое ускорение e.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Найдите массу m падающего груза и диаметры D и d шкивов. Установите и измерьте определенную высоту h падающего груза. Запишите найденные результаты в таблицу 1. 2. С помощью кнопки "СЕТЬ" включите экспериментальную установку. 3. Поместите на спицы маятника 4 грузика с массами m1 на одинаковом расстоянии R1 от центра шкива и добейтесь безразличного равновесия. Измерьте R1 и запишите в таблицу 1. 4. В один слой намотайте нить на шкиве с большим диаметром D. Отпустите крестовину и измерьте время падения t1D груза m с высоты h, нажимая кнопку "ПУСК". После измерения нажмите кнопку "СБРОС". Повторите эти измерения не менее пяти раз. Результаты запишите в таблицу 1. 5. Повторите измерения п.4, наматывая нить на шкив меньшего диаметра d, определяя время t1d. 6. Повторите измерения п.п.3¸5 для других расстояний R2, R3 и R4 грузиков до оси вращения. Результаты измерений запишите в таблицу 1. 7. Для каждого расстояния R и диаметра шкива найдите средние значения времени падения Таблица 1
8. Полуширину доверительного интервала
9. Для каждого диаметра шкива постройте график зависимости 10. По формулам (13) и (15) вычислите угловое ускорение 11. Для одного расстояния R1 по формулам (13), (14) и (15) оцените, как меняется угловое ускорение e при изменении момента силы, вызванном изменением радиуса r шкива.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы. 2. Напишите основной закон динамики вращательного движения твердого тела относительно неподвижной оси. 3. Дайте определение момента силы относительно точки (центра). 4. Дайте определение момента силы относительно оси. 5. Найдите момент силы относительно оси Z, если модуль момента этой силы относительно точки О, лежащей на оси, равен М0 = 10 Нм, а направление момента образует с осью Z угол: 1) g = 30°; 2) g = 150°. 6. Модуль радиуса-вектора, проведенного из начала координат О в точку приложения силы, равен r = 30 см, а направление образует с направлением силы угол 7. Определите момент силы относительно точки, если модуль силы равен 8. Дайте определение момента инерции тела относительно оси. 9. По какой формуле можно вычислить момент инерции относительно оси: 10. На каком расстоянии от оси находится материальная точка массой 11. Моменты инерции относительно оси трех тел по отдельности равны 12. Какую массу имеет прямой круглый однородный цилиндр с радиусом основания R = 10 см, если момент инерции цилиндра относительно оси, проходящей через его центр масс параллельно боковой поверхности, равен 13. Сформулируйте теорему Штейнера. 14. Момент инерции однородного шара радиусом R = 6 см относительно оси, проходящей через центр шара, равен Iс. На каком расстоянии от центра шара должна находится ось, чтобы момент инерции шара относительно ее оказался равным 2Iс? 15. Определите угловое ускорение твердого тела, вращающегося 16. Нарисуйте эскиз маятника Обербека. 17. Как можно менять момент инерции маятника Обербека? 18. Момент какой силы сообщает маятнику Обербека угловое ускорение? 19. Почему момент силы тяжести крестовины равен нулю? 20. Какие силы действуют на груз, подвешенный к маятнику Обербека? 21. Как найти силу натяжения нити, на которой подвешен груз? 22. Как определить ускорение груза, подвешенного к маятнику Обербека? 23. Как найти угловое ускорение крестовины? 24. Выведите формулу экспериментального определения момента инерции маятника Обербека. 25. Какие величины постоянны при выполнении эксперимента в данной лабораторной работе? 26. Как применить теорему Штейнера для теоретической оценки момента инерции маятника Обербека? 27. Как меняется угловое ускорение маятника Обербека при удалении грузиков крестовины от оси вращения? 28. Меняется ли натяжение нити в зависимости от расстояния грузиков крестовины от оси вращения? 29. Как меняется угловое ускорение крестовины при изменении радиуса r ее шкива? 30. Выведите формулу вычисления доверительного интервала DI при экспериментальном определении момента инерции I маятника Обербека.
Лабораторная работа № 6
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ ЦЕЛЬ РАБОТЫ Экспериментальное измерение моментов инерции твердых тел с помощью крутильных колебаний. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Укажите цель данной лабораторной работы. 2. Мерой какой величины является момент инерции тела относительно оси? 3. По какой формуле можно вычислить момент инерции относительно оси системы материальных точек? 4. Как вычислить момент инерции произвольного тела относительно оси? 5. Сравните моменты инерции трех тел одинаковой формы и размеров, если одно тело изготовлено из алюминия, другое - из железа, а третье - из свинца. 6. На каком расстоянии от оси находится материальная точка массой m = 10 г, если ее момент инерции относительно этой оси равен I = 4×10-4 кг-м2? 7. Моменты инерции относительно оси О1О2 трех тел по отдельности равны I1 = 5 кг×м2; I2 = 3 кг×м2; I3 = 2 кг×м2. Найдите момент инерции системы указанных тел относительно той же оси О1О2. 8. Какой радиус основания имеет прямой круглый однородный цилиндр массой 9. Какую массу имеет прямой круглый однородный цилиндр 10. Сформулируйте теорему Штейнера. 11. Как найти момент инерции тела относительно оси, не проходящей через центр масс тела? 12. Как момент инерции однородного шара относительно оси зависит от расстояния центра шара до этой оси? 13. Два шара, изготовленные из одного металла, имеют одинаковую массу. Сравните моменты инерции шаров относительно оси, проходящей через их центры, если один из шаров имеет внутри полость. 14. Сравните моменты инерции двух однородных шаров одинаковой массы относительно оси, проходящей через центры шаров, если плотность шаров: 1) одинакова; 2) различается в 2 раза. 15. Нарисуйте эскиз экспериментальной установки. 16. Где помещают изучаемые тела? 17. Какая часть экспериментальной установки совершает крутильные колебания? 18. Для чего в платформе сделаны отверстия? 19. Как найти расстояние от грузика до оси вращения? 20. Как изменится период крутильных колебаний платформы, если ее момент инерции увеличится в 4 раза? 21. Как период крутильных колебаний платформы зависит от коэффициента упругости стержня, на котором она подвешена? 22. Выведите расчетную формулу для определения момента инерции I0 пустой платформы. 23. Какая величина определяется в упражнении 1? 24. Какие измерения проводятся при выполнении упражнения 1? 25. Как находят полуширину доверительного интервала при определении момента инерции пустой платформы? 26. Какой должна быть величина 27. Изменится ли период колебаний и момент инерции платформы, если платформу подвесить не на стальной стержень, а на медный? 28. Что измеряют в упражнении 2? 29. Укажите расчетную формулу для определения момента инерции грузика, центр масс которого находится на расстоянии di от оси вращения крутильных колебаний. 30. Какова последовательность действий при выполнении упражнения №2?
Лабораторная работа №7 ИЗМЕРЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ ЦЕЛЬ РАБОТЫ Измерение и использование метода крутильных колебаний на трифилярном подвесе для измерения моментов инерции твердых тел. Проверка теоремы Штейнера.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Упражнение 1. ИЗМЕРЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ 1. Измерьте расстояние R от точек крепления нитей с платформой П до центра платформы. Измерьте соответствующее расстояние r для шайбы С. Найдите расстояние H между центром масс платформы П и шайбой С. Измерьте массу m0 ненагруженной платформы П, а также массы m1 и m2 исследуемых тел. Запишите результаты измерения этих величин в таблицу. 2. Наблюдая гармонические крутильные колебания ненагруженной платформы П, измерьте секундомером время t0 20 полных колебаний платформы. Колебания будут близки к гармоническим, если амплитуда колебаний jm не будет превышать 5°¸6°. Измерение t0 проводите не менее 5 раз и результаты занесите в таблицу. Найдите среднее значение 3. Положите первое (сплошной диск) тело на платформу так, чтобы центр масс тела располагался над центром платформы. Повторите пункт 2 для платформы П, нагруженной первым телом, т.е. не менее 5 раз наблюдайте время t1 20 полных колебаний и вычислите 4. Положите второе тело (диск, состоящий из двух половинок) на платформу так, чтобы центр масс тела располагался над центром платформы. Повторите пункт 2 для платформы П, нагруженной вторым телом, т.е. не менее 5 раз наблюдайте время t2 20 полных колебаний и вычислите 5. Результаты наблюдений и вычислений занесите в таблицу 1. Таблица 1
6. По формулам (13) и (14) найдите момент инерции I0 ненагруженной платформы и полуширину доверительного интервала DI0. 7. Найдите суммарную массу
I01 платформы с первым телом и полуширину доверительного интервала DI01. Зная I0, DI0, I01, DI01, по формулам (15) и (16) вычислите момент инерции I1 первого тела и полуширину доверительного интервала DI1.
8. Повторите пункт 7 для второго тела (диска, состоящего из двух половинок). Найдите суммарную массу 9. Запишите результаты измерений в форме доверительных интервалов:
Упражнение 2. ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА
10. Выполните упражнение 1, исключив пункты 3 и 7. 11. Поместите на платформу П второе тело, раздвинув его половинки вдоль диаметра АК платформы так, как показано на рис.20. Измерьте расстояние d центра масс второго тела до оси вращения не менее 5 раз. Найдите среднее значение
13. С помощью теоремы Штейнера
14. Представьте результаты наблюдений и вычислений в форме доверительных интервалов:
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы. 2. Дайте определение момента инерции тела относительно оси. 3. По какой формуле можно вычислить момент инерции тела относительно оси: 4. Найдите момент инерции относительно оси материальной точки массой 5. Определите момент инерции относительно оси системы материальных точек с массами m1 = 0,l кг; m2 = 0,2 кг; m3 = 0,3 кг; m4 = 0,7 кг; m5 = 0,8 кг; m6 = 0,9 кг, если каждая точка удалена на расстояние R=0,5 м от этой оси. 6. Найдите момент инерции относительно оси платформы с лежащими на ней двумя дисками, если по отдельности их моменты инерции соответственно равны I1 = 8 кг×м2, I2 = 0,75 кг×м2, I3 = 0,5 кг×м2. 7. Определите момент инерции тонкого обруча массой m = 1 кг и радиусом 8. Какую массу имеет круглый прямой цилиндр с радиусом основания 9. Сформулируйте теорему Штейнера. 10. Моменты инерции тела относительно двух параллельных осей равны 11. Определите момент инерции тонкого обруча радиусом R = 20 м и массой 12. Найдите момент инерции однородного шара массой m = 1 кг и радиусом 13. С каким ускорением вращается однородный шар массой m = 1 кг и радиусом 14. С какой угловой скоростью вращается тело, если его момент инерции относительно оси вращения равен I = 0,01 кг×м2, а кинетическая энергия тела Ек = 20 мДж? 15. Какова цель упражнения 1 данной лабораторной работы? 16. Какая часть экспериментальной установки совершает крутильные колебания? 17. Куда помещают тело, момент инерции которого нужно измерить? 18. Как подвешена подвижная часть экспериментальной установки? 19. Как меняется энергия платформы П при крутильных колебаниях на трифилярном подвесе? 20. Какие измерения проводят при выполнении упражнения 1? 21. Укажите последовательность действий при измерении момента инерции тела с помощью крутильных колебаний на трифилярном подвесе. 22. По какой формуле вычисляют момент инерции пустой или нагруженной платформы? 23. С каким периодом совершаются крутильные колебания, если они описываются уравнением 24. Момент инерции платформы с телом равен I = 2,3×10-2 кг×м2, а момент инерции пустой платформы I0 = 2×10-2 кг×м2. Найдите момент инерции тела. 25. Полуширина доверительного интервала момента инерции платформы с телом равна DI=1,5×10-3 кг×м2, а пустой платформы - DI0 =10-3 кг×м2. Чему равна полуширина доверительного интервала момента инерции одного тела? 26. Какова цель упражнения 2 данной лабораторной работы? 27. Укажите последовательность действий при проверке теоремы Штейнера с помощью крутильных колебаний. 28. По какой формуле в упражнении 2 определяют экспериментальное значение момента инерции испытуемого тела? 29. По какой формуле в упражнении 2 вычисляют теоретическое значение момента инерции испытуемого тела? 30. Почему при выполнении упражнения 2 удобно использовать тело, разрезанное на две половинки?
Лабораторная работа № 8 ЦЕЛЬ РАБОТЫ
Изучение законов, по которым происходит колебательное движение математического и физического маятников, и экспериментальное определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Ускорение свободного падения (ускорение силы тяжести) - ускорение, которое приобретает свободная материальная точка под действием силы тяжести. Такое ускорение имел бы центр тяжести любого тела при падении тела на Землю с небольшой высоты в безвоздушном пространстве. Как и сила тяжести, ускорение свободного падения зависит от широты места и высоты его над уровнем моря [1]. Для установления физического смысла вектора ускорения силы тяжести ( Таким образом, при указанных условиях ускорение свободного падения равно (рис.21):
В каждой точке вектор Если бы Земля была правильным шаром, то угол a между векторами
где j - географическая широта местонахождения точки,
Следует отметить, что для реального земного шара формула (2) достаточно точна. Проецируя векторы
Величина ускорения свободного падения |g| может быть найдена экспериментально, что является целью данной лабораторной работы. По данным [2] ускорение на полюсе gп = 983,2 см/c2, на экваторе Считая, что Земля - правильный шар со сферически - симметричным распределением вещества в нем, можно показать, что ускорение свободного падения на Земной поверхности (на полюсе, где отсутствует центробежная сила, обусловленная суточным вращением Земли) определяется формулой:
отсюда где G = 6,67×10-11 (Н×м2)/кг2 - гравитационная постоянная, М3 = 5,98×1024 кг - масса Земли, R3 = 6,37×106 - средний радиус Земли. Можно показать, что ускорение силы тяжести на высоте h над Землей связано с ускорением g0 следующим соотношением:
При определении ускорения свободного падения на глубине h следует иметь в виду, что тело испытывает притяжение не всей массой Земли, а только слоев, лежащих глубже этого тела. В настоящее время существует ряд прямых и косвенных методов измерений ускорения силы тяжести. Один из способов прямого измерения ускорения силы тяжести по времени падения шарика с известной высоты описан в [10]. Этот способ отличается простотой и наглядностью, но весьма неточен из-за ошибок, причинами возникновения которых являются неодновременность включения электрического секундомера и выключение электромагнита, удерживающего шарик в исходном состоянии, задержка между моментом падения шарика на пластину и разрывом цепи секундомера, что приводит к погрешности измерения времени падения шарика. Большинство косвенных методов измерения ускорения силы тяжести основано на применении формул периода колебаний математического и физического маятников. Прежде чем перейти к рассмотрению методики указанных способов измерения ускорения g, следует напомнить некоторые физические величины и законы (теоремы), которые будут полезны при выполнении данной лабораторной работы (для более детальной проработки нижеследующего материала можно воспользоваться литературными источниками [2,3] и др.). Важнейшие законы механики связаны с понятием момента силы (и момента импульса). Следует различать моменты этих векторов относительно неподвижного центра (точки) и относительно неподвижной оси. В данной лабораторной работе рассматривается только момент силы, поэтому целесообразно напомнить эту величину.
Итак, момент силы Вектор Момент
где
Следует отметить, что момент силы относительно оси не зависит от выбора точки О, лишь бы она находилась на этой оси. Момент силы относительно оси - величина алгебраическая, причем его знак зависит как от выбора положительного направления Z, так и от направления вращения соответствующего момента силы. Для вращательного движения существенное значение имеет распределение массы по объему твердого тела, и инертные свойства твердого тела при вращательном движении определяются моментом инерции. Момент инерции твердого тела относительно оси равен сумме произведений элементарных масс тела на квадраты их расстояний до оси вращения, т.е.
Вычисление момента инерции тела производится по формуле:
где dm и dv - элементарные массы и объем, находящиеся на расстоянии r от оси вращения,
Но во многих случаях определение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси равен моменту инерции Ic относительно оси, параллельно данной и проходящей через центр масс (С) тела, плюс произведение массы (m) тела на квадрат расстояния (d) между осями: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

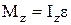 (1)
(1)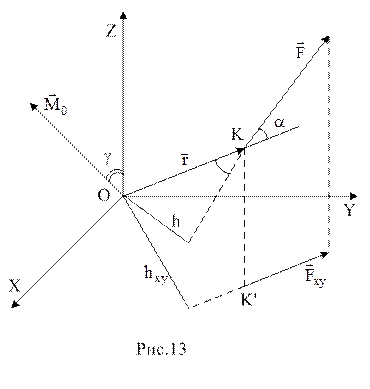 Момент силы характеризует вращательное действие силы. Различают момент силы относительно точки (центра) и момент силы относительно оси. Моментом силы (см.рис.13) относительно точки О называется вектор
Момент силы характеризует вращательное действие силы. Различают момент силы относительно точки (центра) и момент силы относительно оси. Моментом силы (см.рис.13) относительно точки О называется вектор  , равный векторному произведению силы
, равный векторному произведению силы  и радиуса - вектора
и радиуса - вектора  , проведенного из точки О в точку К приложения силы:
, проведенного из точки О в точку К приложения силы: . (2)
. (2)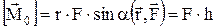 , (3)
, (3) и
и  . (4)
. (4)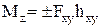 , (5)
, (5) - проекция силы
- проекция силы  , (6)
, (6) - масса материальной точки, удаленной на расстояние Ri от оси z.
- масса материальной точки, удаленной на расстояние Ri от оси z. отдельных материальных точек тела. Если массу
отдельных материальных точек тела. Если массу  выразить через плотность тела r и объема
выразить через плотность тела r и объема  . (7)
. (7) - это интеграл по объему тела V:
- это интеграл по объему тела V: . (8)
. (8) . (9)
. (9) , (10)
, (10)
 . (11)
. (11) . (12)
. (12) груза, а также полуширину доверительного интервала Dt. По формуле (15) вычислите момент инерции I маятника Обербека в каждом случае.
груза, а также полуширину доверительного интервала Dt. По формуле (15) вычислите момент инерции I маятника Обербека в каждом случае.

 . (21)
. (21) .
. для различных R и постройте график зависимости
для различных R и постройте график зависимости  для каждого диаметра шкива. Пренебрегая погрешностями измерения D и h, найдите полуширину De доверительного интервала с помощью формулы:
для каждого диаметра шкива. Пренебрегая погрешностями измерения D и h, найдите полуширину De доверительного интервала с помощью формулы:  .
. , чтобы относительная погрешность результата измерения в упражнении 1 была минимальной?
, чтобы относительная погрешность результата измерения в упражнении 1 была минимальной? и полуширину доверительного интервала
и полуширину доверительного интервала  .
.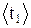 и
и  .
. и
и 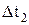 .
.
 платформы и первого тела. Используя
платформы и первого тела. Используя  ,
,  и
и  платформы и второго тела, по формулам (13) и (14) вычислите момент инерции I02 платформы со вторым телом и полуширину доверительного интервала DI02, а по формулам (15) и (16) определите момент инерции I2 второго тела и полуширину доверительного интервала DI2.
платформы и второго тела, по формулам (13) и (14) вычислите момент инерции I02 платформы со вторым телом и полуширину доверительного интервала DI02, а по формулам (15) и (16) определите момент инерции I2 второго тела и полуширину доверительного интервала DI2. ;
;  ;
;  .
. и полуширину доверительного интервала Dd.
и полуширину доверительного интервала Dd. 12. Для второго тела с раздвинутыми половинками (см.рис.20) измерьте время
12. Для второго тела с раздвинутыми половинками (см.рис.20) измерьте время  20 полных колебаний, по формулам (13) и (14) найдите момент инерции
20 полных колебаний, по формулам (13) и (14) найдите момент инерции 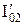 платформы П с раздвинутым вторым телом и полуширину доверительного интервала
платформы П с раздвинутым вторым телом и полуширину доверительного интервала  . По формулам (15) и (16) вычислите момент инерции
. По формулам (15) и (16) вычислите момент инерции 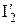 второго тела, смещенного от оси вращения на расстояние d и полуширину доверительного интервала
второго тела, смещенного от оси вращения на расстояние d и полуширину доверительного интервала  .
. вычислите теоретическое значение момента инерции второго тела, смещенного от оси вращения на расстояние d и полуширину доверительного интервала
вычислите теоретическое значение момента инерции второго тела, смещенного от оси вращения на расстояние d и полуширину доверительного интервала  по формуле:
по формуле: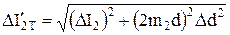 .
. ;
;  . Сравните полученные доверительные интервалы.
. Сравните полученные доверительные интервалы. ?
? ) предположим, что внешние[1] силы отсутствуют и скорость материальной точки равна нулю. Тогда вектор
) предположим, что внешние[1] силы отсутствуют и скорость материальной точки равна нулю. Тогда вектор  , (1)
, (1) где
где  - ускорение, характеризующее гравитационное поле Земли и равное
- ускорение, характеризующее гравитационное поле Земли и равное ,
,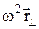 - ускорение, сообщаемое центробежной силой инерции и обусловленное суточным вращением Земли.
- ускорение, сообщаемое центробежной силой инерции и обусловленное суточным вращением Земли. , т.е. различие между направлениями
, т.е. различие между направлениями 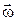 суточного вращения Земли). Сплюснутость Земли (и неравномерность распределения вещества) отражается на различии величины
суточного вращения Земли). Сплюснутость Земли (и неравномерность распределения вещества) отражается на различии величины  , (2)
, (2) .
. . (3)
. (3)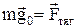 ,
,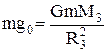 ,
, , (4)
, (4) . (5)
. (5) Момент силы относительно центра (точки) есть вектор. Момент силы относительно оси - это проекция на эту ось его момента относительно точки, лежащей на этой оси, т.е. момент силы относительно оси уже не является вектором.
Момент силы относительно центра (точки) есть вектор. Момент силы относительно оси - это проекция на эту ось его момента относительно точки, лежащей на этой оси, т.е. момент силы относительно оси уже не является вектором.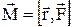 . (6)
. (6) направлен перпендикулярно плоскости векторов
направлен перпендикулярно плоскости векторов  Действительно,
Действительно,  , (7)
, (7) - плечо силы F. Момент силы
- плечо силы F. Момент силы  . (8)
. (8) . (9)
. (9) , (10)
, (10)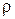 - плотность тела в данной точке.
- плотность тела в данной точке.


