
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение твердого тела с закрепленной осью.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Абсолютно твердым телом называется тело, деформациями которого в данных условиях можно пренебречь. При этом расстояния между любыми двумя точками тела остаются неизменными. При вращении тела с закрепленной осью все точки тела, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. При таком движении путь S, скорость v, ускорение а разных точек тела неодинаковы, поэтому для описания движения неудобно пользоваться этими понятиями. Угол поворота α любой точки тела одинаков и может быть использован как мера перемещения тела. Угловое перемещение
Вектор угловой скорости направлен по оси вращения так же, как и угловое перемещение. Быстроту изменения угловой скорости во времени характеризует угловое ускорение:
Вектор углового ускорения направлен по оси вращения в ту же сторону, что и вектор угловой скорости Найдем связь между линейными и угловыми величинами. Величина линейного перемещения dS точки, вращающейся по окружности радиуса r:
Разделив обе части уравнения (21.3) на
Теперь продифференцируем (20.4) по времени:
где Сформулируем и докажем основной закон динамики твердого тела. Он аналогичен второму закону Ньютона при поступательном движении:
и позволяет определить угловое ускорение твердого тела: угловое ускорение твердого тела прямо пропорционально суммарному моменту внешних сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения
Рассмотрим твердое тело, которое может вращаться вокруг неподвижной оси ОО (рис.21.1). Разобьем это твердое тело на отдельные элементарные массы Δ m i. Равнодействующую всех сил, приложенных к Δ m i, обозначим через F i. Достаточно рассмотреть случай, когда сила F i лежит в плоскости, перпендикулярной оси вращения: составляющие сил, параллельные оси, не могут влиять на вращение тела, так как ось закреплена. Тогда уравнение второго закона Ньютона для касательных составляющих силы и ускорения запишется в виде:
Нормальная составляющая силы
Умножим обе части (21.9) на
Заметим, что F ik r i= F i sinα r i= F i l i, где α – угол между вектором силы F i и радиус-вектором точки r i (рис.21.1), l i – перпендикуляр, опущенный на линию действия силы из центра вращения (плечо силы). Окончательно из (21.10) получим:
Скалярная величина
Векторы
Просуммируем (21.11) по всем элементарным массам, на которые разбито тело:
Здесь учтено, что угловое ускорение всех точек твердого тела одинаково, и его можно вынести за знак суммы. В левой части равенства стоит сумма моментов всех сил (и внешних, и внутренних), приложенных к каждой точке тела. Но по третьему закону Ньютона, силы, с которыми точки тела взаимодействуют друг с другом (внутренние силы), равны по величине и противоположны по направлению и лежат на одной прямой, поэтому их моменты компенсируют друг друга. Таким образом, в левой части (21.14) остается суммарный момент только внешних сил: Сумма произведений элементарных масс на квадрат их расстояний от оси вращения называется моментом инерции твердого тела относительно данной оси:
Таким образом, из (21.14) получим (21.7). Момент инерции В случае непрерывного распределения массы сумма в (21.15) сводится к интегралу по всему объему тела:
Вычислим момент инерции однородного диска плотностью ρ, высотой h, внутренним радиусом R 1 и внешним радиусом R 2 (рис.21.2) относительно оси, проходящей через центр масс перпендикулярно плоскости диска. Разобьем диск на тонкие кольца толщиной dr и высотой h так, что внутренний радиус кольца равен r, внешний – (r+dr) (рис.21.3). Объем такого кольца
Подставим dm в (21.16) и проинтегрируем по r (
Масса диска
В частном случае сплошного диска или цилиндра радиусом R подставим в (21.18) R 1=0, R 2= R и получим:
Если ось вращения не проходит через центр масс тела, вычисления по формуле (21.16) могут быть довольно сложными. В этом случае расчет момента инерции облегчается применением теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции
В данной работе момент инерции тела (платформы) определяется экспериментально методом крутильных колебаний. Рассмотрим общие закономерности колебательного движения крутильного маятника. Испытуемое твердое тело 1, имеющее вид диска радиуса R, подвешено на упругой металлической проволоке 2 (рис.21.4) так, что нижний конец проволоки проходит через центр тяжести диска, а верхний закреплен. При повороте диска на некоторый угол aвокруг оси ОО возникают упругие силы, которые стремятся возвратить диск к положению равновесия. Возвращающий момент сил М обусловлен упругими деформациями, возникающими при закручивании стальной проволоки, с которой скреплена платформа. При малых углах поворота α можно считать, что этот момент сил прямо пропорционален углу поворота, то есть выполняется закон Гука:
где По основному закону динамики вращательного движения (21.7):
где
Уравнение (21.23) можно записать так:
где принято обозначение:
Уравнение вида (21.24) является дифференциальным уравнением гармонических колебаний. Его решением является гармоническая функция:
Здесь ω – круговая частота колебаний, φ 0 – начальная фаза, φ=ωt+φ 0 – фаза колебаний в данный момент времени, α0 – амплитуда колебаний (максимальное значение угла поворота α). Убедимся в том, что (21.26) является решением дифференциального уравнения (21.24) непосредственной подстановкой, вычислив производные:
Из (21.27) следует (21.24). Вообще, если вторая производная по времени какой-либо физической величины пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону, то есть по закону синуса или косинуса. Период крутильныхколебаний, то есть время одного полного колебания, найдем из (21.25):
Из выражения (21.28) находим момент инерции тела:
Для исключения из формулы (21.29) неизвестного модуля кручения К поступают следующим образом. На диск помещают дополнительный груз, момент инерции которого Iгруз относительно оси колебаний известен. При этом полный момент инерции тела с дополнительным грузом станет равным I 1= I+Iгруз, и период T 1 крутильных колебаний изменится:
или:
Поделив почленно (21.31) на (21.29), получим:
откуда окончательно для неизвестного момента инерции платформы:
Экспериментальная часть
Приборы и оборудование: лабораторная установка с секундомером и металлические диски.
Описание установки (вариант 1).
В первом варианте установки (рис.21.4) платформа 1, момент инерции которой требуется определить, подвешена на проволоке 2. На платформу 1 симметрично на расстоянии a от центра помещают три дополнительных груза массой m и радиусом r каждый. Эти три груза относительно оси ОО создают дополнительный момент инерции Iгруз, который находится по теореме Штейнера (21.20) и равен:
Здесь момент инерции одного дополнительного груза относительно оси, проходящей через центр масс, найден из (21.19): Подставив (21.33) в (21.32), для вычисления искомого момента инерции платформы окончательно получим:
Для измерения линейных размеров и расстояний используется штангенциркуль и линейка, время определяется по секундомеру, масса каждого дополнительного груза m= 730 г.
Порядок выполнения работы 1. Исследуемое тело – платформа (без дополнительных грузов) приводится в крутильные колебания. Внимание! Угол закручивания не должен превышать 10-150, иначе можно сломать установку. Кроме того, при больших углах закручивания не выполняется закон Гука (21.21), и колебания не будут гармоническими.
2. На исследуемое тело установить 3 дополнительных груза (диска) и вновь (5 раз) определить время 20 колебаний, найти t 1 ср. и период колебаний:
3. Штангенциркулем измерить радиус дополнительных дисков r и линейкой - расстояние a между осями. Измерения проводятся три раза для каждого из грузов, значения a и r усредняются. 4. Вычислить момент инерции по формуле (21.34). 5. Результаты измерений и вычислений занести в таблицу 21.1. 6. Вычислить абсолютную и относительную погрешности измерений. Замечание 1: погрешность времени
где коэффициент Стьюдента для числа опытов n=5 и доверительной вероятности α=0.95 равен:
Замечание 2: для вычисления относительной погрешности
при этом 7. Сделать выводы по работе.
Таблица 21.1.
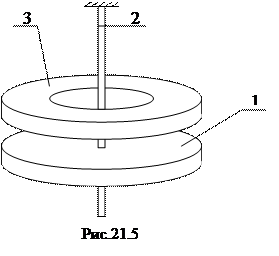
Описание установки (вариант 2). Установка (рис.21.5) состоит из штатива, исследуемого диска 1, закрепленного на проволоке 2, и одного съемного груза в виде диска 3. Ось съемного груза совпадает с осью диска. Для измерения линейных размеров и расстояний используется штангенциркуль и линейка, время определяется по секундомеру. Массу съемного диска необходимо определить из его размеров и плотности.
а момент инерции дополнительного съемного диска из (21.40) и (21.18):
Далее из (21.32) и (21.41) получим расчетную формулу для момента инерции платформы:
Порядок выполнения работы
Исследуемое тело (без дополнительного груза) приводится в крутильные колебания. Внимание! Угол закручивания не должен превышать 10-150, иначе можно сломать установку. Кроме того, при больших углах закручивания не выполняется закон Гука (21.21), и колебания не будут гармоническими. 1. Секундомером измерить время t, которое требуется для совершения 20 полных колебаний, и вычислить период колебаний по формуле (21.35). Опыт повторить 5 раз. 2. На исследуемое тело установить дополнительный диск и вновь (5 раз) определить время 20 колебаний, найти t 1 ср. и период колебаний (21.36). 3. Линейкой и (или) штангенциркулем измерить внешний R 2 и внутренний R 1 радиусы дополнительного диска и его толщину h (рис.21.2). Вычислить момент инерции по формуле (21.42). 4. Результаты измерений и вычислений занести в таблицу по форме 21.2:
Форма 21.2.
5. Вычислить абсолютную и относительную погрешности измерений. Замечание: для вычисления относительной погрешности I можно воспользоваться формулой:
при этом I рассчитывается по усредненным значениям периода; либо I рассчитывается в каждом из пяти опытов, затем усредняется, и погрешность ΔI рассчитывается как погрешность случайной величины, аналогично формуле (21.37). Можно рассчитать погрешность обоими способами и сравнить результаты. Сделать выводы по работе.
Контрольные вопросы
1. Дайте определение углового перемещения, угловой скорости и ускорения. Как направлены эти вектора? 2. Запишите формулы, связывающие линейные и угловые величины перемещения, скорости, ускорения. 3. Что такое момент силы относительно оси? От чего он зависит? Как направлен вектор момента силы? 4. Что такое момент инерции материальной точки, твердого тела, от чего он зависит? 5. Сформулируйте и докажите второй закон Ньютона для вращательного движения (21.7). 6. Выведите дифференциальное уравнение крутильных колебаний (21.24). 7. Докажите, что выражение (21.26) является решением дифференциального уравнения (21.24). 8. Какие колебания являются гармоническими? 9. Что такое период колебаний, частота колебаний? 10. Сформулируйте теорему Штейнера и покажите, где в работе она используется. 11. Можно ли пользоваться расчетными формулами в этой работе, если углы отклонения крутильных колебаний будут большими? Почему? 12. Докажите формулы (21.39) и (21.43).
Используемая литература
[5] §2.8, 7.1, 19.1, 19.2; [3]§4.1-4.3, 27.1, 27.2; [1]§36-39, 52, 53; [6]§1.4, 1,31-1.34, 3.3, 3.6; [7] §2,3 4, 16, 17, 18, 19, 140, 141, 142.
Лабораторная работа 1-22 “Определение отношения удельных теплоемкостей для воздуха методом адиабатического расширения”
Цель работы: усвоить термодинамические величины, характеризующие состояние идеального газа; определить отношение удельных теплоемкостей C p/ C v для воздуха Теоретическое введение
Теплота
Уравнение (22.1) – первое начало термодинамики. Символ При поглощении веществом теплоты
Так как величина Для газов эти величины связаны друг с другом простым образом. По определению
Из (22.1)
Отсюда следует, что теплоемкости
можно рассматривать как определения. Они позволяют найти Каждое состояние термодинамической системы характеризуется совокупностью значений физических величин, отражающих ее свойства. Величины, имеющие простую физическую природу и допускающие непосредственное измерение (давление
У идеальных газов особенно простое уравнение состояния
где Используя определение теплоемкости (22.3), первое начало термодинамики и уравнение состояния для газов, можно записать для идеальных газов в расчете на один моль:
так как Если применить первое начало термодинамики (22.1) для описания адиабатического расширения (сжатия) идеального газа (
Из него следует, что при адиабатическом процессе температура
Это равенство называется уравнением Пуассона. Еще одно уравнение для адиабатического процесса связывает параметры
Величина
Экспериментальная часть
Описание установки и методика измерения
В работе определение отношения
и уравнения адиабатического процесса
соблюдающихся для идеального газа. В равенствах (22.10) и (22.11) Исследуются параметры идеального газа, последовательно проходящего через три состояния. Вначале с помощью насоса необходимо по возможности быстро накачать небольшое количество воздуха в баллон при закрытом кране 3. Через 2-3 мин. температура воздуха в баллоне понизится до температуры окружающей среды Если теперь открыть кран 3 быстро, на несколько секунд, то баллон соединяется с атмосферой. Практически сразу давление воздуха в баллоне станет равным атмосферному Затем кран 3 закрыть. Давление газа в баллоне начнет возрастать, так как охладившийся при адиабатическом расширении воздух станет снова нагреваться. Воздух нагревается изохорически до комнатной температуры На рис.22.2 показаны адиабата (1-2) и изохора (2-3). Состояние газа 1 и 3 имеют одну и ту же температуру Переход (1-2) из первого состояния во второе описывается уравнением Пуассона (22.9), которое в нашем случае следует записать так:
здесь Сравнивая конечное, третье состояние с первым, видим, что температура газа в этих состояниях одинакова. Значит, к переходу (1-3) применим закон Бойля – Мариотта.
Возведя полученное равенство (22.13) в степень
Так как
Рис. 22.2 Необходимо отметить, что на опыте не удается осуществить совпадение момента перекрытия крана с окончанием адиабатического расширения (состояние 2). Если кран закрыть раньше, чем давление упадет до атмосферного (на рис 22.2 пунктирная линия; в нашем случае Адиабатический переход газа из состояния 1 в состоянии 2 происходит за какое-то время
где | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 – это вектор, направленный по оси вращения по правилу буравчика, модуль которого равен углу поворота тела за время
– это вектор, направленный по оси вращения по правилу буравчика, модуль которого равен углу поворота тела за время 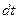 . Угловая скорость характеризует быстроту вращения и равна производной по времени от углового перемещения:
. Угловая скорость характеризует быстроту вращения и равна производной по времени от углового перемещения: . (21.1)
. (21.1) . (21.2)
. (21.2) , если величина угловой скорости увеличивается, и в сторону, противоположную
, если величина угловой скорости увеличивается, и в сторону, противоположную  . (21.3)
. (21.3)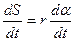 . Так как производная пути по времени – это величина скорости:
. Так как производная пути по времени – это величина скорости:  , а
, а  (21.1), то:
(21.1), то: . (21.4)
. (21.4)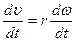 , или:
, или: , (21.5)
, (21.5)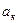 – касательное (тангенциальное) ускорение, определяющее быстроту изменения модуля скорости
– касательное (тангенциальное) ускорение, определяющее быстроту изменения модуля скорости  :
: 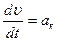 .
. (21.6)
(21.6) . (21.7)
. (21.7) Моментом силы относительно оси называется вектор, направленный по оси вращения и связанный с направлением силы правилом буравчика, модуль которого равен произведению силы на ее плечо:
Моментом силы относительно оси называется вектор, направленный по оси вращения и связанный с направлением силы правилом буравчика, модуль которого равен произведению силы на ее плечо:  . Плечо силы
. Плечо силы  относительно оси вращения – это кратчайшее расстояние от линии действия силы до оси вращения.
относительно оси вращения – это кратчайшее расстояние от линии действия силы до оси вращения. . (21.8)
. (21.8) обеспечивает центростремительное ускорение и на угловое ускорение не влияет. Из (21.5):
обеспечивает центростремительное ускорение и на угловое ускорение не влияет. Из (21.5):  где
где  – радиус вращения i-той точки. Тогда
– радиус вращения i-той точки. Тогда . (21.9)
. (21.9) . (21.10)
. (21.10) . (21.11)
. (21.11)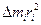 , равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси ОО:
, равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси ОО: . (21.12)
. (21.12)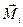 и
и 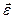 совпадают по направлению с осью вращения, связаны с направлением вращения по правилу буравчика, поэтому равенство (21.11) можно переписать в векторной форме:
совпадают по направлению с осью вращения, связаны с направлением вращения по правилу буравчика, поэтому равенство (21.11) можно переписать в векторной форме: . (21.13)
. (21.13) . (21.14)
. (21.14)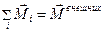 .
. . (21.15)
. (21.15) твердого тела является мерой инертных свойств твердого тела при вращательном движениии аналогичен массе тела во втором законе Ньютона. Он существенно зависит не только от массы тела, но и от ее распределения относительно оси вращения (в направлении, перпендикулярном оси).
твердого тела является мерой инертных свойств твердого тела при вращательном движениии аналогичен массе тела во втором законе Ньютона. Он существенно зависит не только от массы тела, но и от ее распределения относительно оси вращения (в направлении, перпендикулярном оси). . (21.16)
. (21.16) , где
, где  – площадь основания тонкого кольца. Его масса:
– площадь основания тонкого кольца. Его масса: . (21.17)
. (21.17) ):
):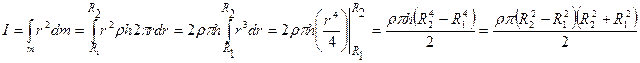
 , тогда окончательно:
, тогда окончательно: . (21.18)
. (21.18) . (21.19)
. (21.19)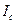 тела относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела на квадрат расстояния
тела относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела на квадрат расстояния 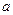 междуосями:
междуосями:
 . (21.20)
. (21.20) , (21.21)
, (21.21) – коэффициент пропорциональности, называемый модулем кручения, величина которого зависит от материала проволоки и ее размеров. Знак «–» показывает, что момент упругих сил возвращает тело к положению равновесия, то есть векторы момента сил
– коэффициент пропорциональности, называемый модулем кручения, величина которого зависит от материала проволоки и ее размеров. Знак «–» показывает, что момент упругих сил возвращает тело к положению равновесия, то есть векторы момента сил  и углового перемещения
и углового перемещения  направлены в противоположные стороны, их проекции на ось вращения имеют противоположные знаки.
направлены в противоположные стороны, их проекции на ось вращения имеют противоположные знаки. , (21.22)
, (21.22)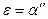 – угловое ускорение. Из (21.2), (21.21) и (21.22) получаем уравнение для угла поворота α:
– угловое ускорение. Из (21.2), (21.21) и (21.22) получаем уравнение для угла поворота α: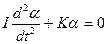 . (21.23)
. (21.23)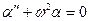 , (21.24)
, (21.24)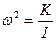 , или:
, или: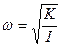 . (21.25)
. (21.25)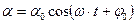 . (21.26)
. (21.26)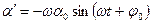 ;
; . (21.27)
. (21.27) . (21.28)
. (21.28) . (21.29)
. (21.29) , (21.30)
, (21.30) . (21.31)
. (21.31) ,
, . (21.32)
. (21.32) . (21.33)
. (21.33) .
. . (21.34)
. (21.34)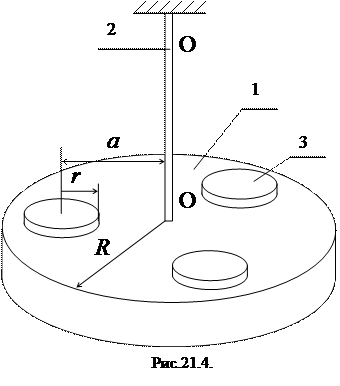 Секундомером измерить время t, которое требуется для совершения 20 полных колебаний. Опыт повторить 5 раз, найти среднее время tср и вычислить период колебаний:
Секундомером измерить время t, которое требуется для совершения 20 полных колебаний. Опыт повторить 5 раз, найти среднее время tср и вычислить период колебаний: . (21.35)
. (21.35) . (21.36)
. (21.36) рассчитывается по стандартной методике расчета погрешностей случайной величины:
рассчитывается по стандартной методике расчета погрешностей случайной величины: , (21.37)
, (21.37) . При этом погрешность периода колебаний из (21.35):
. При этом погрешность периода колебаний из (21.35):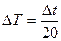 . (21.38)
. (21.38) , (21.39)
, (21.39) Δ I рассчитывается как погрешность случайной величины, аналогично (21.37). Можно рассчитать погрешность обоими способами и сравнить результаты.
Δ I рассчитывается как погрешность случайной величины, аналогично (21.37). Можно рассчитать погрешность обоими способами и сравнить результаты.
 Масса диска
Масса диска  (плотность стали ρ =7800 кг/м3), а его объем
(плотность стали ρ =7800 кг/м3), а его объем  , тогда
, тогда , (21.40)
, (21.40) . (21.41)
. (21.41) . (21.42)
. (21.42)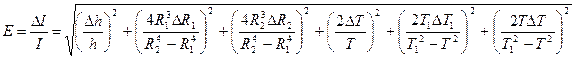 , (21.43)
, (21.43)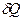 , приданная системе (телу), расходуется на изменение ее внутренней энергии
, приданная системе (телу), расходуется на изменение ее внутренней энергии  и на совершение работы
и на совершение работы 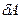 .
. (22.1)
(22.1) (в некоторых учебниках используется обозначение
(в некоторых учебниках используется обозначение 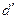 ) указывает на то, что бесконечно малые изменения
) указывает на то, что бесконечно малые изменения  и работа
и работа  зависят от пути процесса. Только внутренняя энергия
зависят от пути процесса. Только внутренняя энергия  является функцией состояния и от пути процесса не зависит.
является функцией состояния и от пути процесса не зависит. называется теплоемкостью вещества
называется теплоемкостью вещества 
 (22.2)
(22.2)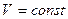 ) – изохорический и при постоянном давлении (
) – изохорический и при постоянном давлении (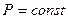 ) – изобарический. Соответствующие им теплоемкости обозначают
) – изобарический. Соответствующие им теплоемкости обозначают  и
и  .
. ,
, 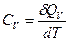 (22.3)
(22.3) ,
,  – энтальпия или теплосодержание.
– энтальпия или теплосодержание. , так как при
, так как при  ,
,  .
. и
и  есть частные производные от энтальпии и внутренней энергии по температуре (при постоянных давлении и объеме). Уравнения
есть частные производные от энтальпии и внутренней энергии по температуре (при постоянных давлении и объеме). Уравнения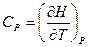 и
и  (22.4)
(22.4) и
и  или
или  .
.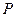 , температура
, температура 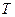 , объем системы
, объем системы  ), используют в качестве параметров состояния. Уравнением состояния называют выражение, связывающее эти параметры. Для однородных систем постоянного состава оно имеет вид
), используют в качестве параметров состояния. Уравнением состояния называют выражение, связывающее эти параметры. Для однородных систем постоянного состава оно имеет вид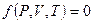 (22.5)
(22.5) , (22.6)
, (22.6) – объем одного моля;
– объем одного моля;  – универсальная газовая постоянная.
– универсальная газовая постоянная.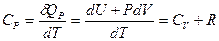 , (22.7)
, (22.7) . Уравнение (22.7) называют соотношением Майера.
. Уравнение (22.7) называют соотношением Майера. ; изменение состояния без теплообмена), учитывая определения:
; изменение состояния без теплообмена), учитывая определения: ,
,  ,
,  и введя обозначение
и введя обозначение  (адиабатическая постоянная), то получим уравнение
(адиабатическая постоянная), то получим уравнение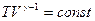 (22.8)
(22.8) остается постоянным. Поскольку
остается постоянным. Поскольку  всегда больше единицы, то
всегда больше единицы, то  и, адиабатическое расширение сопровождается охлаждением, а сжатие – нагреванием газа. Комбинируя уравнение (22.8) с (22.6), можно получить соотношение, связывающее параметры
и, адиабатическое расширение сопровождается охлаждением, а сжатие – нагреванием газа. Комбинируя уравнение (22.8) с (22.6), можно получить соотношение, связывающее параметры  (22.9)
(22.9)
 Экспериментальная установка (рис. 22.1) состоит из стеклянного баллона 1 соединенного с открытым U-образным водяным манометром 2 и имеющего кран 3. Кран позволяет баллону сообщаться с атмосферой. К баллону подсоединен нагнетательный воздушный насос.
Экспериментальная установка (рис. 22.1) состоит из стеклянного баллона 1 соединенного с открытым U-образным водяным манометром 2 и имеющего кран 3. Кран позволяет баллону сообщаться с атмосферой. К баллону подсоединен нагнетательный воздушный насос. производится классическим методом Клемана и Дезорма, основанным на использовании уравнения изотермического процесса
производится классическим методом Клемана и Дезорма, основанным на использовании уравнения изотермического процесса (22.10)
(22.10)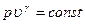 (22.11)
(22.11) обозначает по прежнему давление, а
обозначает по прежнему давление, а  - удельный объем газа.
- удельный объем газа.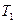 , газ придет в состояние равновесия. Об этом можно судить по прекращению изменений показаний манометра. В этих условиях берется отсчет разности уровней
, газ придет в состояние равновесия. Об этом можно судить по прекращению изменений показаний манометра. В этих условиях берется отсчет разности уровней  в обоих коленах манометра. Обозначим для первого данного состояния газа его удельный объем
в обоих коленах манометра. Обозначим для первого данного состояния газа его удельный объем 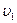 , давление
, давление  , температуру
, температуру 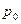 - атмосферное давлении,
- атмосферное давлении,  мм водяного столба).
мм водяного столба). . Второе состояние газа характеризуется параметрами:
. Второе состояние газа характеризуется параметрами:  - новый удельный объем,
- новый удельный объем,  атмосферное давление и
атмосферное давление и  ).
). . Параметры газа в этом третьем состоянии: давление
. Параметры газа в этом третьем состоянии: давление  , удельный объем
, удельный объем  (ни масса, ни объем газа при последних изменениях не менялись), температура
(ни масса, ни объем газа при последних изменениях не менялись), температура  .
.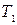 . Следовательно, точки 1 и 3 должны находиться на одной изотерме (1-3).
. Следовательно, точки 1 и 3 должны находиться на одной изотерме (1-3). или
или  (22.12)
(22.12)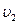 - удельные объемы газа до и после расширения.
- удельные объемы газа до и после расширения. или
или  (22.13)
(22.13) (22.14)
(22.14) и
и  , то можно воспользоваться приближенной формулой
, то можно воспользоваться приближенной формулой  и записать (22.14) в виде
и записать (22.14) в виде (22.15)
(22.15)
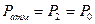 ), то получим завышенное значение
), то получим завышенное значение  . Наоборот, при запаздывании получается заниженное значение
. Наоборот, при запаздывании получается заниженное значение  и чем больше время запаздывания
и чем больше время запаздывания  , тем сильнее
, тем сильнее  отличается от равновесного значения
отличается от равновесного значения  (22.16)
(22.16)


