
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1-15 “Определение коэффициента вязкости жидкости методом Стокса”.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: ознакомление с методом Стокса и определение коэффициента вязкости различных жидкостей.
Теоретическое введение
Во всех реальных жидкостях и газах при перемещении одного слоя относительно другого возникают силы трения. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряющая сила. Наоборот, со стороны слоя, движущегося медленнее, на более быстрый слой действует тормозящая сила. Эти силы, носящие название сил внутреннего трения, направлены по касательной к поверхности слоёв.
которая показывает, как быстро меняется скорость при переходе от слоя к слою, называется градиентом скорости. Величина силы внутреннего трения
где Единицей измерения коэффициента вязкости в СИ служит такая вязкость, при которой градиент скорости, равный 1 м/с на 1м, приводит к силе внутреннего трения в 1 Н на 1 м2 площади слоев. Эта единица называется паскаль-секундой (Па.с). В некоторые формулы (например, число Рейнольдса, формула Пуазейля) входит отношение коэффициента вязкости к плотности жидкости ρ. Это отношение получило название коэффициента кинематической вязкости
Для жидкостей, течение которых подчиняется уравнению Ньютона (15.1), вязкость не зависит от градиента скорости. Такие жидкости называются ньютоновскими. К неньютоновским (то есть не подчиняющимся уравнению (15.1)) жидкостям относятся жидкости, состоящие из сложных и крупных молекул, например, растворы полимеров. Вязкость данной жидкости сильно зависит от температуры: при изменениях температуры, которые сравнительно нетрудно осуществить на опыте, вязкость некоторых жидкостей может изменяться в миллионы раз. При понижении температуры вязкость некоторых жидкостей настолько возрастает, что жидкость теряет текучесть, превращаясь в аморфное твердое тело. Я.И. Френкель вывел формулу, связывающую коэффициент вязкости жидкости с температурой:
Значения коэффициентов вязкости газов существенно меньше, чем жидкостей. С повышением температуры вязкость газа увеличивается (рис.15.2) и при критической температуре становится равной вязкости жидкости. Отличие в характере поведения вязкости при изменении температуры указывает на различие механизма внутреннего трения в жидкостях и газах. Молекулярно-кинетическая теория объясняет вязкость газов переносом импульса из одного слоя в другой слой, происходящим за счет переноса вещества при хаотическом движении молекул газа. В результате в слое газа, движущемся медленно, увеличивается доля быстрых молекул, и его скорость (средняя скорость направленного движения молекул) возрастает. Слой газа, движущийся медленно, увлекается более быстрым слоем, а слой газа, движущийся с большей скоростью, замедляется. С повышением температуры интенсивность хаотического движения молекул газа возрастает, и вязкость газа увеличивается. Вязкость жидкости имеет другую природу. В силу малой подвижности молекул жидкости перенос импульса из слоя в слой происходит из-за взаимодействия молекул. Вязкость жидкости в основном определяется силами взаимодействия молекул между собой (силами сцепления). С повышением температуры взаимодействие молекул жидкости уменьшается, и вязкость также уменьшается. Несмотря на различную природу, вязкость жидкостей и газов с макроскопической точки зрения описывается одинаковым уравнением (15.1). Величину импульса
Из (15.1) и (15.4) получим:
Тогда физический смысл коэффициента динамической вязкости можно сформулировать так: коэффициент вязкости численно равен импульсу, перенесенному между слоями жидкости или газа единичной площади за единицу времени при единичном градиенте скорости. Знак «минус» показывает, что импульс переносится из более быстрого слоя в более медленный. При движении тела в вязкой среде возникают силы сопротивления. Происхождение этого сопротивления двояко. При небольших скоростях, когда за телом нет вихрей (то есть обтекание тела ламинарное), сила сопротивления обуславливается вязкостью среды. Между движущимся телом и средой существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы прилипая к телу. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т.д. Совсем далекие от тела слои можно считать покоящимися. Для ламинарного потока сила трения пропорциональна скорости тела:
где Второй механизм сил сопротивления включается при больших скоростях движения тела, когда поток становится турбулентным. При увеличении скорости тела вокруг него возникают вихри. Часть работы, совершаемой при движении тела в жидкости или газе, идет на образование вихрей, энергия которых переходит во внутреннюю энергию. При турбулентном потоке в некотором интервале скоростей сила сопротивления пропорциональна квадрату скорости тела:
Экспериментальная часть
Приборы и оборудование: лабораторная установка, микрометр, линейка, штангенциркуль, секундомер, шарики. Метод определения
Этот метод основан на измерении скорости установившегося движения твердого шарика в вязкой среде под действием постоянной внешней силы, в простейшем случае – силы тяжести. Выведем рабочую формулу для определения коэффициента вязкости методом Стокса. Если взять шарик большей плотности, чем плотность жидкости, то он будет тонуть, опускаясь на дно сосуда. На падающий шарик действуют три силы (рис.15.3): 1. сила вязкого трения F С по закону Стокса (15.6), направленная вверх, навстречу скорости: F С= 6 πηr v; 2. сила тяжести, направленная вниз:
где
3. выталкивающая сила F Арх, согласно закону Архимеда, равная весу вытесненной жидкости: F Арх = Vρ ж g, (15.9) где Запишем уравнение движения (второй закон Ньютона) для падающего шарика в проекциях на вертикальную ось: ma=F тяж– F Арх– F С. (15.10) Сила тяжести и выталкивающая сила не зависят от скорости движения шарика. Сила трения в законе Стокса прямо пропорциональна скорости. Поэтому на некотором начальном участке l0 (рис.15.3) падения шарика в жидкости, пока скорость мала, сила трения меньше разности сил тяжести и выталкивающей, и шарик в результате движется с ускорением. Величину участка l0 можно оценить из уравнения движения (см. дальше). По мере нарастания скорости падения шарика растет сила вязкого трения. С момента достижения равенства F С = F тяж – F Арх (15.11) сумма сил, действующих на шарик, становится равной нулю, и шарик, в соответствии с первым законом Ньютона, движется по инерции равномерно, с набранной им к этому моменту скоростью. По измеренной скорости установившегося падения шарика можно найти коэффициент вязкости жидкости η. После подстановки в (15.11) выражений (15.6-15.9) получим:
после сокращения и замены радиуса
или:
Из (15.12) выразим коэффициент динамической вязкости:
Наконец, скорость v шарика выражаем через пройденный путь
Выведенная формула (15.14) для расчета коэффициента вязкости, как и формула Стокса (15.6), получены в предположении, что шарик движется в сосуде неограниченного объема. При движении шарика по оси цилиндрического сосуда конечного диаметра D в формуле (14) необходимо учесть влияние стенок сосуда. Уточненная рабочая формула имеет вид:
где Описание установки.
Установка состоит из высокого цилиндрического прозрачного сосуда 1 (рис.15.3), по высоте которого на стенке нанесены на определенном расстоянии друг от друга метки 2. В сосуд налита исследуемая жидкость 3 с известной плотностью. Для определения ее вязкости в верхней части сосуда вблизи центра в жидкость опускают маленькие шарики 4, плотность которых несколько больше плотности жидкости.
Порядок выполнения работы
Упражнение 1. Определение коэффициента вязкости жидкости без учета влияния стенок сосуда.
1. Штангенциркулем измерить диаметр d шарика. 2. Пинцетом или смоченной палочкой опустить шарик по центру сосуда. 3. Определить при помощи секундомера время 4. Измерить линейкой расстояние между метками 5. Рассчитать коэффициент вязкости по формуле (15.14) в каждом опыте. Плотность жидкостей и плотность шарика взять в приложении. 6. Найти среднее значение коэффициента вязкости и рассчитать погрешность
Упражнение 2. Определение коэффициента вязкости жидкости по уточненной формуле с учетом влияния стенок сосуда.
1. Измерить линейкой внутренний диаметр 2. Рассчитать коэффициент вязкости жидкости по формуле (15.15). 3. Сравнить результаты, полученные по формулам (15.14) и (15.15) и сделать выводы. 4. Все результаты занести в таблицу по форме 15.1.
Форма 15.1.
Замечание. Погрешность коэффициента вязкости Δη рассчитывается двумя способами: а) по стандартной методике расчета погрешностей случайной величины:
где коэффициент Стьюдента для числа опытов б) исходя из формулы (15.14) по стандартной методике расчета погрешностей при косвенных измерениях:
где Расчет по (15.17) производится для одного какого-либо опыта, при этом в качестве
Упражнение 3. Оценка участка неравномерного падения шарика l 0. Выведем формулу для оценки l 0. Запишем формулу (15.10): ma=F тяж– F Арх– F С. (15.10) после подстановки выражений (15.6-15.9) получим: ρ ш или после почленного деления на ρ ш
и далее после сокращения и элементарных преобразований и с учетом того, что ускорение – это производная скорости по времени
Решением дифференциального уравнения (15.18) будет функция:
где vр – скорость равномерного (установившегося) движения, v0 – начальная скорость шарика, которую можно принять равной нулю, коэффициент b в показателе степени экспоненты равен:
Убедиться в том, что (15.19) является решением уравнения (15.18), можно путем подстановки (15.19) в (15.18), рассчитав предварительно производную скорости v по времени; при этом будут получены также и выражение для b (15.20), и формула для установившейся скорости движения (см.(15.13)):
Заметим, что (15.19) удовлетворяет начальным условиям: при t= 0 скорость равна v0, при t →∞ скорость v→vр. Движение можно считать практически равномерным, если экспонента мала:
Это реализуется при (bt)→∞, то есть если t >> b -1. Достаточно потребовать (bt)=4; в этом случае отличие скорости от установившейся составит не более 2% (при v0=0):
Далее, с учетом того, что
откуда с учетом (15.20) и (15.21):
и окончательно:
1. Оценить участок неравномерного движения шарика по формуле (15.22). 2. Записать результат в таблицу 15.1. 3. Сравнить полученное значение с величиной l0, реально используемой в установке. 4. Сделать вывод. Контрольные вопросы.
1. Запишите формулу Ньютона для коэффициента динамической вязкости. Сделайте поясняющий рисунок. 2. Что называется коэффициентом динамической вязкости? Поясните его физический смысл и выведите его размерность. 3. Объяснить механизм внутреннего трения для газов и жидкостей. Как зависит от температуры вязкость газов и жидкостей? Почему? 4. Какие силы действуют на шарик, падающий в жидкости? Сделайте рисунок, запишите второй закон Ньютона для шарика, падающего в вязкой жидкости. 5. Почему, начиная с некоторого момента, шарик движется равномерно? 6. Как зависит скорость падения шарика от его диаметра? 7. Имеет ли смысл использование уточненной формулы (15.15) при выполнении работы на данной установке? 8. Выведите приближенную расчетную формулу (15.14) для коэффициента вязкости. 9. Докажите (15.19) и (15.20). Используемая литература
[5] §9.4; [3] §10.7, 10.8; [1] §75, 76, 78, 130; [6] §5.6, 5.7; [7] §31, 33, 48.
Лабораторная работа 1-16 “Определение модуля Юнга методом прогиба”
Цель работы: определение модуля Юнга материала путем измерения прогиба стержня при нагрузке.
Теоретическое введение
Прочность, долговечность и надежность металлических изделий (твердых тел), работающих в различных условиях, во многом зависит от характеристик, определяющих упругие свойства материалов. Твердые тела при этом будем рассматривать как сплошную среду с определенной плотностью
где Деформация называется упругой, если после снятия нагрузки полностью восстанавливаются размеры и форма тела, т.е. это обратимая деформация. Сдвигом называется такая деформация твердого тела, при которой все его плоские слои, параллельные некоторой неподвижной плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Деформация сдвига характеризуется величиной относительного сдвига. При малых деформациях сдвига относительный сдвиг есть просто измеренный в радианах угол При деформации однородного сдвига величина Растяжение тела всегда сопровождается соответствующим сокращением его поперечного сечения и, наоборот, сжатие – соответствующим увеличением поперечного сечения. Характеристикой этого изменения поперечных размеров при растяжении и сжатии является относительное поперечное расширение или сжатие:
где Ясно, что знак продольной деформации
называют коэффициентом Пуассона. Он не зависит от размеров тел и для всех тел, сделанных из данного материала, является константой, характеризующей его свойства. Для всех известных в природе тел коэффициент Пуассона имеет значение в пределах от 0 до 0,5. Деформацию реальных твердых тел представляют в виде диаграммы. При этом удобно растяжение задавать не силой как таковой, а отношением силы к площади сечения:
 (16.4) (16.4)
Величина
где Напряжение, соответствующее точке А, называется пределом пропорциональности Далее (за т.А’) начинается область текучести материала (пластическая деформация) – наибольшие деформации, которым подвергся материал, почти целиком сохраняются как остаточные, но целость материала еще не нарушается. При еще больших нагрузках наступает разрушение. Область упругих деформаций обычно очень незначительна (например, для стали пределу упругости соответствует значение В отличие от растяжения и сжатия деформация сдвига вызывается касательными напряжениями
где При малых деформациях закон Гука в этом случае имеет вид, аналогичный (16.5):
где Итак, упругие свойства деформируемого упругого тела характеризуются двумя основными модулями упругости – модулем Юнга и модулем сдвига
Из (16.8), кстати, следует, что
Экспериментальная часть
В работе определяется модуль упругости предложенных образцов и проверяется зависимость деформации от нагрузки. Используется установка, которая показана на рис. 16.2.
Рис. 16.2. Изгиб представляет собой более сложный вид деформации, чем деформация растяжения или сжатия, так как заключает в себе одновременно и растяжение, и сжатие. Различные слои образца при изгибе несут неодинаковую нагрузку. В большинстве случаев испытания на изгиб проводятся сосредоточенной нагрузкой на образец, лежащий на двух опорах. Образцы изготовляют обычно в виде стержней прямоугольного сечения. Длина образца на 40-60 мм больше, чем расстояние между опорами. Ширина образца должна быть вдвое больше его толщины. На исследуемый образец надевается подвеска для грузов, а образец кладется на острые металлические опоры. Подвеска с грузами находится на одинаковом расстоянии от точек опоры стержня. Стрела прогиба h образца измеряется индикатором часового типа. Если к середине стержня (рис. 16.2), опирающегося концами на неподвижные опоры, приложить вертикальную силу, направленную перпендикулярно оси стержня, то будет наблюдаться деформация изгиба (на рис. 16.2 деформации представлены не в масштабе). Нижние слои стержня при этом испытывают деформацию растяжения, верхние - деформацию сжатия, а средний слой, длина которого не изменяется, нагрузок не несет и называется нейтральным. При так называемом чистом изгибе напряжения, которые испытывают слои материала при деформации, имеют прямую зависимость от их деформации: сжатию соответствуют отрицательные напряжения, растяжению - положительные. Величина прогиба при этом оказывается обратно пропорциональной модулю Юнга
где: F – приложенная к образцу сила,
Лабораторная установка
Схема установки для определения модуля Юнга по прогибу представлена на рис. 16.3.
Рис. 16.3
На основании 1 закреплена массивная направляющая 2. По ней могут перемещаться стойки 3 и кронштейн 4, зажимаемые в необходимом положении винтами 5 (вручную). Стойки вверху оканчиваются призмами 6, на параллельные острия которых устанавливается измеряемый образец 7. В гнезде 8 кронштейна зажимается вручную винтом 9 индикатор перемещения 10. На образце напротив индикатора подвешена серьга 11 с платформой для специальных (с прорезью) гирь 12. При нагружении платформы гирями образец прогибается. Стрела прогиба 13 регистрируется перемещением стрелки индикатора. Методика измерений 1. Ослабив винты 5, установите призмы 6 на заданное (преподавателем) расстояние. Закрепите винты. 2. Установите кронштейн 4 на одинаковом расстоянии от стоек. Закрепите винты. 3. Расположите образец на призмах так, чтобы гнездо индикатора находилось над средней частью по ширине образца. 4. Вставьте индикатор в гнездо, осторожно утопив его так, чтобы стрелка малой шкалы оказалась около метки 5 мм. Аккуратно зажмите индикатор винтом 9. 5. Измерьте штангенциркулем толщину b и ширину a образца. Измерьте линейкой расстояние между ребрами призм l. Установите поворотом кольца нуль на индикаторе. 6. Аккуратно поставьте на платформу гирю. Запишите (по красной шкале) показания индикатора. 7. Снимите с платформы гирю. Если стрелка сместилась с нулевой отметки, установить нуль. Повторите для контроля несколько раз измерения с тем же грузом. 8. Проведите аналогично п.7 измерение прогиба с гирями большей массы (массы брать около 1,2,3,4,5 кг). 9. Результаты занести в таблицу предложенной формы 16.1.
Форма 16.1.
10. Рассчитайте модуль Юнга при каждом измерении и усредните результат. 11. Рассчитайте ошибку определения модуля Юнга D E (достаточно рассчитать для одного опыта). 12. Значения модуля Юнга, совпадающие с учетом ошибки D E друг с другом, т.е. не выходящие за границы значений (E cp + D E)и (E cp - D E), позволяют определить истинное (среднее) значение модуля Юнга. 13. С учетом п.12 определить среднее значение модуля Юнга. 14. Ошибка модуля Юнга D E определяется из рабочей формулы (16.9) как сумма частных ошибок всех величин, входящих в выражение:
Контрольные вопросы.
1. Что такое модуль Юнга? 2. Что такое абсолютное и относительное удлинение образца? 3. Что такое механическое напряжение? 4. Что такое коэффициент Пуассона? 5. Что такое абсолютное и относительное поперечное сжатие? 6. Какие из перечисленных характеристик относятся к материалу? 7. Какие из перечисленных характеристик относятся к образцу? 8. Закон Гука и его физический смысл. 9. Кривая зависимости s (e) и ее характерные точки и участки. 10. Деформация сдвига, иллюстрация пластических деформаций. 11. В чем состоит суть данного метода измерения Е? 12. Зависит ли модуль Юнга от нагрузки и стрелы прогиба? 13. Чем отличается деформация прогиба от деформации растяжения? 14. Напишите формулу для модуля Юнга по прогибу. Используемая литература [1] §14; [7] §21; [4] §48.
Лабораторная работа 1-17 “Изучение упругой деформации растяжения”
Цель работы: определить коэффициент упругости, модуль Юнга и коэффициент Пуассона для образца резины и проверить применимость для этого образца закона Гука.
Теоретическое введение
Жидкости сопротивляются изменению их объема, но не сопротивляются изменению формы. С этим свойством связан характерный для жидкостей закон Паскаля: передаваемое жидкостью во все стороны давление одинаково. Твердые же тела сопротивляются как изменению объема, так и изменению формы; они сопротивляются, как говорят, любому деформированию. Для твердых тел не справедлив закон Паскаля. Передаваемое твердым телом давление различно в разных направлениях. Давления, возникающие в твердом теле при его деформировании, называются напряжениями. В отличие от давления в жидкости, упругие напряжения в твердом теле могут иметь любые направления по отношению к площадке, на которую действуют силы. Но при всем разнообразии деформации твердых тел оказывается возможным любую деформацию тела свести к двум основным типам, которые поэтому называют элементарными деформациями. Ими являются растяжение (сжатие) и сдвиг. Так что, введя физические величины, характеризующие деформацию растяжения и сдвига, можно затем с помощью этих же величин характеризовать и другие типы деформаций (изгиб, кручение, …).
называют относительным удлинением (деформацией). При растяжении Отношение силы Опыт показывает, что при малых деформациях, при малых относительных удлинениях
где Если деформации тела достаточны малы, то по прекращению действия вызвавших деформацию внешних сил Соотношение (17.2) называют законом Гука. Модуль Юнга, однако, еще не характеризует полностью упругие свойства тела. Это видно и из рисунка 17.1. – продольное растяжение цилиндра связано с сокращением его поперечных размеров: удлиняясь, цилиндр одновременно становится более тонким. Характеристикой этого изменения является относительное поперечное сжатие
где | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 Пусть два слоя (рис.15.1) площади
Пусть два слоя (рис.15.1) площади  , отстоящих друг от друга на расстояние
, отстоящих друг от друга на расстояние 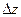 , движутся со скоростями v1 и v2 соответственно, Δv=v2–v1. Направление, в котором отсчитывается расстояние между слоями (ось z), перпендикулярно вектору скорости движения слоев. Величина
, движутся со скоростями v1 и v2 соответственно, Δv=v2–v1. Направление, в котором отсчитывается расстояние между слоями (ось z), перпендикулярно вектору скорости движения слоев. Величина ,
, , действующей между слоями, пропорциональна площади соприкосновения движущихся слоёв и градиенту скорости (закон Ньютона):
, действующей между слоями, пропорциональна площади соприкосновения движущихся слоёв и градиенту скорости (закон Ньютона): , (15.1)
, (15.1) – коэффициент вязкости (динамическая вязкость). Знак «–» показывает, что сила направлена противоположно градиенту скорости, то есть что быстрый слой тормозится, а медленный – ускоряется.
– коэффициент вязкости (динамическая вязкость). Знак «–» показывает, что сила направлена противоположно градиенту скорости, то есть что быстрый слой тормозится, а медленный – ускоряется. :
: . (15.2)
. (15.2) , (15.3)
, (15.3) где А – множитель, который зависит от расстояния между соседними положениями равновесия молекул в жидкости и от частоты колебаний молекул, Δ Е – энергия, которую надо сообщить молекуле жидкости, чтобы она могла перескочить из одного положения равновесия в другое, соседнее (энергия активации). Величина Δ Е обычно имеет порядок (2÷3).10-20 Дж, поэтому, согласно формуле (15.3), при нагревании жидкости на 100С вязкость её уменьшается на 20÷30%.
где А – множитель, который зависит от расстояния между соседними положениями равновесия молекул в жидкости и от частоты колебаний молекул, Δ Е – энергия, которую надо сообщить молекуле жидкости, чтобы она могла перескочить из одного положения равновесия в другое, соседнее (энергия активации). Величина Δ Е обычно имеет порядок (2÷3).10-20 Дж, поэтому, согласно формуле (15.3), при нагревании жидкости на 100С вязкость её уменьшается на 20÷30%. , перенесенного из одного слоя газа или жидкости в другой слой за время Δ t, можно найти из второго закона Ньютона:
, перенесенного из одного слоя газа или жидкости в другой слой за время Δ t, можно найти из второго закона Ньютона: . (15.4)
. (15.4) . (15.5)
. (15.5) . Теоретический расчет внутреннего трения для движения шарикав вязкой среде с небольшой скоростью, когда нет вихрей, приводит к формуле Стокса:
. Теоретический расчет внутреннего трения для движения шарикав вязкой среде с небольшой скоростью, когда нет вихрей, приводит к формуле Стокса: , (15.6)
, (15.6)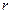 – радиус шарика,
– радиус шарика,  – скорость его движения,
– скорость его движения,  .
. , (15.7)
, (15.7) – масса шарика;
– масса шарика;  – плотность шарика;
– плотность шарика;  – ускорение свободного падения;
– ускорение свободного падения;  – объем шарика, равный:
– объем шарика, равный: ; (15.8)
; (15.8) – плотность жидкости.
– плотность жидкости.
 ,
,  :
:
 . (15.12)
. (15.12) . (15.13)
. (15.13) и время падения
и время падения  :
:  :
:
 . (15.14)
. (15.14) . (15.15)
. (15.15) – диаметр цилиндрического сосуда установки.
– диаметр цилиндрического сосуда установки. .
. , (15.16)
, (15.16) и доверительной вероятности α=0.95 равен: tn, α=2.57; Δηi=|ηср.– ηi|.
и доверительной вероятности α=0.95 равен: tn, α=2.57; Δηi=|ηср.– ηi|. , (15.17)
, (15.17) ,
, 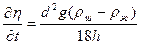 ,
,  .
. ,
,  и
и  нужно взять приборные погрешности.
нужно взять приборные погрешности. a= (ρ ш– ρ ж)
a= (ρ ш– ρ ж)  ,
, :
: . (15.18)
. (15.18)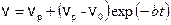 , (15.19)
, (15.19) . (15.20)
. (15.20) . (15.21)
. (15.21) <<1.
<<1. . Таким образом, оценим l 0, проинтегрировав (15.19) по времени на промежутке [0: t 1], где
. Таким образом, оценим l 0, проинтегрировав (15.19) по времени на промежутке [0: t 1], где  :
: ;
; и подстановки
и подстановки  ,
, ,
, . (15.22)
. (15.22) . Под воздействием внешних сил твердые тела в той или иной степени деформируются, то есть изменяют свою форму и объем. При всем разнообразии деформаций тел возможно любую деформацию свести к двум основным (элементарным): растяжению (сжатию) и сдвигу. Деформация растяжения характеризуется величиной относительного удлинения
. Под воздействием внешних сил твердые тела в той или иной степени деформируются, то есть изменяют свою форму и объем. При всем разнообразии деформаций тел возможно любую деформацию свести к двум основным (элементарным): растяжению (сжатию) и сдвигу. Деформация растяжения характеризуется величиной относительного удлинения  :
: , (16.1)
, (16.1)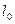 – длина тела до растяжения;
– длина тела до растяжения;  – после растяжения;
– после растяжения; 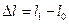 – абсолютное удлинение.
– абсолютное удлинение. .
. , (16.2)
, (16.2)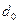 – поперечный размер тела до деформации, а
– поперечный размер тела до деформации, а  – после деформации..
– после деформации.. . Отношение
. Отношение (16.3)
(16.3)
 в механике деформируемых твердых тел называется напряжением и измеряется в Н/м2. Диаграмма растяжения схематически представлена на рис.16.1 в виде зависимости
в механике деформируемых твердых тел называется напряжением и измеряется в Н/м2. Диаграмма растяжения схематически представлена на рис.16.1 в виде зависимости  . Как видно из рис.16.1, при малых деформациях
. Как видно из рис.16.1, при малых деформациях 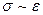 (напряжение пропорционально деформациям). Это есть известный из школы закон Гука. Точка А соответствует максимальному напряжению, при котором еще сохраняется пропорциональность между
(напряжение пропорционально деформациям). Это есть известный из школы закон Гука. Точка А соответствует максимальному напряжению, при котором еще сохраняется пропорциональность между  , (16.5)
, (16.5) – модуль упругости (модуль Юнга для данного материала).
– модуль упругости (модуль Юнга для данного материала). . Выше т.А удлинение
. Выше т.А удлинение  . Точного определения предела упругости тела дать вообще невозможно, так как малые остаточные деформации наблюдаются всегда.
. Точного определения предела упругости тела дать вообще невозможно, так как малые остаточные деформации наблюдаются всегда.
 , (16.6)
, (16.6) – сила, параллельная поверхности твердого тела, которая вызывает сдвиг.
– сила, параллельная поверхности твердого тела, которая вызывает сдвиг. , (16.7)
, (16.7) – коэффициент пропорциональности между напряжением сдвига
– коэффициент пропорциональности между напряжением сдвига  . В изотропных твердых телах (у таких тел свойства одинаковы во всех направлениях) эти три константы
. В изотропных твердых телах (у таких тел свойства одинаковы во всех направлениях) эти три константы  (16.8)
(16.8)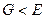 в твердых телах.
в твердых телах.
 , (16.9)
, (16.9) ;
; – длина образца между опорами;
– длина образца между опорами;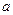 – ширина образца;
– ширина образца; – толщина образца.
– толщина образца.
 , где
, где
 В данной работе изучаются величины, характеризующие упругую деформацию растяжения. Пусть на цилиндр первоначальной длины
В данной работе изучаются величины, характеризующие упругую деформацию растяжения. Пусть на цилиндр первоначальной длины 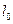 и диаметра
и диаметра  (рис. 17.1). При этом образец увеличивает свою длину на
(рис. 17.1). При этом образец увеличивает свою длину на  ,
,  – абсолютное удлинение.Величину
– абсолютное удлинение.Величину (17.1)
(17.1) , при сжатии
, при сжатии  . При однородном растяжении величина
. При однородном растяжении величина  на которое она действует, называется напряжением
на которое она действует, называется напряжением  , (17.2)
, (17.2) (17.3)
(17.3) – абсолютное поперечное сжатие. При растяжении
– абсолютное поперечное сжатие. При растяжении 


