Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод графической обработки результатов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из (18.27) и (18.29) получаем:
Таким образом, зависимость l = f (m) линейна и график её представляет собой прямую, тангенс угла наклона которой γ к оси абсцисс (m) равен коэффициенту при m: tgγ= g / k, или k = g ctg γ. (18.33) Для графической обработки результатов: 11. Построить график зависимости l = f (m). При большом разбросе экспериментальных точек нужно провести прямую линию так, чтобы сверху и снизу графика было одинаковое число точек. 12. Определить котангенс угла наклона γ графика к оси m. 13. Вычислить жесткость по формуле (18.33), результаты записать в табл.18.1. 14. Сравнить значение, полученное по формуле (18.33), с
Таблица 18.1.
Упражнение 2. Определение периода свободных затухающих колебаний. Измерения 1. Положить на подвеску груз массой m груза =0.5÷0.7 кг. Записать в табл.18.2 суммарную массу подвески и дополнительного груза m = m подвески+ m груза. 2. Зафиксировать и записать в табл.18.2 величину l 0 – положение равновесия нагруженного маятника. 3. Задать величину 4. Приготовить секундомер к работе, оттянуть маятник вниз до положения l нач. Отпустить маятник вместе с пуском секундомера и отсчитать N=100 полных колебаний (считать число полных колебаний по моментам возвращения маятника в нижнее положение максимального отклонения). 5. При счете «100» ОДНОВРЕМЕННО провести отсчет l – положения шкалы, до которого опустится груз и t – времени ста полных колебаний, НЕ ОСТАНАВЛИВАЯ СЕКУНДОМЕР и не прекращая отсчета числа колебаний. (Если одновременные измерения времени и амплитуды затруднительны, провести две серии опытов: одна – только для измерения времени, вторая – только амплитуды.) 6. Продолжить наблюдения и произвести те же измерения l и t для числа колебаний N=200,…700. Все результаты записать в таблицу 18.2. Обработка результатов измерений. 1. Вычислить амплитуду колебаний на N-ном (N=100,…700) колебании: 2. Вычислить период колебаний: 3. Найти средний период и его погрешность по формулам:
где Δ T i=| T i– T ср.|, 4. Вычислить циклическую частоту: 5. Вычислить коэффициент затухания по формуле (18.24): 6. Вычислить логарифмический декремент затухания λ:
и его погрешность. Примечание: погрешности Δω, Δβ и Δλ рассчитать по стандартным формулам для расчета погрешностей при косвенных измерениях. Например,
где 7. Вычислить теоретическую величину периода колебаний и сравнить с экспериментальным средним значением. 8. Записать кинематическое уравнение свободных (затухающих) колебаний для исследуемого пружинного маятника. Для этого в уравнение (18.18) подставить соответствующие числовые значения
Таблица 18.2.
Таблица 18.3.
Контрольные вопросы.
1. Что называют свободными или собственными колебаниями? 2. Какие колебания называются гармоническими? Дайте определение периода колебаний, частоты. Получите выражения для скорости и ускорения при механических гармонических колебаниях. 3. Сформулируйте закон Гука и укажите область его применимости. 4. Что такое жесткость пружины? От чего она зависит? 5. Выведите дифференциальное уравнение гармонических колебаний пружинного маятника и запишите его решение. 6. То же для затухающих колебаний; доказать формулы (18.18) и (18.19). Нарисуйте зависимость x(t) для затухающих колебаний. 7. Как изменятся амплитуда и период затухающих колебаний по сравнению с незатухающими гармоническими колебаниями? 8. Что такое коэффициент затухания? Запишите уравнение, выражающее закон убывания амплитуды затухающих колебаний, нарисуйте зависимость A(t). 9. Дайте определение логарифмического декремента затухания, докажите формулу (18.34). 10. Что такое добротность? Как она связана с уменьшением энергии колебаний? Используя (18.26), докажите (18.25) при условии малости затухания (β << ω0).
Используемая литература.
[5] §19.1, 19.2, 19.6; [3] §27.1, 27.2, 28.1; [1] §52-54; 58. [6] §3.3; 3.6, 3.7, 3.
Лабораторная работа 1-19 “Изучение колебаний физического маятника”
Цель работы: изучение зависимости периода колебаний от параметров маятников и измерение ускорения свободного падения. Теоретическое введение
Колебательным движением называется процесс, при котором система, многократно отклоняясь от положения равновесия, каждый раз вновь возвращается к нему. Существует общность закономерностей большого разнообразия колебательных процессов, поэтому все они могут быть сведены к совокупности простейших колебаний – гармонических. Гармоническим колебательным движением называется такое колебательное движение, при котором колеблющаяся величина изменяется с течением времени по закону синуса или косинуса. Основные характеристики колебательных процессов можно рассмотреть на примере механических колебаний материальной точки.
где ν – частота колебаний (число полных колебаний в единицу времени, Скорость
Продифференцировав (19.3), получим ускорение а:
Учитывая (19.1), будем иметь:
Выражение (19.5) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Его решением является гармоническая функция (19.1). Если вторая производная по времени какой-либо физической величины (не обязательно смещения!) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.
Направления вращающего момента M=– mgl.sinj. (19.6) По второму закону Ньютона для вращательного движения маятника:
где Из уравнений (19.6) и (19.7) имеем:
или
При малых углах
Сравнивая (19.9) и (19.5), устанавливаем, что j изменяется по гармоническому закону с круговой частотой ω, причем
а период колебаний маятника
Если вся масса маятника сосредоточена в одной точке (например, шарик, подвешенный на невесомой нерастяжимой нити), то такой маятник называют математическим (рис.19.3). В других случаях маятник называют физическим.
Для математического маятника момент инерции рассчитывается как для материальной точки:
I C= Тогда из (19.14) и (19.15) получаем: I O= где
и окончательно:
Для стержня по теореме Штейнера получим:
где L – длина стержня, m – его масса.
Точка О1, лежащая на прямой ОС на расстоянии l пр.от точки подвеса маятника (рис.19.5), называется центром качания маятника. Центр качания О1 и точка подвеса О обладают свойством взаимности: если маятник подвесить так, чтобы его ось качания проходила через точку О1, то точка О будет совпадать с новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними. Покажем это. По теореме Штейнера момент инерции I 1 маятника относительно оси, проходящей через точку О1, равен:
Из (19.18) и (19.20) вычислим IC: I C= I 1 – ml 12= I – ml 2. (19.21) Из (19.12) выразим момент инерции маятника
Далее после преобразований:
и после сокращения на (l1–l):
Но по определению приведенной длины физического маятника (19.12):
то есть l пр. = l 1+ l, что и требовалось показать. Для физического маятника – стержня из (19.12), (19.18) и (19.19) получим:
или:
Экспериментальная часть
1. Математический маятник. Примечание: выполнять только по заданию преподавателя.
Цель: определение ускорения свободного падения.
Оборудование: секундомер, математический маятник (шарик на нити на штативе).
1. Ознакомиться с установкой. Определить длину математического маятника l. Отвести маятник от положения равновесия на небольшой угол (10÷150) и отпустить. Пропустив 2-3 колебания, включить секундомер и определить время t, за которое совершится N полных колебаний (взять 50÷100 колебаний). Вычислить период колебаний маятника по формуле (19.23):
2. Повторить опыт (можно установить другую длину маятника) не менее 3 раз. Вычислить значение ускорения свободного падения по формуле:
3. Рассчитать погрешности измерений. 4. Все результаты занести в таблицу по форме 19.1.
Таблица 19.1.
Примечание: Среднее значение периода Тср. рассчитывается только в том случае, если длина маятника одна и та же во всех опытах. Ускорение свободного падения g рассчитать один раз, исходя из среднего значения периода. В этом случае погрешность периода рассчитывается по стандартной методике расчета погрешностей случайной величины:
где n – число опытов, ΔTi=|Ti–Tср.| – абсолютная погрешность каждого опыта, tn,α – коэффициент Стьюдента для доверительной вероятности α=0.95 Далее погрешность Δg рассчитать по стандартной формуле для расчета погрешностей при косвенных измерениях:
Если длина маятника в опытах была неодинаковой, ускорение свободного падения g рассчитывается в каждом опыте, затем усредняется, и его погрешность рассчитывается как при прямых измерениях случайной величины, то есть по формуле, аналогичной (19.25):
2, а) Физический маятник – кольцо (обруч).
Цель: определение ускорения свободного падения.
Оборудование: секундомер, физический маятник (кольцо или обруч на штативе с опорной призмой), линейка, штангенциркуль.
1. Измерить внешний D и внутренний диаметр d диска. 2. Определить при помощи секундомера время t, за которое совершится N полных колебаний (30-50). Вычислить период колебаний по формуле (19.23). 3. Повторить опыт не менее 3 раз (оптимально – 5). 4. Определить ускорение свободного падения по формуле (19.17), подставив в неё среднее значение периода колебаний. 5. Подсчитать погрешность измерений:
где производные
получены из (19.17). 6. Все результаты измерений и вычислений занести в таблицу по форме 19.2.
Форма 19.2.
2, б) Физический маятник – стержень.
Цель: определение приведенной длины физического маятника.
Оборудование: секундомер, физический маятник (стержень с опорной призмой), штатив, линейка. 1. Измерить длину стержня L. 2. Измерить l – расстояние от точки подвеса стержня до его центра. 3. Определить при помощи секундомера время t, за которое совершится N полных колебаний (30÷50). Вычислить период колебаний по формуле (19.23). 4. Повторить опыт 5 раз. 5. Рассчитать погрешность периода по формуле (19.25). 6. Определить экспериментальное значение приведенной длины физического маятника, исходя из формулы (19.12) и подставив в нее среднее значение периода колебаний:
7. Рассчитать погрешность приведенной длины:
8. Найти точку качания физического маятника: вычислить l 1= l пр – l, закрепить опорную призму маятника на расстоянии l 1 от центра стержня. 9. Повторить измерения времени t 1 для N колебаний и расчеты периода T 1 и его погрешности (пункты 3-5). Результаты записать в таблицу по форме 19.3.
Форма 19.3.
10. Сравнить T 1 и T, сделать выводы. 11. По формуле (19.22) определить l пр.теор. – теоретическое значение приведенной длины, рассчитать погрешность:
где производные рассчитываются, исходя из (19.22):
12. Все полученные данные записать в табл.19.3. 13. Сравнить теоретическое и экспериментальное значения l пр, сделать выводы.
Контрольные вопросы
1. Дайте определение колебательного процесса. 2. Какие колебания называются гармоническими? 3. Выведите дифференциальное уравнение гармонических колебаний. 4. Что называется математическим маятником? 5. Дайте определение физического маятника. 6. Что называется угловым ускорением? 7. Дайте определение момента инерции твердого тела. 8. Что такое момент силы? 9. Сформулируйте основной закон динамики вращательного движения. 10. Получите дифференциальное уравнение колебаний физического маятника. 11. Получите формулу для круговой частоты и периода колебаний физического маятника. 12. Сформулируйте теорему Штейнера. Как в данной работе она используется? 13. Что такое приведенная длина физического маятника? 14. Как найти период и частоту колебаний математического маятника? 15. Выведите формулу (19.17). 16. Что такое точка качания? Чем она замечательна?
Используемая литература
[5] §2.8, 7.1, 7.3, 19.1, 19.2; [3] §4.1, 4.2, 4.3, 27.1, 27.2; [1] §38, 39, 49, 50, 53, 54; [6] §3.3; 3.6, 3.7, 3.8; [7] §16, 18, 140, 141, 142.
Лабораторная работа 1-20 “Определение коэффициента трения качения методом исследования колебаний наклонного маятника”
Цель работы: Определение коэффициента трения качения методом исследования колебаний наклонного маятника.
Теоретическое введение
На любое движущееся тело действуют силы трения. Природа этих сил может быть различной, но в результате их действия всегда происходит превращение механической энергии во внутреннюю энергию трущихся тел, т. е. энергию теплового движения частиц. В механике различают два вида трения: сухое, или внешнее, между твердыми телами и внутреннее, или вязкое, между слоями жидкости или газа. Внешним трением называется явление возникновения в месте контакта двух соприкасающихся твердых тел касательных сил, препятствующих относительному перемещению этих тел. Внешнее трение между движущимися друг относительно друга телами называется кинематическим. Внешнее трение между взаимно неподвижными телами называется трением покоя. Оно проявляется в том, что для возникновения относительного перемещения двух соприкасающихся тел к одному из них нужно приложить внешнюю силу В зависимости от характера относительного движения различают трение скольжения, возникающее при поступательном перемещении (скольжении) одного тела по поверхности другого, и трение качения, возникающее тогда, когда одно тело катится по поверхности другого. Сила трения скольжения, возникающая при скольжении сухих поверхностей тел друг относительно друга, в основном вызывается механическим зацеплением между неровностями поверхностей и сцеплением между молекулами в областях их непосредственного соприкосновения. В приближенных расчетах можно считать, что величина силы трения скольжения пропорциональна силе нормального давления
где Коэффициент трения зависит также от множества других факторов: качества обработки трущихся поверхностей, наличия на них загрязнений, скорости скольжения и т. д. При качении тела вращения (шара, цилиндра, диска и т. д.) по плоской поверхности тело и поверхность в области соприкосновения деформируются. Поэтому линия действия силы реакции поверхности
Рис.20.1
Нормальная к плоскости составляющая
где Коэффициент трения качения имеет размерность длины и зависит от материала тел, состояния их поверхностей и ряда других факторов. Трение качения значительно меньше трения скольжения, поэтому повсюду, где возможно, трение скольжения колеса заменяют трением качения (использование шариковых и роликовых подшипников и т. д.).
Методика измерения
Одним из экспериментальных методов определения коэффициента трения качения является метод наблюдения колебаний наклонного маятника. При колебаниях маятника шарик катится по исследуемому образцу, при этом возникает сила трения качения, вызывающая затухание колебаний маятника. Нить маятника и образец наклонены относительно вертикали на одинаковый угол. Шарик движется под действием следующих сил: силы тяжести На рис.20.2 схематически изображен вид наклонного маятника сбоку, Силу тяжести
Сила
Рис. 20.2 На рис.20.3 изображена плоскость колебаний маятника. При отклонении маятника на небольшой угол
Сила трения качения, возникающая при движении шарика, направлена противоположно Пусть в некоторый момент времени шарик отклоняется на максимальный угол
где Тогда полная энергия
Подставляя в (20.7) выражения (20.5) и (20.4), получим
Рис.20.3 Действие силы трения качения вызывает уменьшение энергии колебаний. Полагая, что за период ам
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.104.103 (0.01 с.) |

 . (18.32)
. (18.32) .
. – начальную амплитуду (А 0=0.04÷0.10 м). Это определит величину
– начальную амплитуду (А 0=0.04÷0.10 м). Это определит величину  – начальную отметку на шкале, от которой оттянутый вниз от положения равновесия маятник начнет свободные колебания.
– начальную отметку на шкале, от которой оттянутый вниз от положения равновесия маятник начнет свободные колебания. .
. для
для  .
. ,
, ,
, – коэффициент Стьюдента для доверительной вероятности α=0.95.
– коэффициент Стьюдента для доверительной вероятности α=0.95. и ее погрешность
и ее погрешность  .
.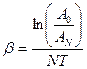 и его погрешность
и его погрешность  .
. , (18.34)
, (18.34) ,
, и
и 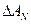 – погрешности амплитуды колебаний – принять равными 1 мм;
– погрешности амплитуды колебаний – принять равными 1 мм;  ;
;  ;
; 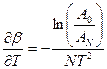 .
.
 ,
,  из табл.18.2 и 18.3. Сделать выводы.
из табл.18.2 и 18.3. Сделать выводы.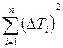

 , (19.1)
, (19.1) где А – амплитуда колебаний (абсолютное значение максимального смещения),
где А – амплитуда колебаний (абсолютное значение максимального смещения),  – фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, α0 – начальная фаза,
– фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, α0 – начальная фаза, 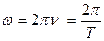 , (19.2)
, (19.2) , здесь
, здесь  – число колебаний за время t),
– число колебаний за время t), 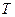 – период колебаний (время совершения одного полного колебания). Выражение (19.1) – кинематическое уравнение гармонического колебательного движения.
– период колебаний (время совершения одного полного колебания). Выражение (19.1) – кинематическое уравнение гармонического колебательного движения. колеблющейся материальной точки получим, продифференцировав (19.1) по времени:
колеблющейся материальной точки получим, продифференцировав (19.1) по времени: . (19.3)
. (19.3) . (19.4)
. (19.4) , или:
, или: . (19.5)
. (19.5)
 Любое тело (рис. 19.2), подвешенное в поле силы тяжести так, что точка подвеса О не совпадает с центром тяжести С, называется физическим маятником. Пусть отклонение маятника от положения равновесия характеризуется углом φ. При отклонении маятника от положения равновесия возникает вращающий момент силы
Любое тело (рис. 19.2), подвешенное в поле силы тяжести так, что точка подвеса О не совпадает с центром тяжести С, называется физическим маятником. Пусть отклонение маятника от положения равновесия характеризуется углом φ. При отклонении маятника от положения равновесия возникает вращающий момент силы  , стремящийся вернуть маятник в положение равновесия. Его величина М=mgl. sin j, где m – масса маятника; l – расстояние от центра тяжести маятника до точки подвеса, d=l .sin j – плечо силы тяжести (кратчайшее расстояние от линии действия силы до оси вращения).
, стремящийся вернуть маятник в положение равновесия. Его величина М=mgl. sin j, где m – масса маятника; l – расстояние от центра тяжести маятника до точки подвеса, d=l .sin j – плечо силы тяжести (кратчайшее расстояние от линии действия силы до оси вращения). противоположны (момент силы возвращает маятник к положению равновесия), поэтому
противоположны (момент силы возвращает маятник к положению равновесия), поэтому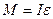 , (19.7)
, (19.7) – момент инерции маятника относительно оси, проходящей через точку подвеса; e – угловое ускорение маятника, равное второй производной угла поворота:
– момент инерции маятника относительно оси, проходящей через точку подвеса; e – угловое ускорение маятника, равное второй производной угла поворота: 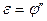 .
. ,
, . (19.8)
. (19.8) , и уравнение (19.8) будет иметь вид:
, и уравнение (19.8) будет иметь вид: . (19.9)
. (19.9) , (19.10)
, (19.10)
 . (19.11)
. (19.11) Приведенной длиной физического маятника называется длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник:
Приведенной длиной физического маятника называется длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник: . (19.12)
. (19.12)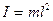 , поэтому период его колебаний равен:
, поэтому период его колебаний равен: . (19.13)
. (19.13) В лабораторной работе используется физический маятник в виде кольца (рис.19.4) или в виде однородного тонкого стержня (рис.19.5). Момент инерции маятника относительно точки подвеса О можно найти по теореме Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно данной оси, и произведения массы тела на квадрат расстояния между осями. Для кольца получим:
В лабораторной работе используется физический маятник в виде кольца (рис.19.4) или в виде однородного тонкого стержня (рис.19.5). Момент инерции маятника относительно точки подвеса О можно найти по теореме Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно данной оси, и произведения массы тела на квадрат расстояния между осями. Для кольца получим: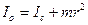 . (19.14)
. (19.14) Здесь
Здесь 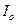 – момент инерции маятника относительно оси, проходящей через точку подвеса O, I C – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен:
– момент инерции маятника относительно оси, проходящей через точку подвеса O, I C – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен: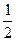 m (R 2+ r 2), (19.15)
m (R 2+ r 2), (19.15)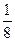 m (D 2+3 d 2), (19.16)
m (D 2+3 d 2), (19.16) и
и  – внешний и внутренний диаметры диска соответственно. Из формулы (19.11) выразим ускорение свободного падения с учетом, что l=r=d/2, и из (19.16) подставим момент инерции:
– внешний и внутренний диаметры диска соответственно. Из формулы (19.11) выразим ускорение свободного падения с учетом, что l=r=d/2, и из (19.16) подставим момент инерции: ,
,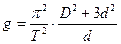 . (19.17)
. (19.17)
 , (19.18)
, (19.18) , (19.19)
, (19.19) Можно показать, что для любого маятника приведенная длина lпр. больше, чем расстояние l от центра масс до точки подвеса (длины физического маятника): из (19.12) и (19.18) следует, что
Можно показать, что для любого маятника приведенная длина lпр. больше, чем расстояние l от центра масс до точки подвеса (длины физического маятника): из (19.12) и (19.18) следует, что .
. . (19.20)
. (19.20) и запишем аналогичную формулу для I 1:
и запишем аналогичную формулу для I 1: 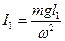 . Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О1, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (19.21) получим уравнение:
. Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О1, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (19.21) получим уравнение: .
. ,
, .
.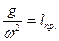 ,
, ,
, . (19.22)
. (19.22) . (19.24)
. (19.24) , (19.25)
, (19.25) , (19.26)
, (19.26) .
. ,
,
 ,
, 
 ,
, 

 . (19.25)
. (19.25)
 ,
, ;
; 
 .
. , где
, где  - так называемая предельная сила трения покоя.
- так называемая предельная сила трения покоя.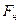 , а следовательно, и силе реакции опоры
, а следовательно, и силе реакции опоры  (20.1)
(20.1) - безразмерный коэффициент трения скольжения, зависящий от свойств материалов обоих тел.
- безразмерный коэффициент трения скольжения, зависящий от свойств материалов обоих тел. не совпадает с линией действия силы нормального давления
не совпадает с линией действия силы нормального давления 
 численно равна силе нормального давления, а горизонтальная составляющая представляет собой силу трения качения
численно равна силе нормального давления, а горизонтальная составляющая представляет собой силу трения качения  . В первом приближении можно считать, что
. В первом приближении можно считать, что (20.2)
(20.2)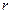 - радиус катящегося тела;
- радиус катящегося тела;  - коэффициент трения качения.
- коэффициент трения качения. , силы натяжения нити
, силы натяжения нити  - стремится вернуть маятник в положение равновесия.
- стремится вернуть маятник в положение равновесия. . Составляющая
. Составляющая  (20.3)
(20.3) (20.4)
(20.4)
 от положения равновесия возникает возвращающая сила
от положения равновесия возникает возвращающая сила  (20.5)
(20.5) -го колебания
-го колебания  без учета трения равна работе по подъему шарика на угол
без учета трения равна работе по подъему шарика на угол 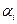 . Элементарная работа, совершаемая при отклонении шарика на малый угол
. Элементарная работа, совершаемая при отклонении шарика на малый угол  , равна
, равна (20.6)
(20.6)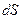 - дуга, которую описывает шарик при его отклонении на малый угол
- дуга, которую описывает шарик при его отклонении на малый угол  — расстояние от оси вращения до центра шарика.
— расстояние от оси вращения до центра шарика. (20.7)
(20.7) (20.8)
(20.8)