
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1-09 “Определение момента инерции маховика”.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: изучить применение закона сохранения энергии для вращательного движения; экспериментально определить момент инерции твердого тела.
Теоретическое введение
 В работе изучаются такие движения в механике, при которых существенна конечная протяженность тел – их нельзя рассматривать в данных условиях как материальные точки. Если тело является настолько жестким, что деформациями, возникающими при его движении можно пренебречь, то тело можно рассматривать как недеформируемое, абсолютно твердое (или просто твердое) тело. То есть такое, взаимное расположение частей которого остается неизменным во время движения. В работе изучаются такие движения в механике, при которых существенна конечная протяженность тел – их нельзя рассматривать в данных условиях как материальные точки. Если тело является настолько жестким, что деформациями, возникающими при его движении можно пренебречь, то тело можно рассматривать как недеформируемое, абсолютно твердое (или просто твердое) тело. То есть такое, взаимное расположение частей которого остается неизменным во время движения.
Простейшим движением твердого тела является поступательное. Тело перемещается параллельно самому себе; все точки его имеют одинаковую скорость и описывают траектории одинаковой формы, только смещенные по отношению друг к другу. При этом кинетическая энергия равна:
где Другим простейшим видом движения твердого тела является вращение тела вокруг оси. Определим кинетическую энергию твердого тела, закрепленного на неподвижной оси, вокруг которой оно может свободно вращаться (рис.9.1); точка О – след этой оси. К одной из точек тела А приложена внешняя сила
Величина Так что величины скоростей различных
Кинетическая энергия такого элемента по определению равна:
Просуммировав эти энергии, получим полную кинетическую энергию вращающегося твердого тела:
Стоящая здесь в скобках сумма зависит от того, с каким именно твердым телом мы имеем дело (от его формы, размеров и распределения массы в нем), а также от того, как расположена в нем ось вращения. Эта величина, характеризующая твердое тело и выбранную ось вращения, называется моментом инерции относительно данной оси и обозначается буквой
Если твердое тело – сплошное, то его нужно разделить на бесконечно большое количество бесконечно малых частей. Суммирование в (9.6) заменяем интегрированием.
Так как
Вычисление таких интегралов в общем случае представляет собой сложную задачу. Лишь для тел симметричной формы при однородном распределении массы по объему тела их моменты инерции определить достаточно просто, если ось вращения проходит через центр масс (шар, цилиндр, диск, стержень). Поэтому моменты инерции сложных тел проще определять экспериментально. Таким образом, кинетическая энергия вращающегося тела может быть записана в виде:
Это выражение формально похоже на выражение для энергии поступательного движения (9.1), отличаясь от него тем, что вместо скорости Далее кинетическую энергию произвольно движущегося твердого тела можно представить в виде суммы поступательной и вращательной энергий, если ось вращения проходит через центр инерции тела. Тогда для кинетической энергии произвольно движущегося тела имеем:
здесь первое слагаемое – кинетическая энергия поступательного движения, Независимо от характера движения тел (поступательного или вращательного) для замкнутых систем справедлив закон сохранения механической энергии (суммы кинетической и потенциальной энергий), если между телами действуют только консервативные силы. Если в замкнутой системе тел действуют и не консервативные силы, например, силы трения, то изменение механической энергии системы равно работе неконсервативных сил:
В данной лабораторной работе используется именно этот закон. Необходимо еще дать определение работы при вращении твердого тела. Выражение для работы
Методика измерений В основе метода лежит закон сохранения энергии:
где
Из уравнения (9.13) необходимо определить момент инерции маховика Величина
Так как груз движется равноускоренно, то скорость груза в конце движения будет равна
Угловая скорость маховика по определению:
Момент сил трения Изменение потенциальной энергии груза равно работе против момента сил трения:
где
Подставив в выражение (9.13) значения
Экспериментальная установка
Порядок выполнения работы
1. Наматывая шнур на шкив, поднять груз на высоту h1 (во всех опытах h1 одинаковая). 2. Освободив груз и включив секундомер, определить время падения t груза до нижней точки. 3. Определить высоту 4. Повторить все измерения 5 раз. 5. Все данные занести в таблицу 1. 6. Рассчитать по формуле (9.18) величину момента сил трения. Принять 7. Вычислить по формуле (9.19) момент инерции маховика. 8. Вычислить погрешность измерений. 9. По теоретической формуле рассчитать момент инерции вращающихся деталей установки.
Форма 9.1.
Контрольные вопросы
1. Что такое момент инерции твердого тела? 2. Сформулируйте основной закон динамики вращательного движения. 3. Сделайте подробный вывод формулы (9.19). 4. О каком законе сохранения идет речь в этой работе? Сформулируйте его. 5. Чему равна работа при вращении тела вокруг оси? 6. Дайте представление о моделях тел в механике и приведите примеры. 7. Представьте определение замкнутой системы тел. 8. Чем отличаются консервативные силы от неконсервативных? Приведите примеры.
Используемые литература
[1] §24, 38, 39, 41; [2] §24, 31-33; [3] §3.4; 4.1-4.3; [7] §16, 18; [6] §2.8; 7.1; 7.2.
Лабораторная работа 1-10 “Маятник Максвелла” Цель работы: применение основных законов динамики к изучению движения твёрдых тел, определение момента инерции маятника Максвелла. Теоретическое введение При применении основных законов динамики к изучению движения твердых тел необходимо исходить их того, что в общем случае движение твердого тела определяется двумя векторными уравнениями. Одно из них – уравнение движения центра тяжести твердого тела
где Другое – уравнение моментов в системе отсчета, жестко связанной с центром тяжести (в ней покоится центр тяжести)
где
Напомним, что для описания движения ось моментов выбираем жестко связанную с маятником и проходящую через его центр тяжести. Но такая система отсчета при ускоренном движении маятника будет неинерциальной. В ней будут действовать силы инерции и при составлении уравнения моментов (10.2) должны быть учтены в правой части уравнения моменты сил инерции. Однако, для плоского движения твердого тела можно выбрать ось, связанную с телом, относительно которой моменты сил инерции оказываются равными нулю, и поэтому уравнение моментов имеет такой же вид, как и для осей, неподвижных в пространстве. Этим свойством обладает ось, движущаяся поступательно (т.е. перпендикулярно к плоскостям, в которых движутся точки тела) и проходящая через центр тяжести тела. Тогда равнодействующая сил инерции, так же как и равнодействующая сил тяжести, будет приложена к центру тяжести тела и момент ее относительно оси, проходящей через центр тяжести, будет равен нулю. В нашем случае этой осью будет геометрическая ось диска. Так как эта ось неподвижна относительно диска, можно написать выражение момента импульса относительно этой оси
где а уравнение моментов
где Составим далее уравнения плоского движения диска. На диск массой
Так как центр тяжести опускается как раз на столько, на сколько раскручивается нить, то величина перемещения центра тяжести диска Дифференцируя это соотношение дважды по времени, найдем связь между ускорением центра масс и угловым ускорением диска:
Решая систему уравнений (10.5), (10.6) и (10.7), находим ускорение
и силу натяжения нити
Из формул (10.8),(10.9) следует, что ускорение и сила натяжения нити не зависят от того, в каком направлении движется маятник - вверх или вниз. Следовательно, вес движущегося маятника Из уравнения (10.8) находим момент инерции маятника:
Ускорение
Итак, момент инерции маятника:
Поскольку силы трения не принимаются во внимание, то формулу для момента инерции маховика можно получить также из закона сохранения механической энергии. Для двух крайних положений диска:
Отсюда
Экспериментальная часть Приборы и оборудование: маятникМаксвелла и принадлежности к нему (набор съёмных колец, штангенциркуль). Экспериментальная установка
Для наблюдения за движением маятника применяется установка, показанная на рис. 10.2. На вертикальной стойке (1) укреплены два кронштейна. На верхнем подвижном кронштейне (2) расположены электромагнит (3), фотоэлектрический датчик (4) и вороток (5), позволяющий регулировать длину нити подвеса маятника. Момент инерции маятника изменяют с помощью съёмных колец (6). В верхнем положении маятник с кольцом удерживается электромагнитом, время его движения между крайними точками измеряется секундомером. Порядок выполнения работы
1. С помощью регулируемых по высоте ножек установите стойку прибора в вертикальное положение и, регулируя воротком длину нити, добейтесь горизонтального положения оси маятника (при проведении опытов следите, чтобы положение оси оставалось горизонтальным). Включите в электрическую сеть вилку кабеля питания. Включите прибор в сеть, нажав кнопку “сеть” 2. На обод маховичка наденьте съёмное кольцо. Выпишите массы: 3. Измерьте высоту расположения нижней грани маятника с кольцом 4. Тщательно, виток к витку, наматывайте на стержень нити подвеса до достижения крайнего верхнего положения. Зафиксируйте положение маятника электромагнитом, кнопка “пуск” должна быть отжата. 5. Измерьте высоту расположения нижней грани маятника с кольцом 6. Измерьте диаметр оси маятника штангенциркулем, определите радиус оси 7. Одновременно с нажатием кнопки “пуск” (выкл. электромагнит) включить секундомер. Остановить отсчет времени по достижении маятником крайнего нижнего положения. Записать результат измерения в таблицу 10.1, повторить опыт с первым кольцом по п.п. 4-7 4-5 раз для накопления статистики. 8. Рассчитать среднее арифметическое значение 9. Вычислите по формуле (10.10) момент инерции маятника 10. Измерьте радиусы 11. Рассчитайте теоретическое значение
12. Сравните теоретическое и экспериментальное значение момента инерции маятника. 13. Поменяйте съемное кольцо на другое и выполните действия по пунктам 2-10. 14. Сделайте выводы по работе.
Форма 10.1
Расчёт погрешностей:
Контрольные вопросы: 1. Какие физические величины характеризуют поступательное движение твердого тела? Их определение, физический смысл, формулы, единицы измерения. 2. Какими величинами описывается вращение твёрдого тела вокруг закреплённой оси? Физический смысл этих величин, формулы 3. Из каких простых движений слагается плоское движение твёрдого тела? 4. Вывод формулы момента инерции маховика на основе закона сохранения энергии.
Используемая литература:
[3] §4.1; 4.2; 4.3; [6] §1.31; 1.32; 1.33; 1.34; [7] §16-19; [5] §7.1-7.3.
Лабораторная работа 1-11 “Изучение характеристик механического гироскопа”
Цель работы: ознакомиться с особенностями динамики быстровращающегося твердого тела и измерить его основные параметры: момент импульса, момент инерции и скорость прецессии.
Теоретическое введение
Гироскопические приборы и устройства находят широкое применение в различных отраслях техники. Элементарное представление об особенностях поведения гироскопа дает обыкновенный волчок с его поразительно малой восприимчивостью к воздействию внешних сил и моментов. Гироскопы чаще всего применяются для ориентации, для определения тех или иных направлений. Также гироскопы используются в горном деле для определения кривизны буровых скважин, для записи неправильностей железнодорожного пути. В авиации гироскопические приборы применяются в качестве основных чувствительных элементов (определение направления вертикали и курса), а также для измерения угловой скорости самолета. Гироскопом называют симметричное твердое тело, быстро вращающееся вокруг одной из осей симметрии. Ось может изменять свое положение в пространстве. В простейшем варианте гироскоп выполняется в виде массивного диска, насаженного на вал. (рис. 11.1) Гироскоп – слово греческого происхождения (гирос) – вращение (скопейн) – видеть, наблюдать. Это название прибору дал французский физик Леон Фуко. В общем случае под гироскопом понимают твердое тело любой формы, которое совершает вращательное движение. Земной шар, делающий один оборот за сутки, подчиняется гироскопическим законам точно так же, как технические гироскопы, вращающиеся с большой угловой скоростью относительно главной оси по сравнению со скоростями вокруг любых других осей. Гироскопами заполнен микромир: орбитальное движение и спины электронов, спин атомных ядер является неисчерпаемой кладовой гироскопии в недрах микромира. Гироскоп в кардановом подвесе имеет три степени свободы. Если центр масс гироскопа совпадает с точкой О – точкой опоры гироскопа, то гироскоп называется уравновешенным Движение гироскопа определяется уравнением моментов:
Дополнительное вращение оси гироскопа с угловой скоростью При вращении оси соответствующая угловая скорость При отсутствии внешнего вращающегося момента
вектор Нарушим равновесие гироскопа, сдвинув противовес на
т.е гироскоп за время
разделим обе части на
где поскольку
т.е. подставляя (11.5) в (11.1) получим
где
Экспериментальная часть Общий вид гироскопа представлен на рис. 11.1. где 1 – основание; 2 – колонка; 3 – кронштейн; 4 – фотоэлектрический датчик №1; 5 – внешняя втулка вращательного соединителя; 6 – фотоэлектрический датчик №2; 7 – электрический двигатель; 8 – кронштейн; 9 – ротор; 10 – защитный экран; 11 – рычаг; 12 – груз; 13 – диск; 14 – указатель; 15 – блок управления и измерения.
Методика измерений
Одна из точек гироскопа должна быть закреплена - это точка опоры гироскопа О.
Гироскоп в кардановом подвесе имеет три степени свободы. Если центр масс гироскопа совпадает с точкой О, то гироскоп называется уравновешенным (рис.11.2).
Ротор гироскопа при своем вращении увлекает близлежащие слои воздуха, в результате чего возникает сила вязкого трения, определяемая уравнением Ньютона:
где
интеграл берется по всей поверхности соприкосновения ротора с воздушными слоями. Как видно из рис. 11.2, при роторе цилиндрической формы радиуса R и толщиной h всю его поверхность можно разбить на боковую поверхность и две поверхности основания. Таким образом:
при этом на боковой поверхности На поверхности оснований На основании вышесказанного находим полный момент сил трения (момент сил на оси OY)
Ттаким образом, для коэффициента динамической вязкости получим:
где А – постоянный параметр гироскопа: R=(80±2) мм; a=(20±1) мм; b=(4±0,5)мм; h=(15±1)мм; Экспериментальная установка
Установка представляет собой собственно гироскоп и сопряженные с ним измерительные системы и имеет следующие технические и метрологические данные: диапазон управляемых оборотов двигателя 1000¸10000 об/мин; диапазон измеряемого времени процессии 1¸99999 мс; диапазон измеряемого угла процессии 10¸9900; масса перемещаемого груза 0,6±0,05 кг; погрешность измерения времени 0,02%; погрешность измерения скорости оборотов не больше 2,5%. Внешний вид гироскопа представлен на рисунке 11.1 на основании 1 оснащенном ножками с регулируемой высотой, позволяющим произвести выравнивание прибора, закреплена колонка 2. на колонке закреплен кронштейн 3, на котором закреплен фотоэлектрический датчик №1 (4) и внешняя втулка вращательного соединителя (5). Вращательный соединитель позволяет гироскопу обращаться вокруг вертикальной оси и обеспечивает питание электрическим током фотоэлектрического датчика №2 (6) и электрического двигателя (7) посредством разъемов. Электрический двигатель смонтирован на кронштейне (8) таким образом, что допускает вращения в вертикальной плоскости. На валу двигателя закреплен ротор (9), защищаемый экраном (10). Рычаг (11), закрепленный на корпусе двигателя, имеет нанесенную метрическую шкалу. На рычаге закреплен груз (12). При помощи перемещения груза по рычагу можно уравновесить гироскоп, перемещая центр масс системы. Поворот гироскопа вокруг вертикальной оси можно считывать с диска (5) с нанесенной угловой шкалой, при помощи указателя (14). Диск (5) имеет на окружности отверстия через каждые 50, которые, подсчитываемые фотоэлектрическим датчиком №1, передают в блок управления измерений (3), информацию об угле поворота гироскопа. Ротор (9) имеет на окружности прорези, которые, подсчитываемые фотоэлектрическим датчиком №2, передают в блок управления и измерений информацию о скорости оборотов электрического двигателя.
Порядок выполнения работы
Задание 1: Измерение скорости прецессии и кинетического момента гироскопа. 1. Сбалансируйте гироскоп относительно осей X, Y, Z. Это делается путем перемещения противовеса по стержню. Сбалансированный гироскоп должен находится в положении безразличного равновесия. 2. Запишите положение груза, при котором гироскоп сбалансирован (от этого положения отсчитывается величина 3. Нажмите кнопку " СЕТЬ ", выждите 2-3 минуты, чтобы вращение ротора стабилизировалось. 4. Регулятором задайте скорость вращения маховика 5. Вычислите значение угловой скорости: 6. Переместите груз по рычагу на 7. Нажмите кнопку " СБРОС ". 8. Отпустите гироскоп и после его поворота на угол 20о нажмите кнопку " СТОП ". 9. Определите по счетчикам угол поворота | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 (9.1)
(9.1) – скорость тела,
– скорость тела,  – его полная масса.
– его полная масса. . Мысленно разделим тело на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки.
. Мысленно разделим тело на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки.  – масса этого элемента,
– масса этого элемента,  – его расстояние до оси вращения. При вращении различные точки тела описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения. Если за время
– его расстояние до оси вращения. При вращении различные точки тела описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения. Если за время 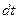 тело поворачивается на угол
тело поворачивается на угол 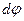 , то путь
, то путь  , проходимый за это время какой-либо точкой тела
, проходимый за это время какой-либо точкой тела  , будет равен
, будет равен  . Разделив
. Разделив  (9.2)
(9.2) одинакова для всех точек тела и представляет собой угловое перемещение тела за единицу времени. Она называется угловой скоростью тела
одинакова для всех точек тела и представляет собой угловое перемещение тела за единицу времени. Она называется угловой скоростью тела  .
. -х элементов равны:
-х элементов равны: (9.3)
(9.3)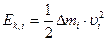 (9.4)
(9.4) (9.5)
(9.5)
 (9.6)
(9.6) . (9.7)
. (9.7) (
( – плотность тела), то вычисление момента инерции сводится к объемным интегралам:
– плотность тела), то вычисление момента инерции сводится к объемным интегралам: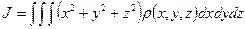 (9.8)
(9.8) (9.9)
(9.9) , (9.10)
, (9.10)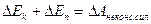 (9.11)
(9.11) при вращении твердого тела вокруг оси легко представить, если продолжить отмеченную аналогию между соотношениями динамики поступательного движения и динамики твердого тела: вместо линейной скорости
при вращении твердого тела вокруг оси легко представить, если продолжить отмеченную аналогию между соотношениями динамики поступательного движения и динамики твердого тела: вместо линейной скорости  , вместо пути
, вместо пути  – угол поворота
– угол поворота  . Тогда вместо соотношения
. Тогда вместо соотношения  , определяющего работу при поступательном движении, для вращательного движения имеем:
, определяющего работу при поступательном движении, для вращательного движения имеем: (9.12)
(9.12) (9.13)
(9.13) – потенциальная энергия груза в начальный момент;
– потенциальная энергия груза в начальный момент; – кинетическая энергия груза в нижней точке траектории;
– кинетическая энергия груза в нижней точке траектории;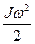 – кинетическая энергия маховика, когда груз находится в нижней точке траектории;
– кинетическая энергия маховика, когда груз находится в нижней точке траектории;  – работа по преодолению момента силы трения в подшипниках опоры маховика.
– работа по преодолению момента силы трения в подшипниках опоры маховика. – угол поворота маховика за время падения груза с высоты
– угол поворота маховика за время падения груза с высоты 
 . (9.14)
. (9.14) . (9.15)
. (9.15) . (9.16)
. (9.16) можно найти следующим образом. После того, как груз достигнет нижней точки, маховик, вращаясь по инерции, поднимет груз на новую высоту
можно найти следующим образом. После того, как груз достигнет нижней точки, маховик, вращаясь по инерции, поднимет груз на новую высоту  , которая меньше
, которая меньше  , (9.17)
, (9.17) – угол поворота маховика за время прохождения грузом пути
– угол поворота маховика за время прохождения грузом пути  . Отсюда момент силы трения в опорах равен:
. Отсюда момент силы трения в опорах равен: . (9.18)
. (9.18) ,
,  . (9.19)
. (9.19) Схема установки представлена на рис.9.2. Маховик 1 радиусом
Схема установки представлена на рис.9.2. Маховик 1 радиусом  имеет шкив 2 радиусом r. Необходимо определить момент инерции данной системы. На шкив намотана нить, к которой прикреплен груз 3 массой
имеет шкив 2 радиусом r. Необходимо определить момент инерции данной системы. На шкив намотана нить, к которой прикреплен груз 3 массой  над основанием отсчитывается по линейке 4, время опускания груза измеряется секундомером.
над основанием отсчитывается по линейке 4, время опускания груза измеряется секундомером.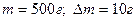 .
.
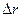





 , (10.1)
, (10.1) – скорость его центра тяжести;
– скорость его центра тяжести;  – сумма всех внешних сил, действующих на тело.
– сумма всех внешних сил, действующих на тело. , (10.2)
, (10.2) – момент импульса тела относительно оси, проходящей через центр тяжести, а
– момент импульса тела относительно оси, проходящей через центр тяжести, а  – суммарный момент всех внешних сил относительно этой оси.
– суммарный момент всех внешних сил относительно этой оси. Простейшее движение твердого тела – плоское движение. В этом случае каждая его точка движется, оставаясь в одной из параллельных друг другу плоскостей. Примером плоского движения является качение цилиндра по плоскости. Другим примером является маятник Максвелла, который представляет собой однородный круглый диск радиуса R, подвешенный на двух нерастяжимых нитях, намотанных на его горизонтальную ось (рис 10.1). Под действием силы тяжести диск опускается, и нити разматываются до полной длины. В нижнем положении раскрутившийся маховичок продолжает вращение в том же направлении и наматывает нить на ось. Дойдя до верхней точки, диск останавливается и снова начинает свое движение, совершая таким образом колебания по вертикальной прямой линии; поэтому такое устройство и называется маятником.
Простейшее движение твердого тела – плоское движение. В этом случае каждая его точка движется, оставаясь в одной из параллельных друг другу плоскостей. Примером плоского движения является качение цилиндра по плоскости. Другим примером является маятник Максвелла, который представляет собой однородный круглый диск радиуса R, подвешенный на двух нерастяжимых нитях, намотанных на его горизонтальную ось (рис 10.1). Под действием силы тяжести диск опускается, и нити разматываются до полной длины. В нижнем положении раскрутившийся маховичок продолжает вращение в том же направлении и наматывает нить на ось. Дойдя до верхней точки, диск останавливается и снова начинает свое движение, совершая таким образом колебания по вертикальной прямой линии; поэтому такое устройство и называется маятником. (10.3)
(10.3) – момент инерции диска относительно этой же оси,
– момент инерции диска относительно этой же оси,  – угловая скорость;
– угловая скорость; , (10.4)
, (10.4) – угловое ускорение диска.
– угловое ускорение диска. и натяжение нити
и натяжение нити 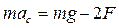 , (10.5)
, (10.5) . (10.6)
. (10.6) и угол поворота его
и угол поворота его 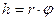 .
.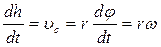 и
и  . (10.7)
. (10.7) (10.8)
(10.8)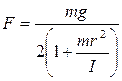 (10.9)
(10.9) не зависит от направления движения маховичка и оказывается меньше веса маятника в состоянии покоя. (Сравните движение маятника Максвелла с равноускоренным движением по вертикальной прямой линии груза, подвешенного на нити.)
не зависит от направления движения маховичка и оказывается меньше веса маятника в состоянии покоя. (Сравните движение маятника Максвелла с равноускоренным движением по вертикальной прямой линии груза, подвешенного на нити.)
 находится по измеренному времени движения
находится по измеренному времени движения  и пройденному пути:
и пройденному пути: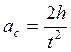 .
. . (10.10)
. (10.10)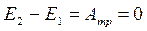 или
или  .
. .
.
 - масса оси,
- масса оси,  - масса маховичка,
- масса маховичка,  - масса съемного кольца, указанные непосредственно на них. Сумму масс
- масса съемного кольца, указанные непосредственно на них. Сумму масс  , выраженную в кг, занести в таблицу 10.1.
, выраженную в кг, занести в таблицу 10.1. . Запишите значение
. Запишите значение  и занесите его значение, выраженное в метрах, в таблицу по форме 10.1.
и занесите его значение, выраженное в метрах, в таблицу по форме 10.1. . Запишите значение в таблицу.
. Запишите значение в таблицу. . Проведите расчет погрешности измерения.
. Проведите расчет погрешности измерения. ,
, 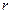 ,
,  ,
,  ; где
; где  момента инерции маятника.
момента инерции маятника.
 кг
кг






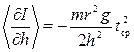
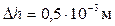

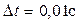

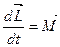 (11.1)
(11.1) – момент внешних сил.
– момент внешних сил. под действием постоянного момента сил
под действием постоянного момента сил 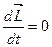 ,
,  (11.2)
(11.2) . Зададим вращающий момент
. Зададим вращающий момент 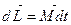 , (11.3)
, (11.3) . Считаем, что вектор
. Считаем, что вектор  (11.4)
(11.4) или
или 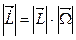 (11.5)
(11.5)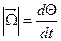 – скорость прецессии гироскопа
– скорость прецессии гироскопа
 (11.6)
(11.6)
 (11.7)
(11.7)

 ; (11.8)
; (11.8) – коэффициент внутреннего трения (или коэффициент динамической вязкости),
– коэффициент внутреннего трения (или коэффициент динамической вязкости),  – градиент скорости вдоль нормали к направлению движения,
– градиент скорости вдоль нормали к направлению движения, 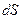 – площадь поверхности соприкосновения слоев. Момент этих сил сопротивления можно вычислить как:
– площадь поверхности соприкосновения слоев. Момент этих сил сопротивления можно вычислить как: ,
,
 , где а – расстояние от поверхности диска до кожуха:
, где а – расстояние от поверхности диска до кожуха: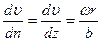 ,
,  , где
, где 
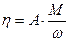
 ,
,
 см влево от положения равновесия, удерживая рычаг в исходном (горизонтальном) положении, задавая тем самым момент сил относительно оси OY.
см влево от положения равновесия, удерживая рычаг в исходном (горизонтальном) положении, задавая тем самым момент сил относительно оси OY. и время поворота
и время поворота 


