
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент импульса системы материальных точек. Уравнение моментовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Векторным произведением двух векторов а и b называется вектор с, модуль которого с связан с модулями сомножителей а и b и углом между ними a соотношением: c=a × b ×cosa.
Направление вектора с определяется следующим образом. Во–первых, с направлен перпендикулярно плоскости, в которой расположены а и b. Из двух возможных направлений выбирается то, куда перемещается буравчик (правый винт), вращающийся от направления первого сомножителя ко второму по кратчайшему направлению (см.рис.1). Обозначается векторное произведение а и b как [ а, b ] или a ´ b. Из определения векторного произведения видно, что оно обладает следующими очевидными свойствами: [ а, b ] = – [ b, а ] [ a, a ] = 0. Можно также доказать, что: [a а, b ] = [ а,a b ] = a[ а, b ], где a – скаляр, а также: [ а+b, c ] =[ а, c ]+ [ b, c ]. Иногда полезно иметь в виду, что величина векторного произведения двух векторов равна площади параллелограмма, двумя смежными сторонами которого являются эти векторы. Или иначе: величина векторного произведения двух векторов равна удвоенной площади треугольника, двумя сторонами которого являются эти векторы. 1. Моментом импульса материальной точки относительно некоторой избранной точки (полюса –в терминологии теоретической механики) называется вектор: L= [ r, p ]. Здесь r – радиус-вектор материальной точки, начало которого совпадает с полюсом, а конец с материальной точкой, р – импульс материальной точки. Величину момента импульса часто удобно вычислять как произведение L= r mv,
где r – прицельное расстояние (или плечо импульса), равное расстоянию между полюсом и прямой, вдоль которой направлен вектор скорости частицы (см. рис. 2). 2. Моментом силы относительно полюса называется вектор: M= [ r, F ]. где F – сила, r – радиус-вектор, направленный от полюса к точке приложения силы. Точно так же, как и для момента импульса, величина момента силы может быть записана как произведение:
M =hF, где h – плечо силы, т.е. расстояние между полюсом и линией действия силы (рис. 3). 3. Связь между L и M дается уравнением моментов:
где M – момент сил, приложенных к данной материальной точке. Существенно, что L и М вычисляются относительно одного и того же полюса. 4. Момент импульса аддитивен. Момент импульса системы материальных точек равен сумме моментов отдельных точек, составляющих систему. Все моменты должны определяться относительно одного полюса. 5. Производная по времени от момента импульса системы точек определяется уравнением моментов:
где М внеш – сумма моментов внешних сил, действующих на точки системы. Из этого уравнения следует, что момент импульса замкнутой системы тел сохраняется. Данное утверждение носит название закона сохранения момента импульса. 6. Моментом импульса или моментом силы относительно оси называется проекция соответствующего момента на эту ось. При этом полюс обязательно должен лежать на оси. 7. Для момента импульса системы точек справедливо равенство: L = [ R ци, P ] + L 0, где L 0 – момент импульса системы точек относительно ее центра масс, R ци – радиус–вектор центра масс системы, Р – импульс системы. Это соотношение называют теоремой Кёнига для момента импульса. 8. Момент системы сил, определяется как сумма моментов сил, приложенных к точкам системы. Как и момент каждой сил, составляющих систему сил, он зависит от выбора полюса, относительно которого вычисляются эти моменты: M = [ R, F ] + M ', где M – момент системы сил относительно старого полюса О, M '– момент импульса системы точек относительно нового полюса О’, R – радиус-вектор направленный от старого полюса к новому, F – сумма сил, приложенных к точкам системы (Рис. 4). Как видим, в случае F = 0, момент системы сил не зависит от выбора полюса. Таким свойством обладает в частности пара сил, т.е. система двух равных по величине и противоположных по направлению сил.
Рис. 4 Момент пары, как нетрудно убедиться, направлен перпендикулярно плоскости, в которой лежат силы, составляющие пару, в направлении, совпадающем с направлением перемещения буравчика (винта), вращаемого этой парой. Величина момента пары равна произведению величины сил, составляющих пару на расстояние между линиями действия этих сил. Это расстояние называется плечом пары сил или просто: плечом пары. 9. Если тело движется в центральном поле, то момент силы, действующей на тело в этом поле, относительно центра поля равен нулю. Поэтому момент импульса тела относительно центра поля постоянен. Задача 1 Шайба движется по гладкой горизонтальной плоскости и испытывает в точке 0 упругий удар с гладкой неподвижной стенкой. Найти точки, относительно которых момент импульса шайбы остается постоянным в этом процессе. Угол между направлением скорости шайбы и нормалью к стенке равен a. Решение Движение шайбы представлено на рис.1. Так как стенка гладкая то F тр = 0, и N – сила реакции при ударе направленная перпендикулярно стенке, ее момент равен нулю относительно любой точки, лежащей на прямой OO ', перпендикулярной стенке. Согласно уравнению моментов d L / dt = M. Так как относительно точек прямой ОО ' момент силы реакции M = 0, то d L / dt = 0 и L = const. Итак, момент импульса шайбы сохраняется относительно любой точки, лежащей на прямой ОО '. Другие силы, действующие на шайбу, как нетрудно понять, не изменяют ее момента (разберитесь с этим сами).
Задача 2 На гладкой горизонтальной плоскости лежат две небольшие одинаковые шайбы массы m каждая. Шайбы соединены друг с другом невесомой пружиной длины l 0 и жесткости k. В некоторый момент времени одной из шайб сообщили скорость v 0 в горизонтальном направлении, перпендикулярно пружине. Найти максимальное относительное удлинение пружины в процессе движения, если известно, что оно значительно меньше единицы. Решение
Поскольку шайбы движутся по гладкой горизонтальной плоскости, то сумма внешних сил – силы тяжести и силы реакции стола, действующих на каждую шайбу, равна нулю, поэтому такая система ведет себя как замкнутая, и в ней сохраняются импульс и момент импульса. Кроме того, в системе действуют лишь консервативные силы (силы упругости пружины), поэтому сохраняется ее энергия. Этих трёх законов сохранения достаточно, чтобы решить задачу. Удобнее всего делать это в системе отсчета, связанной с центром инерции. В этой системе отсчета сумма импульсов шайб равна нулю, откуда следует, что в любой момент времени скорости шайб равны по величине и направлены в противоположные стороны. Начальные скорости шайб относительно плоскости равны соответственно v 0 и нулю. Поэтому скорость центра инерции:
Скорости шайб по отношению к центру инерции равны, соответственно:
Причем скорости v 1 и v 2 направлены перпендикулярно пружине. Так как в начальный момент времени пружина не деформирована, то энергия системы относительно ее центра масс определяется в этот момент лишь кинетической энергией частиц:
Момент импульса L 1системы шайб относительно центра инерции в этот же момент времени равен:
Когда пружина окажется максимально растянутой, скорости шайб опять будут направлены перпендикулярно пружине, иначе шайбы удалялись бы или приближались друг к другу, т.е. длина пружины либо увеличивалась, либо уменьшалась бы, но, в любом из этих случаев, не была бы в этот момент максимальной. Если обозначить величину скорости шайб в этот момент через u ', длину пружины в этот момент через l ', то
В выражении для энергии второе слагаемое представляет собой потенциальную энергию растянутой на длину l’ – l 0 пружины. В силу законов сохранения энергии и момента импульса имеем следующие уравнения:
Выразив новую скорость шайб v’ из второго из этих уравнений, и подставив её в первое уравнение, найдём:
откуда приходим к уравнению:
После сокращения обеих частей уравнения на l’– l 0 получим:
а учитывая малую величину удлинения пружины (l’– l 0 << l 0), приходим к ответу:
Из полученного ответа видно, что удлинение пружины будет малым, если выполнено неравенство:
Задача 3 По гладкой горизонтальной плоскости движется небольшое тело массой m, привязанное к невесомой нерастяжимой нити, другой конец которой втягивают в отверстие O (рис. 1) с постоянной скоростью u. Найти угловую скорость тела в зависимости от расстояния r тела до отверстия, если в начальный момент оно находилось на расстоянии r 0, а угловая скорость нити была равна w0. Найти силу натяжения нити N как функцию расстояния r тела до отверстия О и площадь, которую опишет тело за один оборот. Решение
Поскольку сила тяжести, действующая на шарик, уравновешивается силой реакции стола, а момент силы N натяжения нити относительно точки O равен нулю, то момент импульса тела L относительно точки О сохраняется. Запишем выражение для момента импульса тела: L = [ r, p ] = m [ r, v ]. Разложим скорость тела v на две составляющие: v ' – поперек направления нити и u – вдоль нити (рис.2): v = v ' + u. Так как векторное произведение [ r, u ] = 0, то: L = m [ r, v ' + u ] = m [ r, v ']. Поскольку v’= w r, где w – угловая скорость, и векторы r и v ' взаимно ортогональны, то величина момента: L=mru '= mr 2w. Поскольку L = const, а в начальный момент w=w0, r= r 0, то: mr 2w = mr 02w0,
откуда:
Для нахождения величины силы натяжения нити N удобнее всего воспользоваться соотношением между скоростью изменения кинетической энергии тела Т и мощностью Р, действующих на него сил:
В нашем случае:
поэтому:
поскольку u=const. Так как
Производная dr / dt – это проекция скорости тела на направление нити (радиальное направление) и, поскольку нить укорачивается, т.е. тело приближается к отверстию со скоростью u, то dr / dt = – u. Окончательно:
Для мощности имеем: P= (N, v) = (N, u+v ') = (N, u) + (N, v ') = (N, u) = Nu. Здесь мы учли, что N и v ' взаимно ортогональны, а N и u направлены в одну и ту же сторону вдоль нити. Итак, получаем:
Найдём теперь площадь фигуры, которую опишет тело за один оборот (она затенена на Рис. 3). Для этого найдём площадь треугольника (он заштрихован на рис. 3), которую опишет нить за малый промежуток времени dt. Для этого учтём, что величина этой площади dS может быть записана как половина модуля векторного произведения векторов r и d s = v dt:
где L – величина момента импульса. Так как L=const, то искомая площадь:
где t – время одного оборота тела вокруг точки О. Осталось найти это время. Для этого учтём, что за один оборот нить повернётся на угол 2p. С другой стороны, угол поворота d j за малый промежуток времени dt равен произведению w dt. Угловая скорость найдена ранее:
Проинтегрировав это равенство по периоду, найдём:
Задача 4 Нить длины l с подвешенным к ней небольшим телом массы m отклонена от вертикали на угол a. Тело толкнули в горизонтальном направлении перпендикулярно нити. При его последующем движении угол отклонения нити в тот момент, когда скорость тела вновь была направлена горизонтально, оказался равным b. Найти начальную скорость тела, и скорость в точке, где нить была отклонена на угол b. Решение В процессе движения тела скорость его всё время остаётся перпендикулярной нити, так как нить нерастяжима. Это означает, что сила натяжения нити не совершает работы. Как следствие этого механическая энергия тела остаётся постоянной, так как только сила тяжести (она консервативна) совершает работу над телом.
Рис. 1 Рассмотрим теперь момент импульса тела, выбрав в качестве полюса, относительно которого определяем момент, точку подвеса О нити. Вектор момента импульса перпендикулярен плоскости, образуемой нитью и вектором скорости. Поскольку тело движется, эта плоскость непрерывно изменяет своё положение, следовательно, изменяется и вектор момента импульса. Так что вектор момента импульса тела не сохраняется. Однако, как нетрудно убедиться, проекция вектора момента импульса на вертикальное направление, то есть момент импульса относительно нити, будет сохраняться. Для этого рассмотрим момент сил, приложенных к телу относительно точки О. Этих сил две – сила реакции нити и сила тяжести. Но сила натяжения нити направлена вдоль нити, поэтому её момент равен нулю. Что касается момента силы тяжести M тяж = [ r, m g ], то он перпендикулярен как радиус–вектору r (направлению нити), так и вектору g. Но это означает, что момент силы тяжести всё время направлен горизонтально. Если мы запишем уравнение моментов относительно полюса О:
и спроецируем его на вертикальное направление (ось OZ), то получим:
т.е. Lz = const. В начальный момент: Lz=L 0×sina = mu 0 l sina. Примем, что в точке, где скорость тела вновь направлена горизонтально, нить отклонена на угол b. Но тогда точно так же: Lz=L 1×sinb = mu 1 l sinb. Здесь v 1 – скорость тела в новом положении. Закон сохранения момента импульса тогда запишется следующим образом: u 0 sina = u 1 sinb. Запишем теперь уравнение, выражающее закон сохранения энергии:
Исключив отсюда скорость u 1 с помощью закона сохранения момента импульса, получим:
Задача 5 По гладкой горизонтальной плоскости движется гантелька, состоящая из двух небольших шариков массой m и М, соединённых невесомым стержнем длины l. Шарик массы М испытывает абсолютно упругий удар о неподвижную стенку, поверхность которой перпендикулярна скорости шара. Найти скорости шариков после удара, считая, что до удара они двигались с одинаковыми скоростями, в направлении перпендикулярном стержню. Решение Поскольку удар упругий, то энергия гантельки сохраняется. Кроме того, сохраняется момент импульса гантельки относительно точки удара О со стенкой, поскольку момент силы реакции N относительно её точки приложения равен нулю. Запишем эти уравнения:
Здесь мы учли, что радиус-вектор шарика, испытавшего удар, коллинеарен вектору его скорости, поэтому момент импульса этого шарика относительно точки удара равен нулю.
Согласно второму из получившихся уравнений видим, что u 1 = u 0, тем самым u 2 = – u 0. Таким образом, первый шар сразу после удара не изменил своей скорости, а второй начал двигаться назад с прежней по величине скоростью. Это означает, что импульс этой гантельки изменился в результате удара:
Причина изменения импульса гантельки – импульс, переданный гантельке силой реакции стенки. Задача 6 При каких условиях метеорит, движущийся вдали от Земли со скоростью V 0, может упасть на поверхность Земли? Влиянием других небесных тел пренебречь. Решение Очевидно, падение метеорита на Землю возможно, если минимальное расстояние, на котором проходит его траектория от центра Земли не превышает радиуса Земли (см. Рис. 1). При движении тела в центральном поле его момент импульса относительно центра этого поля остаётся неизменным: mV 0r = mV 1 R (1),
здесь R – радиус Земли, r – прицельное расстояние метеорита относительно центра Земли, V 0и V 1 – скорость метеорита вдали и, соответственно, вблизи Земли. Помимо закона сохранения момента импульса, в данной задаче мы можем воспользоваться ещё и законом сохранения энергии, поскольку поле тяготения является консервативным полем. Потенциальную энергию тела в поле тяготения найдём из закона всемирного тяготения:
Здесь т и М – масса тела и, соответственно, масса того небесного тела, в поле тяготения которого это тело движется, G – постоянная всемирного тяготения, r – расстояние между телами, Fr – проекция силы тяготения на радиальное направление. Воспользовавшись соотношением между силой и потенциальной энергией, найдём после интегрирования по dr:
Здесь мы положили постоянную интегрирования равной нулю, что соответствует выбору потенциальной энергии равной нулю на бесконечном удалении от небесного тела (сравните с задачей 1 раздела 5 Движение точки в консервативных полях). Записывая выражение для энергии метеорита вдали от Земли и в точке касания её поверхности, получим:
Потенциальную энергию, при выбранной выше её нормировке, можно записать как – mgR, поскольку сила тяготения, действующая на тело, находящееся на поверхности Земли равна mg:
Тем самым уравнение закона сохранения энергии запишем в виде:
откуда найдём V 1:
Воспользовавшись законом сохранения момента импульса (1), получим с учётом найденной нами скорости V 1:
Заметим, что 2 mgR = V 22, где V 2– вторая космическая скорость. Тем самым:
Вторая космическая скорость для Земли V 2 составляет 11,2 км/с, а скорость метеоритов V 0 обычно заметно больше, её величина около 30 км/с. Тем самым, для того чтобы метеорит мог упасть на поверхность Земли, его прицельное расстояние должно быть не больше радиуса Земли. А вот для Юпитера, вторая космическая скорость которого более чем в 5 раз превосходит вторую космическую скорость для Земли, прицельное расстояние оказывается приблизительно в 2,5 раза больше радиуса Юпитера, т.е. приблизительно в 25–30 раз больше радиуса Земли.
ДИНАМИКА ТВЕРДОГО ТЕЛА 1. В механике абсолютно твёрдым телом – в дальнейшем просто твердым телом – называют систему материальных точек, расстояния между которыми всё время остаются неизменными.
2. Поступательным движением твёрдого тела называют такое его движение, при котором любая прямая, жестко связанная с телом остаётся параллельной себе самой. Прямая жестко связанная с телом это такая прямая, расстояние от любой точки которой до любой точки тела неизменно в процессе движения. 3. Вращательным движением твёрдого тела вокруг неподвижной оси называют такое его движение, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности, центры которых лежат на этой оси. Положение тела тогда задаётся углом его поворота вокруг этой оси. 4. Вектором угловой скорости твёрдого тела называется вектор w, направленный вдоль оси вращения твёрдого тела в ту же сторону, в какую перемещается буравчик, вращающийся вместе с телом (рис.1). Проекция вектора угловой скорости на направление оси вращения (ось OZ на Рис. 1) равна производной по времени от угла поворота твёрдого тела: w z = d j/ dt. Угол поворота считается положительным, если для наблюдателя, расположенного так, что ось вращения направлена к нему, поворот происходит против часовой стрелки. Соответственно, и проекция w z положительна, если для такого наблюдателя вращение тела происходит против часовой стрелки. 5. Вектор v i скорости произвольной точки твёрдого тела, вращающегося вокруг неподвижной оси, равен векторному произведению векторов угловой скорости и радиус-вектора этой точки: v i = [ w, r i ]. Начало координат при этом выбрано на оси вращения твёрдого тела (см. Рис. 1). Может быть ввести (перед пунктом 6) общий случай: вращение вокруг точки, то есть вращение вокруг вращающейся оси? В последней фразе пункта 6 присутствуют слова: "… вращения тела относительно центра масс." Или там поменять на "вращение тела вокруг неподвижной в (с.ц.и.) оси, проходящей через центр масс". 6. Произвольное движение твердого тела в каждый момент времени можно рассматривать как совокупность поступательного и вращательного движений (теорема Эйлера). Точку внутри твёрдого тела, через которую проходит ось вращения можно выбирать произвольно, при этом величина и направление вектора угловой скорости не зависят от выбора этой точки, скорость же поступательного движения тела совпадает со скоростью этой выбранной точки. Физически наиболее обусловлено и практически чаще всего наиболее удобно выбирать ось вращения так, чтобы она проходила через центр масс тела. Тогда движение твердого тела складывается из поступательного движения со скоростью центра масс этого тела и вращения тела относительно оси, проходящей через центр масс. 7. Кинетическая энергия Т твердого тела, вращающегося вокруг неподвижной оси равна:
где w – величина угловой скорости вращения, а I – момент инерции твёрдого тела относительно оси вращения, определяемый равенством:
Здесь D mi – массы "точек" твёрдого тела, a Ri – их расстояния от оси вращения ОО '. Момент инерции в задачах, связанных с вращением твёрдого тела играет роль подобную той, что играет масса тела при его поступательном движении. Под "точкой" твердого тела имеется ввиду физически бесконечно малый элемент объема тела с массой D mi. Суммирование производится по всем таким объёмам, на которые разбито тело.
8. Если известен I С – момент инерции твёрдого тела относительно некоторой оси OO, проходящей через его центр инерции, то I – момент инерции твердого тела относительно произвольной, но параллельной ей оси O'O' находится с помощью теоремы Штейнера: I=I С + md 2 где m – масса твёрдого тела, d – расстояние между осями. 9. В силу теоремы Эйлера для описания движения твёрдого тела необходимо знать скорость движения его центра инерции и угловую скорость вращения. Поэтому система уравнений, определяющих движение твёрдого тела, состоит из уравнения движения центра масс и уравнения моментов:
где М – масса твёрдого тела, а ци – ускорение его центра масс, F внеш – сумма внешних сил, приложенных к твёрдому телу, L – момент импульса твёрдого тела, М внеш – сумма моментов внешних сил, приложенных к нему. Заметим, что L и М внеш могут вычисляться как относительно центра масс, так и относительно любой другой точки (разумеется, при этом точка, относительно которой вычисляются L и М внеш должна быть одной и той же как для L, так и для М внеш).
10. Поскольку разложение движения твердого тела на поступательное и вращательное можно производить различными способами, то в некоторых задачах бывает удобно выбирать ось вращения таким образом, чтобы движение твердого тела представлялось как чистое вращение. Положение этой оси будет, вообще говоря, изменяться с течением времени, поэтому ее называют мгновенной осью вращения. 11. Вектор момента импульса твердого тела определяется как сумма моментов "точек" этого тела: L = S DL i. 12. Направление вектора момента импульса твердого тела, при вращении вокруг произвольной оси, не совпадает, вообще говоря, с направлением этой оси (Рис. 3). Однако в каждом твердом теле существуют три взаимно перпендикулярные оси, проходящие через его центр масс, при вращении вокруг которых векторы L и w совпадают по направлению. Такие оси носят название главных осей инерции. Если тело имеет ось симметрии, то она будет одной из главных осей инерции. Задача 1 Докажите, что при поступательном движении твёрдого тела все его точки движутся с одинаковыми скоростями. Решение
Выберем в теле произвольным образом две точки. Пусть это точки А и В. Обозначим их радиус–векторы r A и r В, а вектор, соединяющий их, обозначим как R. Тогда: r В = r A + R. Дифференцируя это равенство по времени (дифференцирование по времени обозначаем точкой), получим:
Но вектор R – постоянный вектор, так как, ни его длина, ни направление не изменяются. Действительно, расстояния между точками твёрдого тела неизменны, поэтому длина вектора R также неизменна. Кроме того, тело движется поступательно, поэтому направление вектора R также не изменяется. Поэтому производная вектора R равна нулю, тем самым:
Т.е. скорости выбранных нами точек одинаковы. Но в силу произвольности выбора этих точек, все точки тела имеют такие же скорости. Задача 2 Докажите, что кинетическую энергию твёрдого тела в самом общем случае можно представить в виде:
где Vци – скорость центра масс твердого тела, I С – момент инерции твёрдого тела относительно оси вращения, проходящей через центр масс твердого тела, w – угловая скорость вращения твёрдого тела. Решение Согласно теореме Кёнига кинетическую энергию твёрдого тела можно представить как:
Здесь M – масса тела, Vц – скорость его центра инерции, Т 0 – кинетическая энергия тела в системе отсчета, движущейся со скоростью центра инерции. Но в этой системе отсчёта центр инерции неподвижен. Следовательно, движение твёрдого тела в этой системе отсчёта есть вращение вокруг оси, проходящей через центр инерции тела, и кинетическая энергия такого движения равна:
где I С – момент инерции тела относительно оси вращения, проходящей через центр инерции тела, а w – угловая скорость вращения твёрдого тела. Тем самым утверждение доказано:
Задача 3 Докажите, что кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси, связана с вектором момента импульса L этого тела и вектором угловой скорости w его вращения следующим образом:
Полюс, относительно которого определяется момент импульса, выбран на оси вращения тела. Решение Вектор момента импульса твердого тела определяется как сумма моментов "точек" этого тела:
Преобразуем двойное векторное произведение под знаком суммы с помощью известного тождества: [ a,[ b, c ]] = b (a, c) – c (a, b).
Эта формула показывает, что направления векторов L и w, вообще говоря, не совпадают, поскольку в самом общем случае сумма Умножим теперь обе части полученного выражения скалярно на вектор w:
Здесь Iz – момент инерции тела относительно оси вращения OZ. Поделив обе части полученного соотношения на 2, придём к искомому результату:
Поскольку Твращ > 0, то угол между вектором момента импульса L и вектором угловой скорости w может быть только острым. Полученный результат можно записать несколько по-иному, имея в виду, что
Здесь Lz – проекция момента импульса тела на направление оси вращения OZ. Сократив обе части полученного равенства на w/2, получим: Lz = Iz w. Как видим, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость вращения вокруг этой оси. Задача 4 Докажите, что кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси, связана с проекциями вектора угловой скорости w на главные оси твёрдого тела и моментами инерции относительно главных осей следующим образом:
Решение Согласно результату предыдущей задачи, кинетическая энергия вращающегося твёрдого тела связана с его моментом импульса:
Если выбрать какие-либо оси координат, связанные с этим телом, то тогда:
Вообще говоря, каждая проекция момента импульса зависит от всех трёх проекций угловой скорости на оси координат. Однако если в качестве системы координат выбрать систему, оси которой являются главными осями тела, то, согласно свойствам этих осей:
Тем самым:
Задача 5 Как зависит скорость изменения кинетической энергии твёрдого тела, т.е. производная dT / dt, от сил, приложенных к этому телу? Решение Согласно теореме Кёнига и результату предыдущей задачи, кинетическая энергия твёрдого тела может быть записана в виде:
Здесь Ix, Iy, Iz – моменты инерции твёрдого тела относительно главных осей, а w x, w y,w z – проекции вектора угловой скорости на эти оси. Продифференцировав это равенство по времени, получим:
Здесь мы учли, что
Здесь F внеш и М внеш векторная сумма внешних сил и, соответственно, векторная сумма моментов внешних сил, приложенных к телу. Как видим, изменение кинетической энергии твёрдого тела определяется как внешними силами, так и моментами этих сил. Причём, что интересно, ответ не зависит от того, в каких именно точках тела приложены действующие на тело силы. Всё определяется векторной суммой внешних сил и скоростью движения центра инерции тела, и, соответственно, векторной суммой моментов внешних сил, приложенных к телу и угловой скоростью вращения тела:
Поскольку производная dT / dt равна мощности сил, действующих на тело, то полученный результат представляет мощность внешних сил, приложенных к твёрдому телу:
Задача 6
Рассмотрим плоское твёрдое тел
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2007; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.253.21 (0.011 с.) |

 Рис. 1
Рис. 1
 Рис. 2
Рис. 2
 Рис. 3
Рис. 3
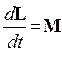

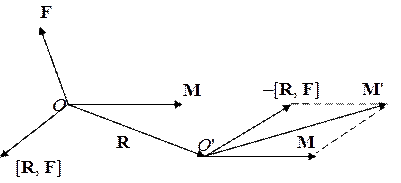
 Рис. 1
Рис. 1


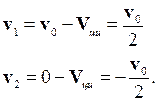
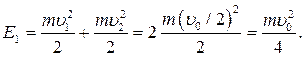










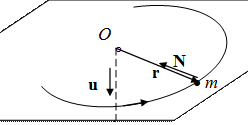 Рис. 1
Рис. 1
 Рис. 2
Рис. 2
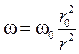 .
.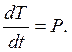


 , то:
, то:




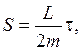
 Рис. 3
Рис. 3
 .
.


 ,
, ,
, .
.
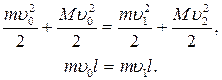
 Рис. 1
Рис. 1

 Рис. 1
Рис. 1


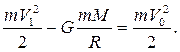

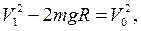

 .
. .
. Рис. 1
Рис. 1

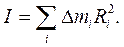
 Рис. 2
Рис. 2

 Рис. 3
Рис. 3
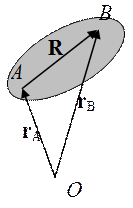 Рис. 1
Рис. 1
 .
.
 ,
,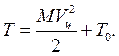

 .
.

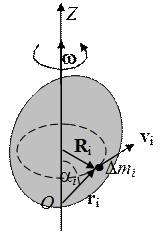 Рис. 1
Рис. 1

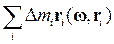 представляет собой вектор, направление которого не обязано совпадать с направлением вектора угловой скорости.
представляет собой вектор, направление которого не обязано совпадать с направлением вектора угловой скорости.

 :
: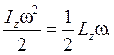







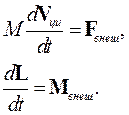


 Рис. 1
Рис. 1



