Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Применение уравнения Шредингера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Уравнение Шредингера для гармонического осциллятора. Энергия осциллятора, напишите выражение и нарисуйте схему энергетических уровней. Нулевая энергия. Как можно качественно объяснить нулевую энергию на основе соотношения неопределенностей?
В классической физике гармоническим осциллятором называют частицу, совершающую движения по закону синуса или косинуса. Потенциальная энергия такой частицы:
Dх»А - неопределенность в координате примем равной амплитуде А колебаний. Dр»р=m
2. Напишите уравнение Шредингера и его решение для частицы в одномерном потенциальном ящике с бесконечно высокими стенками. Найдите выражение для энергии частицы.
Частица массой m, находятся в потенциальной яме, например, электрон в металле. Чтобы решить уравнение Шрёдингера введем следующие упрощения: 1)Частица находится в прямоугольной потенциальной яме, внутри ямы потенциальная энергия U постоянна, примем ее равной нулю. Высота стенок ямы ®¥, т.е. частица не может выйти из ямы. 2)Частица может двигаться только по оси х в пределах ширины ямы а, т.е. 0£х£а (одномерная задача). Уравнение Шрёдингера для частицы в прямоугольной пот. яме: При решении этого уравнения нам нужно найти пси-функцию y(х) и энергию Е частицы. По форме - это уравнение колебаний. Решение такого дифференциального уравнения имеет вид: Для нахождения коэффициентов А и В используем краевое условие: Величину w найдем из второго краевого условия:
Найдём вторую производную пси-функции и поставим в уравнение Шрёдингера, получим: 3. Напишите уравнение Шредингера и его решение для электрона в атоме водорода в основном состоянии. Что такое радиальная плотность вероятности
В этом случае используются сферические координаты: радиус-вектор r и угловые координаты j и q. Уравнение Шрёдингера для электрона в атоме водорода в основном состоянии:
r называется радиальной плотностью вероятности, по смыслу - это вероятность обнаружить электрон в сферическом слое единичной толщины.
Максимальная вероятность обнаружить электрон при наименьшей его энергии совпадает с 1-ым боровским радиусом а. Энергия электрона в атоме водорода квантуется, выражение для нее получается такое же, как в теории Бора.
Тема 8. Квантовые числа. 1. Квантовые числа n, l, m, ms и их связь с физическими характеристиками состояния электрона.
Состояние электрона в квантовой системе полностью описывается с помощью 4-х квантовых чисел: n, l, m, mS. 1)n=1,2,3,…,¥ - главное квантовое число входит в выражение для энергии электрона. 2)l=0,1,2,…,(n-1) - орбитальное квантовое число входит в выражения для орбитальных механического LОРБ и магнитного pОРБ моментов электрона в атоме. Показывает, что орбитальные моменты квантуются, т.е. могут принимать только дискретные значения.
3)m=-l,...,-1,0,+1,...,+l - магнитное квантовое число входит в выражение для проекций орбитальных моментов на направление Z внешнего поля. Показывает, что плоскость, в которой движется электрон во внешнем поле ориентируется только определенным образом, так чтобы проекции моментов были кратны
4)
2. Получите выражение, связывающее механический и магнитный моменты орбитального движения электрона в атоме. Напишите условия квантуемости этих моментов. Магнетон Бора. Гиромагнитное отношение. 1)
Гиромагнитное отношение: 2)Орбитальные моменты квантуются, т.е. могут принимать только дискретные значения:
Магнетон Бора (магн. моменты принято выражать в магнетонах бора): 3. Проекции орбитальных и собственных моментов электрона на направление внешнего поля. Квантуемость этих величин. Спин электрона. Опыты Штерна и Герлаха. Как следует понимать выражения «частица с целым или полуцелым спином»? 1)
2)
Спин - собственный механический момент (момент импульса) электрона s=1/2 - спиновое квантовое число.
В квантовой механике различают частицы с «целым» спином (бозоны) и «полуцелым» спином (фермионы). Подразумевается, что проекция спина либо кратна
4. Принцип Паули. Периодическая система элементов Д.И. Менделеева. Последовательность заполнения электронами энергетических оболочек атомов. Формула электронной конфигурации атомов. Как объясняются нарушения последовательности заполнения оболочек?
Принцип Паули: «Никакие два электрона в атоме не могут находиться в одном и том же квантовом состоянии, каждый электрон должен иметь свой набор квантовых чисел n, l, m, mS». Принципу Паули подчиняются микрочастицы, которые имеют полуцелый спин - электрон, протон, нейтрон, нейтрино. Частицы с полуцелым спином называют фермионами. Принцип Паули объясняет, почему электроны в многоэлектронных атомах образуют энергетические оболочки и подоболочки. Кол-во эл. с одинак. n, l, m, mS: 1 Кол-во эл. с одинак. n, l, m: 2 Кол-во эл. с одинак. n, l: 2(2l+1) Кол-во эл. с одинак. n, алгебр. сумму: Распределение электронов в атомах определяется: 1. принципом Паули; 2. принципом наименьшей энергии. Заполнение оболочек атомов: 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 4f14 и т.д. K L M N Здесь 1,2,3,4… - главные квантовые числа n; s,p,d,f… - буквенные обозначения орбитальных квантовых чисел l (подоболочки); K,L,M,N... - оболочки. Верхние индексы - количество электронов с данными n и l. Сумма верхних чисел дает общее количество электронов в данном атоме. Подобное распределение является идеализированным (против правила Клечковского). Оно было бы таким, если бы каждый электрон в атоме взаимодействовал только с ядром атома. В действительности данный электрон испытывает действие остальных электронов атома. Часто энергетически выгодным оказывается состояние, когда нижняя оболочка заполнена не полностью, а начинает заполняться следующая. Нарушения в заполнении электронных оболочек атомов наблюдаются у № 19 - калий и более тяжелых элементов.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 956; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.008 с.) |

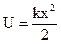 , частота колебаний
, частота колебаний  .
. Уравнение Шрёдингера для гармонического осциллятора:
Уравнение Шрёдингера для гармонического осциллятора: 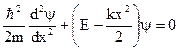
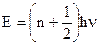 - полная энергия квантового осциллятора n=0,1,2,…,¥.
- полная энергия квантового осциллятора n=0,1,2,…,¥.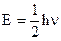 - эта величина называется нулевой энергией осциллятора n=0.
- эта величина называется нулевой энергией осциллятора n=0.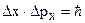 - соотношение неопределенностей.
- соотношение неопределенностей. =mwА - неопределенность в импульсе примем равной самому импульсу; максимальная скорость колебаний
=mwА - неопределенность в импульсе примем равной самому импульсу; максимальная скорость колебаний 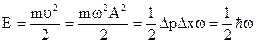 - нулевая энергия осциллятора.
- нулевая энергия осциллятора.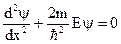 .
.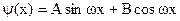 .
.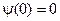 , смысл которого в том, что частица не может выйти из ямы.
, смысл которого в том, что частица не может выйти из ямы. 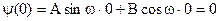 отсюда следует:
отсюда следует: 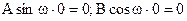 т.к. sin0=0, а cos0=1¹0, то В=0. Таким образом, получаем:
т.к. sin0=0, а cos0=1¹0, то В=0. Таким образом, получаем: 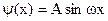 .
.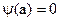 , следовательно:
, следовательно:  , отсюда:
, отсюда: 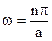 , n=1,2,3… Окончательно имеем:
, n=1,2,3… Окончательно имеем: 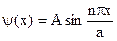 . А найдем из усл. норм.:
. А найдем из усл. норм.: 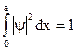 .
.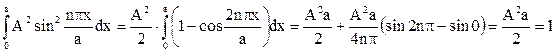 , отсюда:
, отсюда:  .
. - пси-функция для частицы в одномерной прямоугольной потенциальной яме.
- пси-функция для частицы в одномерной прямоугольной потенциальной яме. - энергия частицы в одномерной потенциальной яме.
- энергия частицы в одномерной потенциальной яме. ? Нарисуйте график
? Нарисуйте график  , где r - радиальная координата; дайте пояснения.
, где r - радиальная координата; дайте пояснения.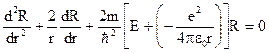 ,
, 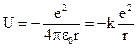 - пот. энергия электрона в атоме Н Z=1 (
- пот. энергия электрона в атоме Н Z=1 (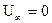 ).
). Решение уравнения:
Решение уравнения: 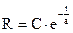 ;
; 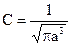 ;
; 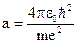 - первый боровский радиус.
- первый боровский радиус.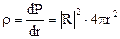 ;
; 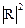 - плотность вероятности;
- плотность вероятности;  - площадь сферы.
- площадь сферы. - механический орбитальный момент (момент импульса).
- механический орбитальный момент (момент импульса).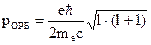 - магнитный орбитальный момент.
- магнитный орбитальный момент. или
или 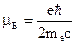 .
.
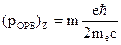
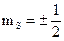 - магнитное собственное квантовое число входит в выражение для проекций собственного механического LСОБСТ и магнитного рСОБСТ моментов на направление Z внешнего поля. Показывает, что ориентация собственных моментов может иметь только два значения.
- магнитное собственное квантовое число входит в выражение для проекций собственного механического LСОБСТ и магнитного рСОБСТ моментов на направление Z внешнего поля. Показывает, что ориентация собственных моментов может иметь только два значения.

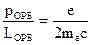 - отношение орбитальных магнитного и механического момента (как вектор векторы они направлены противоположно, НАСЧЁТ МИНУСА - ВОПРОС).
- отношение орбитальных магнитного и механического момента (как вектор векторы они направлены противоположно, НАСЧЁТ МИНУСА - ВОПРОС).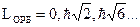
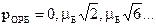
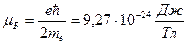 .
.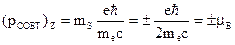 - проекция собственного магнитного момента на направл. Z (2 зн).
- проекция собственного магнитного момента на направл. Z (2 зн). , связанный с вращением электрона вокруг собственной оси.
, связанный с вращением электрона вокруг собственной оси.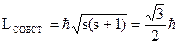 имеет только одно значение.
имеет только одно значение.