
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы квантовой статистики и физики твердого тела.Содержание книги
Поиск на нашем сайте
Тема 9. Классическая и квантовые статистики. 1. Статистическое описание ансамблей множества частиц. Различимость и неразличимость тождественных частиц. Больцмановское распределение молекул газа по энергиям.
В классической статистике частицы считаются различимыми друг от друга. В квантовой механике считается, что однотипные частицы, например, электроны, имеют совершенно одинаковые свойства - массу, электрический заряд, спин и считаются неразличимыми. Классическая статистика Максвелла-Больцмана применяется в молекулярно-кинетической теории к молекулам газа. Закон распределения молекул по энергиям (закон Больцмана) имеет вид:
2. Бозоны и фермионы. Распределение Бозе-Эйнштейна. Сверхпроводимость и сверхтекучесть. Практическое применение сверхпроводимости.
Одни квантовые частицы имеют целые спины - их называют бозонами, поведение бозонов описывается симметричными пси-функциями, а статистику называют статистикой Бозе-Эйнштейна. Бозоны не подчиняются принципу Паули. Квантовая статистика Бозе-Эйнштейна описывает поведение бозонов - частиц с целым или нулевым спином. Например, атом водорода состоит из электрона и протона, имеющих полуцелые спины. Но спины могут быть либо параллельными, либо антипараллельными, поэтому атом водорода в нормальном состоянии будет бозоном. Ядро атома гелия-4 (
Бозоны не подчиняются принципу Паули, т.е. данное значение энергии могут иметь многие бозоны в системе.
Сверхтекучесть В 1938 году П.Л. Капица открыл явление сверхтекучести гелия. Гелий уникален тем, что даже при самых низких температурах он не затвердевает, оставаясь жидким.
В области температур от 4,2К до 2,18К (l-точка) гелий ведет себя как обычная жидкость, и в этой области температур его называют гелий-I. Ниже l-точки гелий становится сверхтекучим, и его называют гелий-II. Одно из свойств сверхтекучего гелия является способность проводить тепло без каких-либо потерь. В сверхтекучем гелии отсутствует вязкость, он беспрепятственно протекает через самые узкие капилляры. Атом гелия имеет нулевой спин, т.е. является бозоном и, следовательно, не подчиняется принципу Паули. При понижении температуры энергия атома гелия понижается, и при достаточно низкой температуре все атомы оказываются в наинизшем возможном энергетическом состоянии. Но если все атомы имеют одну и ту же энергию, то они имеют и одну волновую функцию. Таким образом, атомы сверхтекучего гелия действуют согласованно, как единое целое. Энтропия (мера внутренней неупорядоченности) сверхтекучего гелия равна нулю. Сверхпроводимость
Квантовая теория сверхпроводимости был разработана Бардиным, Купером и Шриффером (теория БКШ). Сверхпроводимость наблюдается для частиц, которые являются бозонами, т.е. имеющими нулевой или целый спин. В сверхпроводнике при некоторых условиях электроны проводимости объединяются попарно, при этом у них противоположно направлены спины, и они становятся бозонами. При некоторой критической температуре все пары-бозоны оказываются в наинизшем энергетическом состоянии и имеют одну и ту же волновую функцию. Использование сверхпроводников в технике и для научных исследований имеют большие перспективы, т.к. при этом снижаются до минимума потери на джоулево тепло. Сверхпроводники работают на постоянном токе. Многие трудности были бы преодолены, если бы удалось создать сверхпроводник при более высоких температурах, в идеале - при комнатной температуре, но пока максимальная температура 125К.
3. Распределение Ферми-Дирака электронов по энергиям в металлах. Напишите выражение, поясните все величины, приведите графики для температур T=0 К и Т>0 К. Энергия Ферми. Средняя энергия электронов при температуре, близкой к абсолютному нулю.
Квантовая статистика Ферми-Дирака описывает поведение фермионов - частиц с полуцелым спином. К фермионам относятся электроны, протоны, нейтроны, нейтрино, ядра атома гелия-3. Основное отличие статистики ФД в том, что данное значение энергии может иметь только один электрон. Закон распределения частиц по энергиям в статистике ФД имеет вид:
При температуре Т>0К электроны за счет энергии теплового движения «покидают» свои уровни и переходят на более высокие. Для металлов энергия Ферми определяется следующим образом: 1)При Т=0К - это уровень энергии, отделяющий заполненные электронами уровни от незаполненных или это максимальная энергия электронов при Т=0К. 2)При Т>0К - это энергетический уровень, который занимает электрон с вероятностью, равной 1/2. При высоких температурах или малых концентрациях электронов распределение ФД переходит в классическое распределение МБ: Е-ЕF>>кТ. - Энергия Ферми при Т=0К, не зависит от числа электронов в образце и его объема, а определяется только концентрацией электронов n=N/V: - Для металлов энергия Ферми очень слабо зависит от температуры (kT/E0F@0,01 при комнатных температурах): Средняя энергия электронов в зоне проводимости связана с энергией Ферми:
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.165 (0.011 с.) |



 -частица) - тоже бозон, т.к. состоит из 2-х протонов и 2-х нейтронов. Сам атом гелия-4 тоже бозон, т.к. у него два электрона. Но ядро атома гелия-3, состоящее из двух протонов и одного нейтрона не является бозоном. К бозонам относятся также фотоны и мезоны.
-частица) - тоже бозон, т.к. состоит из 2-х протонов и 2-х нейтронов. Сам атом гелия-4 тоже бозон, т.к. у него два электрона. Но ядро атома гелия-3, состоящее из двух протонов и одного нейтрона не является бозоном. К бозонам относятся также фотоны и мезоны.
 В 1911 году Камерлинг-Оннес обнаружил, что при температуре 7,2К сопротивление свинца внезапно становится равным нулю и свинец становится сверхпровдником. Очень важно, чтобы вещество было чистым, без посторонних примесей.
В 1911 году Камерлинг-Оннес обнаружил, что при температуре 7,2К сопротивление свинца внезапно становится равным нулю и свинец становится сверхпровдником. Очень важно, чтобы вещество было чистым, без посторонних примесей.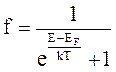
 На рисунках показаны графики функции ФД, их часто называют распределением электронов по энергиям. При температуре Т=0К вероятность того, что электрон имеет какое-либо значение энергии в пределах 0¸EF равна единице; вероятность обнаружить электрон с энергией > EF равна нулю.
На рисунках показаны графики функции ФД, их часто называют распределением электронов по энергиям. При температуре Т=0К вероятность того, что электрон имеет какое-либо значение энергии в пределах 0¸EF равна единице; вероятность обнаружить электрон с энергией > EF равна нулю. .
. .
. .
.


