
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямые и плоскости в пространстве. Различные уравнения прямой и плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Всякое уравнение первой степени относительно координат x, y, z Ax + By + Cz +D = 0 (1) задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (1), которое называется уравнением плоскости. Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (1) коэффициенты A, B, C одновременно не равны 0. Особые случаи уравнения (1): 1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат. 2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz. 3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz. 4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz. Уравнения координатных плоскостей: x = 0, y = 0, z = 0. Прямая в пространстве может быть задана: 1) как линия пересечения двух плоскостей,т.е. системой уравнений: A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (2) 2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями: 3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями: Уравнения (4) называются каноническими уравнениями прямой. Вектор a называется направляющим вектором прямой. Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: x = x1 +mt, y = y1 + nt, z = z1 + рt. (5) Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой: x = mz + a, y = nz + b. (6) От уравнений (6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения: От общих уравнений (2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [ n 1, n 2], где n 1(A1, B1, C1) и n 2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система равносильна системе Система
Линии второго порядка. Линии второго порядка, плоские линии, декартовы прямоугольные координаты, которых удовлетворяют алгебраическому уравнению 2-й степени a11x2 + a12xy + a22y2 + 2a13x + 2a23y + a11 = 0. (*) Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно, не распадающиеся линии:
y2 = 2px — параболы,
распадающиеся линии:
x2 - а2 = 0 — пары параллельных прямых, x2 + а2 = 0 — пары мнимых параллельных прямых, x2 = 0 — пары совпадающих параллельных прямых. Поверхность второго порядка Пусть в пространстве задана прямоугольная декартова система координат. Поверхностью второго порядка называется поверхность, определяемая уравнением
где 1. Сфера Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром. Теорема. Сфера радиуса
2. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид где
Рис. Эллипсоид 3. Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
Рис. Однополостный гиперболоид 5. Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
Рис. Изображение конуса с помощью сечений 6. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
Рис. Эллиптический параболоид 7. Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими. Рассмотрим уравнение вида и покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси Заметим, что на плоскости Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение. Поверхность, которая в некоторой декартовой системе координат задается уравнением 4?. Евкливоды п -мерные пространства Если координаты векторов
заданы в ортонормированном базисе, то скалярное произведение вычисляется по формуле
Аналогичной формулой можно задать и скалярное произведение в Пусть
Скалярное произведение векторов, обозначается оно обычно В отличие от обычного трехмерного пространства, где с помощью транспортира и линейки можно измерить угол между векторами и длину вектора, в Если
Предоставляем читателю самостоятельно убедиться в совпадении этой формулы с формулой (1) Вещественное линейное пространство, в котором задано скалярное произведение называется евклидовым пространством. В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя
В трехмерном пространстве с помощью скалярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в Два вектора евклидова пространства называются ортогональными, если их скалярное произведение равно нулю. Если
где черта над Комплексное линейное пространство, в котором введено скалярное произведение, называется унитарным пространством. В унитарном пространстве модуль вектора и условие ортогональности вводятся с помощью скалярного произведения так же, как в евклидовом пространстве. В координатной записи
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

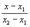 =
= 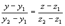 ; (3)
; (3)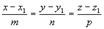 . (4)
. (4)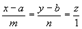 .
.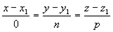
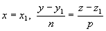 ; такая прямая перпендикулярна к оси Ох.
; такая прямая перпендикулярна к оси Ох.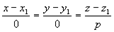 равносильна системе x = x1, y = y1; прямая параллельна оси Oz.
равносильна системе x = x1, y = y1; прямая параллельна оси Oz.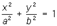 — эллипсы,
— эллипсы,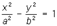 — гиперболы,
— гиперболы,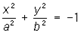 — мнимые эллипсы;
— мнимые эллипсы;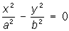 — пары пересекающихся прямых,
— пары пересекающихся прямых,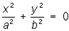 — пары мнимых пересекающихся прямых,
— пары мнимых пересекающихся прямых,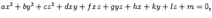 (1)
(1)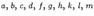 - вещественные числа, причем хотя бы одно из чисел
- вещественные числа, причем хотя бы одно из чисел 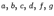 отлично от нуля.
отлично от нуля.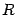 с центром в точке
с центром в точке 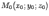 имеет уравнение
имеет уравнение 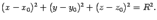
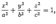
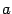 ,
,  ,
,  -- положительные числа.
-- положительные числа.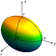
 где
где 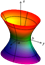
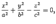 где
где 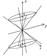
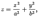 где
где 
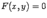
 . Пусть
. Пусть 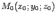 -- некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная
-- некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная 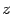 , ему будут удовлетворять координаты всех точек
, ему будут удовлетворять координаты всех точек  , где
, где 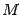 лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку
лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку 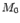 параллельно оси
параллельно оси 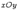 уравнение определяет направляющую рассматриваемой цилиндрической поверхности.
уравнение определяет направляющую рассматриваемой цилиндрической поверхности.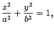 называется эллиптическим цилиндром, поверхность, которая задается уравнением
называется эллиптическим цилиндром, поверхность, которая задается уравнением 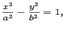 называется гиперболическим цилиндром, а которая задается уравнением
называется гиперболическим цилиндром, а которая задается уравнением 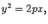 называется параболическим цилиндром.
называется параболическим цилиндром.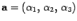 и
и 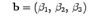
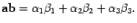
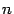 -мерном пространстве.
-мерном пространстве.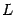 -- вещественное
-- вещественное  . Тогда векторы
. Тогда векторы 
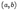 , задается формулой
, задается формулой 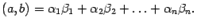 (1)
(1)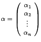 ,
, 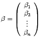 -- координатные столбцы векторов
-- координатные столбцы векторов 
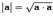 . В евклидовом пространстве модуль вектора определим аналогично
. В евклидовом пространстве модуль вектора определим аналогично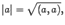 то есть
то есть 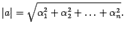
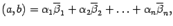
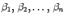 означает комплексное сопряжение.
означает комплексное сопряжение.



