
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 14. Нормальное уравнение прямой. Расстояние от точки до прямойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р. Если
уравнение этого вида называется нормальным.
Пусть дана какая-нибудь прямая и произвольная точка
Таким образом, чтобы найти отклонение какой-нибудь точки Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: Если дано общее уравнение прямой
Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.
Глава 15. Уравнение пучка прямых Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром в S. Если
где Более того, в уравнении (1) числа Если
Этим уравнением можно определить любую прямую пучка с центром S, кроме той, которая соответствует
Глава 16. Полярное уравнение прямой Прямая, проведенная через полюс перпендикулярно к данной прямой, называется ее нормалью. Обозначим буквой Р точку, в которой нормаль пересекает прямую; установим на нормали положительное направление от точки О к точке Р. Угол, на который нужно повернуть полярную ось до наложения ее на отрезок
Глава 17. Окружность Уравнение
определяет окружность радиуса R с центром C( Если центр опружности совпадает с началом координат, то есть если
Глава 18. Эллипс Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид
где
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью. Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае Число
где а - большая полуось, называется эксцентриситетом эллипса. Очевидно,
Если эллипс определен уравнением (1) и
(рис.) называются директрисами эллипса (если Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:
Если две плоскости
(рис.).
Если круглый цилиндр имеет в качестве направляющей окружность радиуса b, то в сечении этого цилиндра плоскостью, наклоненной к оси цилиндра под острым углом
(рис.).
Глава 19. Гипербола Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид
где
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы. Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть
Уравнение
определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b. Две гиперболы, которые определяются уравнениями
в одной и той же системе координат, называются сопряженными. Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид
Число
где а - расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы
фокальные радиусы точек левой ветви - по формулам
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями
Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:
Глава 20. Парабола Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы. Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
Фокальный радиус произвольной точки М(x; y) параболы (то есть длина отрезка F(M) может быть вычислен по формуле
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости. Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат - с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
если она лежит в верхней полуплоскости (рис.), и
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.30.14 (0.009 с.) |

 - полярный угол нормали, р - длина отрезка
- полярный угол нормали, р - длина отрезка 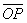 (рис.), то уравнение данной прямой может быть записано в виде
(рис.), то уравнение данной прямой может быть записано в виде ;
;
 ; обозначим через d расстояние от точки М* до данной прямой. Отклонением
; обозначим через d расстояние от точки М* до данной прямой. Отклонением  точки
точки  ,
,  точки
точки  .
.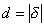 .
. , то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель
, то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель  , определяемый формулой
, определяемый формулой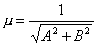 .
. и
и  - уравнения двух прямых, пересекающихся в точке S, то уравнение
- уравнения двух прямых, пересекающихся в точке S, то уравнение , (1)
, (1) - какие угодно числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S.
- какие угодно числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S. , то, деля обе части уравнения (1) на
, то, деля обе части уравнения (1) на  , получим
, получим . (2)
. (2) , то есть кроме прямой
, то есть кроме прямой (1)
(1) , то уравнение (1) принимает вид
, то уравнение (1) принимает вид
 и
и  , расстояние между ними - через 2с. По определению эллипса
, расстояние между ними - через 2с. По определению эллипса  или
или  .
. (1)
(1) ; очевидно,
; очевидно,  . Уравнение вида (1) называется каноническим уравнением эллипса.
. Уравнение вида (1) называется каноническим уравнением эллипса.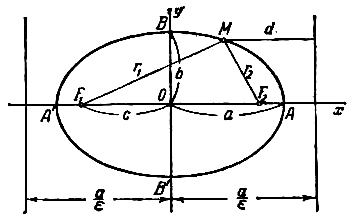
 ; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.
; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.
 (для окружности
(для окружности  ). Если М(x; y) - произвольная точка эллипса, то отрезки
). Если М(x; y) - произвольная точка эллипса, то отрезки  и
и  (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам
(рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам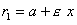 ,
,  .
.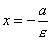 ,
, 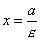
 ,
,  .
.
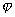 , то проекциейй на плоскость
, то проекциейй на плоскость 



 , или
, или 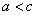 .
. (1)
(1) . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.
. Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.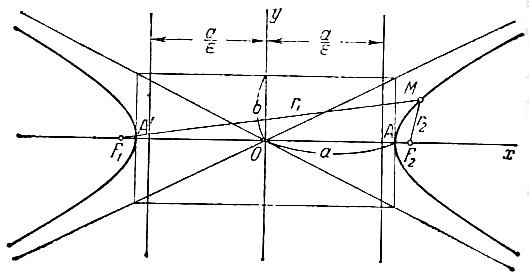
 ,
, 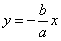
 (2)
(2)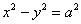 или
или 
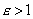 . Если М(x; y) - произвольная точка гиперболы, то отрезки
. Если М(x; y) - произвольная точка гиперболы, то отрезки  и
и  (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
(см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам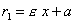 ,
,  ,
, ,
,  .
.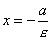 ,
, 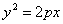 (1)
(1)
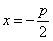 .
. .
.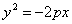 (2)
(2)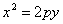 (3)
(3)
 (4)
(4)



