

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Уравнение прямой линии в пространстве
Положение некоторой прямой линии  в пространстве можно задать разными способами (о них шла речь в предыдущем параграфе). Прямая линия может определяться, например, как линия пересечения двух заданных (своими уравнениями) плоскостей в пространстве можно задать разными способами (о них шла речь в предыдущем параграфе). Прямая линия может определяться, например, как линия пересечения двух заданных (своими уравнениями) плоскостей  и и 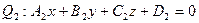 , которые, конечно, не должны быть параллельными. В соответствии с (1) предыдущего параграфа, уравнения этих плоскостей, объединенные в систему, будут называться общими уравнениями прямой , которые, конечно, не должны быть параллельными. В соответствии с (1) предыдущего параграфа, уравнения этих плоскостей, объединенные в систему, будут называться общими уравнениями прямой  : :
(1) 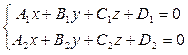 . .
В этом случае прямая состоит только из тех точек пространства, координаты  и и 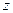 которых удовлетворяют системе (1) (т.е. находятся одновременно на каждой плоскости которых удовлетворяют системе (1) (т.е. находятся одновременно на каждой плоскости 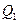 и и 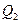 ). Ясно, что одна и та же прямая может быть пересечением многих пар плоскостей. Поэтому общие уравнения прямой определяются самой прямой не однозначно. ). Ясно, что одна и та же прямая может быть пересечением многих пар плоскостей. Поэтому общие уравнения прямой определяются самой прямой не однозначно.
Во многих случаях общие уравнения прямой "неудобны" для решения задач, связанных с этой прямой. Например, чтобы найти координаты какой-нибудь точки на прямой по ее общим уравнениям (1), нужно провести довольно хлопотные вычисления. А именно, нужно задать произвольно какую-нибудь координату (например, 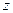 ), подставить ее в систему (1) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты ( ), подставить ее в систему (1) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты ( и и  ). Причем, может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты. ). Причем, может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.
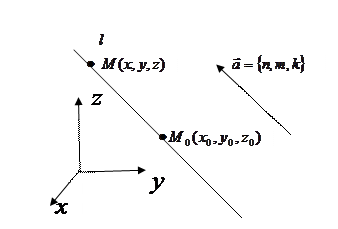 Можно задать прямую линию в пространстве и другим способом (см. рисунок). Очевидно, что положение любой прямой Можно задать прямую линию в пространстве и другим способом (см. рисунок). Очевидно, что положение любой прямой  однозначно определяется заданием положения какой-либо ее точки однозначно определяется заданием положения какой-либо ее точки 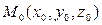 и какого-либо вектора и какого-либо вектора  , параллельного этой прямой (любой такой вектор называется направляющим вектором прямой). Пусть нам даны координаты некоторой точки , параллельного этой прямой (любой такой вектор называется направляющим вектором прямой). Пусть нам даны координаты некоторой точки 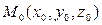 на прямой на прямой  и координаты какого-либо ее направляющего вектора и координаты какого-либо ее направляющего вектора  . Найдем соотношения, которым в этом случае должны удовлетворять координаты . Найдем соотношения, которым в этом случае должны удовлетворять координаты  , ,  и и 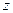 любой точки на этой линии. Пусть любой точки на этой линии. Пусть 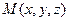 − произвольная точка на линии − произвольная точка на линии  (см. снова рисунок). Рассмотрим вектор (см. снова рисунок). Рассмотрим вектор  . Зная координаты его начальной . Зная координаты его начальной  и конечной и конечной 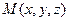 точек, найдем координаты самого вектора (формула (4) в параграфе «Координаты вектора»): точек, найдем координаты самого вектора (формула (4) в параграфе «Координаты вектора»):  . Из приведенного рисунка ясно, что точка . Из приведенного рисунка ясно, что точка 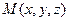 лежит на данной прямой только в том случае, если вектор лежит на данной прямой только в том случае, если вектор  параллелен направляющему вектору параллелен направляющему вектору  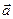 . Выписывая условие параллельности векторов . Выписывая условие параллельности векторов  и и 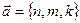 через соотношения их координат (формула (7) в параграфе «Координаты вектора»), получим, что координаты через соотношения их координат (формула (7) в параграфе «Координаты вектора»), получим, что координаты  и и 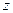 любой точки на прямой любой точки на прямой  удовлетворяют уравнениям удовлетворяют уравнениям
(2) 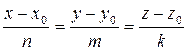 , ,
которые называются каноническими уравнениями прямой. Если прямая задана своими каноническими уравнениями, то она состоит из тех и только из тех точек, координаты  , ,  и и 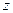 которых удовлетворяют уравнениям (2). которых удовлетворяют уравнениям (2).
Замечание. В канонических уравнениях (2) в знаменателе может оказаться 0, если одна из координат направляющего вектора нулевая. Это не приводит к неприятностям, так как выписанные выше канонические уравнения надо понимать как пропорцию (т.е. равенство 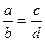 означает, что означает, что 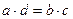 ). Поэтому канонические уравнения прямой (2) корректнее (но менее компактно и удобно) записывать в виде системы ). Поэтому канонические уравнения прямой (2) корректнее (но менее компактно и удобно) записывать в виде системы
(3) 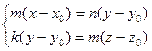 . .
Найдем теперь параметрическое уравнение прямой. Если прямая  задана каноническими уравнениями (2), то для каждой точки задана каноническими уравнениями (2), то для каждой точки 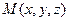 этой прямой выписанные в (2) дроби должны принимать одно и то же числовое значение, которое обозначим через этой прямой выписанные в (2) дроби должны принимать одно и то же числовое значение, которое обозначим через  . Для разных точек на прямой значения . Для разных точек на прямой значения  , конечно, отличаются. Приравнивая каждую дробь в (2) одному и тому же числовому значению , конечно, отличаются. Приравнивая каждую дробь в (2) одному и тому же числовому значению  , получим систему: , получим систему:
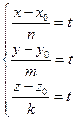 . .
Выражая из этих уравнений координаты текущей точки прямой  и и 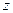 , получим , получим
(4) 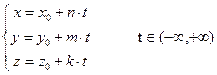
Уравнения этой системы называются параметрическими уравнениями прямой  . Придавая параметру . Придавая параметру  всевозможные числовые значения и подставляя их в параметрические уравнения прямой (4), будем получать координаты всех точек прямой. Например, как легко видеть, при всевозможные числовые значения и подставляя их в параметрические уравнения прямой (4), будем получать координаты всех точек прямой. Например, как легко видеть, при  получим саму точку получим саму точку  , при положительных значениях , при положительных значениях  будем получать точки прямой, расположенные от будем получать точки прямой, расположенные от  по направлению направляющего вектора по направлению направляющего вектора 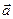 , а при отрицательном , а при отрицательном  − в противоположном направлении. Поэтому каждой точке на прямой соответствует свое значение − в противоположном направлении. Поэтому каждой точке на прямой соответствует свое значение  , при подстановке которого в параметрические уравнения (4) получаются координаты этой точки. , при подстановке которого в параметрические уравнения (4) получаются координаты этой точки.
Итак, мы знаем уже три формы записи уравнений прямой в пространстве: общие уравнения прямой (1), канонические уравнения прямой (2) (или (3)), а также параметрические уравнения (4). В разных задачах удобно использовать разные формы записи уравнения прямой. Может оказаться так, что в условии задачи прямая задана своими уравнениями в одной форме, но для ее решения удобно использовать другую форму уравнений этой прямой. Поэтому нужно уметь переходить от одного вида уравнений прямой к другому ее виду. Переход от параметрических уравнений (4) к каноническим (2) и обратно очевиден, так как обе формы используют одни и те же данные (координаты точки прямой и ее направляющего вектора). Переход от канонических уравнений прямой (2) к общим уравнениям вида (1) был уже проведен выше, когда канонические уравнения (2) были записаны в виде системы (3):
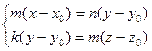 . .
Осталось раскрыть скобки и перенести правую часть в левую.
Пример 1. Даны параметрические уравнения прямой 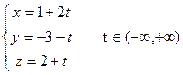 . Найти канонические и общие уравнения этой прямой. . Найти канонические и общие уравнения этой прямой.
Решение. Сравнивая параметрические уравнения данной прямой с общим видом параметрических уравнений (4), сразу получаем координаты точки  , лежащей на прямой, а также координаты ее направляющего вектора , лежащей на прямой, а также координаты ее направляющего вектора 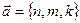 : :  , ,  , ,  ; ; 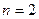 , , 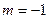 , ,  . По этим данным, глядя на (2), выписываем канонические уравнения прямой: . По этим данным, глядя на (2), выписываем канонические уравнения прямой: 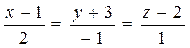 . Теперь из канонических получим общие уравнения прямой. По данной выше рекомендации, нужно сначала канонические уравнения (2) представить в форме (3). Для этого разбиваем полученные канонические уравнения на 2 отдельных равенства и записываем их в систему: . Теперь из канонических получим общие уравнения прямой. По данной выше рекомендации, нужно сначала канонические уравнения (2) представить в форме (3). Для этого разбиваем полученные канонические уравнения на 2 отдельных равенства и записываем их в систему:
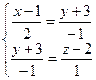    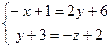   . Для большего эстетического удовлетворения можно (но не обязательно) умножить обе части первого уравнения . Для большего эстетического удовлетворения можно (но не обязательно) умножить обе части первого уравнения  Окончательно, общие уравнения прямой представляются в виде: Окончательно, общие уравнения прямой представляются в виде:  . .
Для перехода от общих уравнений (1) к каноническим уравнениям (2) (или параметрическим (4)) требуется получить из общих уравнений (1) координаты  , , 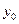 и и 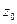 какой-либо точки какой-либо точки  на прямой и координаты на прямой и координаты 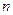 , , 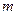 и и  какого-либо ее направляющего вектора какого-либо ее направляющего вектора 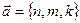 , поскольку знание именно этих величин позволяет записать уравнение прямой как в канонической форме, так и в виде параметрических уравнений. Итак, пусть даны общие уравнения (1) некоторой прямой , поскольку знание именно этих величин позволяет записать уравнение прямой как в канонической форме, так и в виде параметрических уравнений. Итак, пусть даны общие уравнения (1) некоторой прямой  . Нахождение координат . Нахождение координат  , , 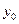 и и 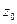 какой-либо точки какой-либо точки  прямой из ее общих уравнений описано выше. Остановимся на выборе направляющего вектора прямой из ее общих уравнений описано выше. Остановимся на выборе направляющего вектора 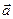 . Из вида уравнений (1) ясно, что данная прямая лежит на пересечении плоскостей . Из вида уравнений (1) ясно, что данная прямая лежит на пересечении плоскостей 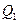 и и 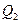 с уравнениями с уравнениями  и и 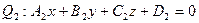 . Обозначим через . Обозначим через 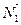 и и  нормальные векторы этих плоскостей, координаты которых, как известно, определяются из уравнений самих плоскостей: нормальные векторы этих плоскостей, координаты которых, как известно, определяются из уравнений самих плоскостей: 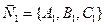 , ,  . Поскольку нормальные векторы . Поскольку нормальные векторы 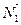 и и  по определению перпендикулярны своим плоскостям по определению перпендикулярны своим плоскостям 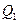 и и 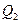 соответственно, а прямая соответственно, а прямая 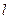 лежит в каждой их этих плоскостей, то прямая лежит в каждой их этих плоскостей, то прямая 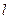 должна быть перпендикулярной каждому из этих векторов. Искомый направляющий вектор должна быть перпендикулярной каждому из этих векторов. Искомый направляющий вектор 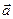 параллелен самой прямой, а потому тоже должен быть перпендикулярным векторам параллелен самой прямой, а потому тоже должен быть перпендикулярным векторам 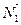 и и  . Итак, искомый направляющий вектор . Итак, искомый направляющий вектор 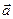 прямой прямой 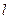 должен быть выбран таким, чтобы он был перпендикулярен каждому нормальному вектору плоскостей должен быть выбран таким, чтобы он был перпендикулярен каждому нормальному вектору плоскостей 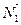 и и  . Один такой вектор мы точно знаем − это векторное произведение векторов . Один такой вектор мы точно знаем − это векторное произведение векторов 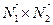 , поскольку по определению при векторном перемножении двух векторов получается вектор, перпендикулярный каждому из этих векторов. Итак, мы выяснили, что в качестве направляющего вектора прямой может быть взят вектор , поскольку по определению при векторном перемножении двух векторов получается вектор, перпендикулярный каждому из этих векторов. Итак, мы выяснили, что в качестве направляющего вектора прямой может быть взят вектор  . .
Пример 2. Даны общие уравнения прямой  . Найти канонические и параметрические уравнения этой прямой. . Найти канонические и параметрические уравнения этой прямой.
Решение. Сначала найдем координаты  , , 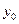 и и 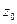 какой-либо точки какой-либо точки  прямой описанным выше способом. Для этого полагаем, например, прямой описанным выше способом. Для этого полагаем, например,  , подставляем в общие уравнения и решаем полученную систему относительно остальных неизвестных , подставляем в общие уравнения и решаем полученную систему относительно остальных неизвестных  и и  : : 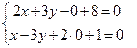  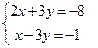 . Выражая из второго уравнения . Выражая из второго уравнения  и подставляя в первое уравнение, получим после его решения и подставляя в первое уравнение, получим после его решения  , а потому , а потому  . Таким образом, . Таким образом,  , ,  , ,  , а потому на прямой лежит точка , а потому на прямой лежит точка  . Найдем по описанному выше алгоритму координаты . Найдем по описанному выше алгоритму координаты 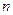 , , 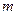 и и  направляющего вектора направляющего вектора 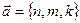 . По виду общих уравнений прямой получаем, что она лежит в пересечении плоскостей . По виду общих уравнений прямой получаем, что она лежит в пересечении плоскостей 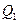 и и 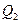 с уравнениями с уравнениями 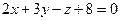 и и 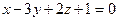 соответственно. По виду уравнений плоскости восстанавливаем координаты их нормальных векторов: соответственно. По виду уравнений плоскости восстанавливаем координаты их нормальных векторов:  , , 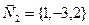 . Как выше обосновано, в качестве направляющего вектора берем их векторное произведение: . Как выше обосновано, в качестве направляющего вектора берем их векторное произведение: 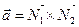 . По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора . По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора 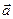 как координаты векторного произведения векторов по координатам самих векторов: как координаты векторного произведения векторов по координатам самих векторов:
 . .
Таким образом, направляющий вектор  , а потому его координаты: , а потому его координаты:  , , 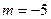 и и 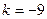 . Теперь найдены все значения параметров, необходимые для написания канонических (2) и параметрических (4) уравнений прямой: . Теперь найдены все значения параметров, необходимые для написания канонических (2) и параметрических (4) уравнений прямой:  , ,  , ,  ; ;  , , 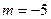 и и 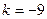 . Подставляя их в (2), получаем канонические уравнения: . Подставляя их в (2), получаем канонические уравнения:  . Подставляя эти параметры в (4), получаем параметрические уравнения прямой: . Подставляя эти параметры в (4), получаем параметрические уравнения прямой: 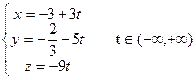 . .
Как известно, положение прямой однозначно определяется положением двух любых ее точек. Поэтому координаты каких-либо двух точек прямой должны однозначно определять вид ее уравнения. Найдем канонические уравнения прямой  , проходящей через две заданные точки , проходящей через две заданные точки 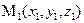 и и 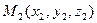 (см. рисунок). Для получения таких уравнений необходимо знать координаты (см. рисунок). Для получения таких уравнений необходимо знать координаты  , , 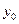 и и 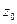 какой-либо точки какой-либо точки  на прямой и координаты на прямой и координаты 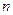 , , 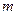 и и  какого-либо ее направляющего вектора какого-либо ее направляющего вектора 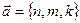 . В качестве известной точки прямой можно взять любую из точек . В качестве известной точки прямой можно взять любую из точек 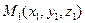 или или 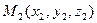 . Возьмем, например, . Возьмем, например, 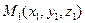 . Осталось найти направляющий вектор, т.е. вектор, параллельный прямой . Осталось найти направляющий вектор, т.е. вектор, параллельный прямой  . .  В качестве такого вектора можно, очевидно, взять вектор В качестве такого вектора можно, очевидно, взять вектор 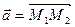 . По известным координатам начальной . По известным координатам начальной 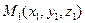 и конечной и конечной 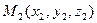 точек этого вектора найдем координаты самого направляющего вектора: точек этого вектора найдем координаты самого направляющего вектора: 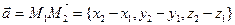 . Зная координаты выбранной точки и координаты направляющего вектора, по формуле (2) легко выписывается каноническое уравнение прямой. Итак, уравнение прямой, проходящей через две заданные точки . Зная координаты выбранной точки и координаты направляющего вектора, по формуле (2) легко выписывается каноническое уравнение прямой. Итак, уравнение прямой, проходящей через две заданные точки 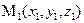 и и 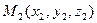 имеет вид: имеет вид:
(5) 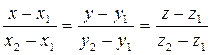 . .
Пример 3. Найти уравнение прямой, проходящей через точки 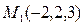 и и 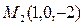 . .
Решение. Подставляя в уравнение (5) заданные координаты точек, получаем:
 или, упрощая, получаем канонические уравнения искомой прямой: или, упрощая, получаем канонические уравнения искомой прямой:  . .
Перейдем теперь к определению взаимного положения прямых по их уравнениям  . Пусть заданы две прямые . Пусть заданы две прямые  и и  с направляющими векторами с направляющими векторами 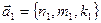 и и 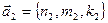 соответственно (см. рисунок). Две прямые в пространстве (в отличие от прямых на плоскости) могут не пересекаться, даже не будучи параллельными друг другу − так называемые скрещивающиеся прямые. Напомним, что угол между двумя данными скрещивающимися прямыми определяется следующим образом. Через произвольную точку пространства проводятся две прямые, параллельные исходным прямым. Тогда угол между ними и будет называться углом между исходными скрещивающимися прямыми. Как и в случае прямых на плоскости будем выбирать острый (или прямой) угол из двух образующихся смежных углов. Из приведенного рисунка видно, что взаимное расположение двух прямых (параллельность, перпендикулярность, величина угла между ними) полностью определяется взаимоположением их направляющих векторов: прямые параллельны (перпендикулярны) только в том случае, когда параллельны (перпендикулярны) их направляющие векторы. Угол между прямыми либо равен углу между их направляющими векторами (если этот угол острый), либо в сумме с ним составляет соответственно (см. рисунок). Две прямые в пространстве (в отличие от прямых на плоскости) могут не пересекаться, даже не будучи параллельными друг другу − так называемые скрещивающиеся прямые. Напомним, что угол между двумя данными скрещивающимися прямыми определяется следующим образом. Через произвольную точку пространства проводятся две прямые, параллельные исходным прямым. Тогда угол между ними и будет называться углом между исходными скрещивающимися прямыми. Как и в случае прямых на плоскости будем выбирать острый (или прямой) угол из двух образующихся смежных углов. Из приведенного рисунка видно, что взаимное расположение двух прямых (параллельность, перпендикулярность, величина угла между ними) полностью определяется взаимоположением их направляющих векторов: прямые параллельны (перпендикулярны) только в том случае, когда параллельны (перпендикулярны) их направляющие векторы. Угол между прямыми либо равен углу между их направляющими векторами (если этот угол острый), либо в сумме с ним составляет 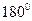 (если угол между направляющими векторами тупой). Поэтому вопрос о параллельности, перпендикулярности или угле между прямыми сводится к вопросу о параллельности, перпендикулярности или угле между их направляющими векторами. Вспоминая полученные ранее критерии параллельности, перпендикулярности и формулу угла между векторами, получим следующие ниже утверждения. Пусть имеются прямые (если угол между направляющими векторами тупой). Поэтому вопрос о параллельности, перпендикулярности или угле между прямыми сводится к вопросу о параллельности, перпендикулярности или угле между их направляющими векторами. Вспоминая полученные ранее критерии параллельности, перпендикулярности и формулу угла между векторами, получим следующие ниже утверждения. Пусть имеются прямые  и и  с направляющими векторами с направляющими векторами 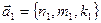 и и 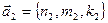 соответственно. Тогда: (6) соответственно. Тогда: (6)  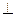    , ,
(7)  || ||   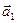 || ||  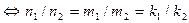 . .
Угол 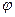 (острый) между прямыми равен (с точностью до смежности, т.е. с точностью до « (острый) между прямыми равен (с точностью до смежности, т.е. с точностью до «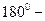 ») углу между направляющими векторами, поэтому ») углу между направляющими векторами, поэтому
(8) 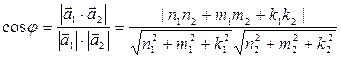 . .
Пример 4. Проверить, будут ли перпендикулярны прямые  и и  , заданные уравнениями , заданные уравнениями 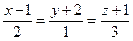 и и  соответственно. соответственно.
Решение. По (6) если прямые  и и  имеют направляющие векторы имеют направляющие векторы 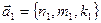 и и 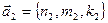 , то , то     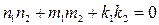 . Поэтому для проверки перпендикулярности прямых необходимо знать координаты их направляющих векторов. Прямая . Поэтому для проверки перпендикулярности прямых необходимо знать координаты их направляющих векторов. Прямая  задана каноническими уравнениями, а потому из вида этого уравнения в соответствии с (2) сразу получаем координаты ее направляющего вектора задана каноническими уравнениями, а потому из вида этого уравнения в соответствии с (2) сразу получаем координаты ее направляющего вектора 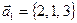 . С прямой . С прямой  сложнее, так как она задана своими общими уравнениями, из вида которых координаты направляющего вектора сразу не извлекаются. Но в примере 2 мы уже для этой прямой строили направляющий вектор, когда хотели из ее общих уравнений получить канонические и параметрические. Воспользовавшись полученным при решении примера 2 результатом, выписываем направляющий вектор прямой сложнее, так как она задана своими общими уравнениями, из вида которых координаты направляющего вектора сразу не извлекаются. Но в примере 2 мы уже для этой прямой строили направляющий вектор, когда хотели из ее общих уравнений получить канонические и параметрические. Воспользовавшись полученным при решении примера 2 результатом, выписываем направляющий вектор прямой  : : 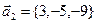 . Теперь, имея координаты направляющих векторов . Теперь, имея координаты направляющих векторов 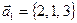 и и 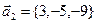 , проверяем условие перпендикулярности (6): , проверяем условие перпендикулярности (6):  . Итак, условие (6) перпендикулярности прямых не выполнено, а потому прямые . Итак, условие (6) перпендикулярности прямых не выполнено, а потому прямые  и и  не перпендикулярны. Каков же все-таки угол между этими прямыми. Выясним это в следующем примере. не перпендикулярны. Каков же все-таки угол между этими прямыми. Выясним это в следующем примере.
Пример 5. Найти угол между прямыми  и и  , заданными уравнениями , заданными уравнениями 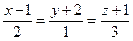 и и  соответственно. соответственно.
Решение. Только что мы выяснили, что эти прямые не перпендикулярны, т.е. угол между ними не равен 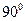 . Для определения угла . Для определения угла 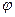 между прямыми воспользуемся найденными в предыдущем примере их направляющими векторами между прямыми воспользуемся найденными в предыдущем примере их направляющими векторами 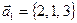 , , 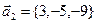 и формулой (8). По этой формуле и формулой (8). По этой формуле  . Поэтому угол . Поэтому угол 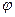 между прямыми таков, что между прямыми таков, что 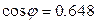 . Для такого угла есть, как известно, специальное обозначение . Для такого угла есть, как известно, специальное обозначение 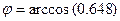 . Воспользовавшись соответствующими таблицами или калькулятором, можно получить . Воспользовавшись соответствующими таблицами или калькулятором, можно получить  . .
Пример 6. Найти уравнение прямой  , проходящей через точку , проходящей через точку  и параллельной прямой и параллельной прямой  с уравнением с уравнением  . .
 Решение. Будем искать канонические уравнения искомой прямой Решение. Будем искать канонические уравнения искомой прямой  , которые по формуле (2) имеют вид: , которые по формуле (2) имеют вид:  . Для написания этих уравнений необходимо знать координаты . Для написания этих уравнений необходимо знать координаты 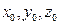 какой-либо точки какой-либо точки  на этой прямой и координаты на этой прямой и координаты  какого-либо ее направляющего вектора какого-либо ее направляющего вектора 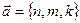 (т.е. вектора, параллельного прямой (т.е. вектора, параллельного прямой  ). Координаты точки, лежащей на ). Координаты точки, лежащей на  , нам заданы в условии, а потому , нам заданы в условии, а потому 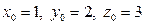 . Поскольку искомая прямая . Поскольку искомая прямая  должна быть параллельной прямой должна быть параллельной прямой  , то направляющий вектор , то направляющий вектор 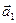 прямой прямой  окажется параллельным и прямой окажется параллельным и прямой  , а потому он может быть взят в качестве направляющего вектора , а потому он может быть взят в качестве направляющего вектора 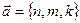 и искомой прямой и искомой прямой  . Итак, наша задача свелась к отысканию координат направляющего вектора прямой . Итак, наша задача свелась к отысканию координат направляющего вектора прямой  , которая задана своими общими уравнениями , которая задана своими общими уравнениями  , т.е. лежит в пересечении плоскостей , т.е. лежит в пересечении плоскостей 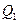 и и 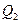 с уравнениями с уравнениями  и и 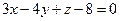 соответственно. По уравнениям плоскостей найдем координаты их нормальных векторов соответственно. По уравнениям плоскостей найдем координаты их нормальных векторов 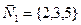 , ,  . Как это было сделано в аналогичной ситуации в примере 2, в качестве направляющего вектора прямой . Как это было сделано в аналогичной ситуации в примере 2, в качестве направляющего вектора прямой  можно взять их векторное произведение: можно взять их векторное произведение: 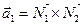 . По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора . По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора 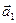 : :
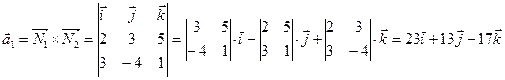 . .
Таким образом, направляющий вектор 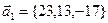 , а потому координаты направляющего вектора искомой прямой: , а потому координаты направляющего вектора искомой прямой:  , ,  и и  . Подставляя найденные параметры в (2), получим канонические уравнения искомой прямой: . Подставляя найденные параметры в (2), получим канонические уравнения искомой прямой:  . .
Взаимное расположение прямой и плоскости в пространстве
Пусть дана плоскость 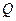 и прямая и прямая  в пространстве. Для определения угла между ними нам понадобится знание координат нормального вектора в пространстве. Для определения угла между ними нам понадобится знание координат нормального вектора  плоскости и направляющего вектора плоскости и направляющего вектора 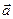 прямой. Напомним, что если плоскость прямой. Напомним, что если плоскость 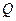 задана, например, своим общим уравнением задана, например, своим общим уравнением  , то координаты нормального вектора есть коэффициенты при , то координаты нормального вектора есть коэффициенты при  , ,  и и 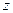 в этом уравнении: в этом уравнении: 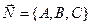 . Что касается направляющего вектора . Что касается направляющего вектора 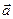 , то если прямая задана каноническими или параметрическими уравнениями, то координаты направляющего вектора непосредственно фигурируют в этих уравнениях на соответствующих местах. Если же прямая задана общими уравнениями, то и для этого случая в предыдущем параграфе обозначена схема поиска координат направляющего вектора (см. пример 2 и текст перед ним). Поэтому будем считать, что и координаты направляющего вектора прямой , то если прямая задана каноническими или параметрическими уравнениями, то координаты направляющего вектора непосредственно фигурируют в этих уравнениях на соответствующих местах. Если же прямая задана общими уравнениями, то и для этого случая в предыдущем параграфе обозначена схема поиска координат направляющего вектора (см. пример 2 и текст перед ним). Поэтому будем считать, что и координаты направляющего вектора прямой 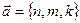 нам тоже в этом случае известны. нам тоже в этом случае известны.
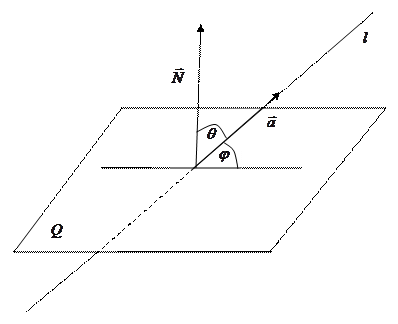 Напомним (из школьного курса), что углом между прямой Напомним (из школьного курса), что углом между прямой  и плоскостью и плоскостью 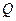 называется угол (снова острый или, в крайнем случае, называется угол (снова острый или, в крайнем случае, 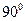 ) между прямой и проекцией этой прямой на плоскость. На рисунке это угол ) между прямой и проекцией этой прямой на плоскость. На рисунке это угол 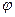 . Кроме того, на рисунке от точки пересечения прямой и плоскости отложен нормальный вектор . Кроме того, на рисунке от точки пересечения прямой и плоскости отложен нормальный вектор 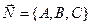 плоскости плоскости 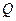 и направляющий вектор и направляющий вектор 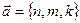 прямой прямой  . Из рисунка видно, что если угол . Из рисунка видно, что если угол 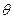 между векторами между векторами 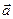 и и  острый, то нужный нам угол острый, то нужный нам угол  . Тогда по формулам приведения . Тогда по формулам приведения  . Но для определения косинуса угла между векторами по координатам самих векторов имеется формула (11) в параграфе «Скалярное произведение векторов». По этой формуле . Но для определения косинуса угла между векторами по координатам самих векторов имеется формула (11) в параграфе «Скалярное произведение векторов». По этой формуле 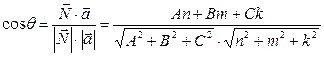 . Таким образом, получаем, что если задана плоскость . Таким образом, получаем, что если задана плоскость 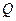 с нормальным вектором с нормальным вектором 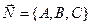 и прямая и прямая  с направляющим вектором с направляющим вектором 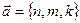 , то синус угла , то синус угла 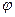 между прямой и плоскостью вычисляется по формуле: между прямой и плоскостью вычисляется по формуле:
(1)  . .
Знак модуля в числителе учитывает и тот случай, когда угол 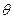 между векторами между векторами 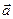 и и  тупой. тупой.
Выведем условия параллельности и перпендикулярности плоскости 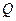 и прямой и прямой  . Из приведенного рисунка видно, что: . Из приведенного рисунка видно, что:
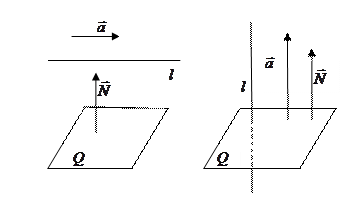 а) прямая и плоскость параллельны тогда и только тогда, когда перпендикулярны нормальный вектор а) прямая и плоскость параллельны тогда и только тогда, когда перпендикулярны нормальный вектор  и направляющий вектор и направляющий вектор 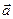 ; б) прямая и плоскость перпендикулярны только тогда, когда параллельны нормальный вектор ; б) прямая и плоскость перпендикулярны только тогда, когда параллельны нормальный вектор  и направляющий вектор и направляющий вектор 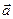 . Используя известные условия параллельности и перпендикулярности векторов (см. формулу (7) параграфа «Свойства координат вектора», а также свойство 5 и формулу (10) параграфа «Скалярное произведение векторов»), получаем следующие критерии параллельности и перпендикулярности прямой и плоскости: . Используя известные условия параллельности и перпендикулярности векторов (см. формулу (7) параграфа «Свойства координат вектора», а также свойство 5 и формулу (10) параграфа «Скалярное произведение векторов»), получаем следующие критерии параллельности и перпендикулярности прямой и плоскости:
(2)  || || 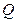  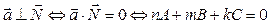 , ,
(3)  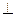 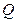  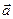 || ||  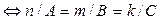 . .
Пример 1. При каком значении р прямая  параллельна плоскости параллельна плоскости  . .
Решение. По критерию (2) данная прямая и плоскость параллельны только в случае выполнения равенства  , т.е. , т.е. 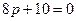 . Отсюда . Отсюда  . .
Пример 2. Найти угол 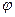 , который составляет прямая , который составляет прямая  с координатной плоскостью с координатной плоскостью  . .
Решение. По формуле (1) для определения угла между прямой и плоскостью нужно знать координаты  какого-либо направляющего вектора прямой какого-либо направляющего вектора прямой 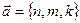 и координаты какого-либо нормального вектора плоскости и координаты какого-либо нормального вектора плоскости 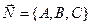 . Как известно, знаменатели канонического уравнения . Как известно, знаменатели канонического уравнения  заданной прямой и образуют координаты ее направляющего вектора. Поэтому в формуле (1) заданной прямой и образуют координаты ее направляющего вектора. Поэтому в формуле (1) 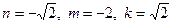 . Найдем координаты какого-либо нормального вектора координатной плоскости . Найдем координаты какого-либо нормального вектора координатной плоскости  , т.е. вектора, ей перпендикулярного. Ясно, что таковым является, например, вектор длины 1, отложенный от начала координат вдоль оси , т.е. вектора, ей перпендикулярного. Ясно, что таковым является, например, вектор длины 1, отложенный от начала координат вдоль оси  . Очевидно, этот вектор имеет координаты . Очевидно, этот вектор имеет координаты 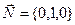 , а потому в формуле (1) можно положить , а потому в формуле (1) можно положить  . Подставляя полученные данные в (1), получаем: . Подставляя полученные данные в (1), получаем:
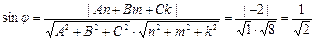 . Такой синус соответствует только одному острому углу, а потому . Такой синус соответствует только одному острому углу, а потому  . .
Пример 3. Найти координаты точки 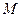 пересечения прямой пересечения прямой  с уравнением с уравнением  и плоскости и плоскости 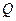 с ура с ура
|



 в пространстве можно задать разными способами (о них шла речь в предыдущем параграфе). Прямая линия может определяться, например, как линия пересечения двух заданных (своими уравнениями) плоскостей
в пространстве можно задать разными способами (о них шла речь в предыдущем параграфе). Прямая линия может определяться, например, как линия пересечения двух заданных (своими уравнениями) плоскостей  и
и 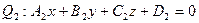 , которые, конечно, не должны быть параллельными. В соответствии с (1) предыдущего параграфа, уравнения этих плоскостей, объединенные в систему, будут называться общими уравнениями прямой
, которые, конечно, не должны быть параллельными. В соответствии с (1) предыдущего параграфа, уравнения этих плоскостей, объединенные в систему, будут называться общими уравнениями прямой 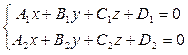 .
. и
и 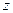 которых удовлетворяют системе (1) (т.е. находятся одновременно на каждой плоскости
которых удовлетворяют системе (1) (т.е. находятся одновременно на каждой плоскости 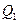 и
и 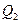 ). Ясно, что одна и та же прямая может быть пересечением многих пар плоскостей. Поэтому общие уравнения прямой определяются самой прямой не однозначно.
). Ясно, что одна и та же прямая может быть пересечением многих пар плоскостей. Поэтому общие уравнения прямой определяются самой прямой не однозначно. и
и  ). Причем, может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.
). Причем, может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты. Можно задать прямую линию в пространстве и другим способом (см. рисунок). Очевидно, что положение любой прямой
Можно задать прямую линию в пространстве и другим способом (см. рисунок). Очевидно, что положение любой прямой 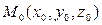 и какого-либо вектора
и какого-либо вектора  , параллельного этой прямой (любой такой вектор называется направляющим вектором прямой). Пусть нам даны координаты некоторой точки
, параллельного этой прямой (любой такой вектор называется направляющим вектором прямой). Пусть нам даны координаты некоторой точки 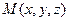 − произвольная точка на линии
− произвольная точка на линии  . Зная координаты его начальной
. Зная координаты его начальной  и конечной
и конечной  . Из приведенного рисунка ясно, что точка
. Из приведенного рисунка ясно, что точка 
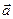 . Выписывая условие параллельности векторов
. Выписывая условие параллельности векторов 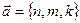 через соотношения их координат (формула (7) в параграфе «Координаты вектора»), получим, что координаты
через соотношения их координат (формула (7) в параграфе «Координаты вектора»), получим, что координаты 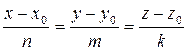 ,
,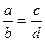 означает, что
означает, что 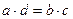 ). Поэтому канонические уравнения прямой (2) корректнее (но менее компактно и удобно) записывать в виде системы
). Поэтому канонические уравнения прямой (2) корректнее (но менее компактно и удобно) записывать в виде системы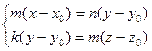 .
. . Для разных точек на прямой значения
. Для разных точек на прямой значения 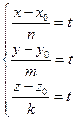 .
.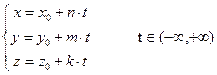
 получим саму точку
получим саму точку  , при положительных значениях
, при положительных значениях 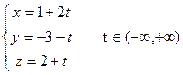 . Найти канонические и общие уравнения этой прямой.
. Найти канонические и общие уравнения этой прямой. ,
,  ,
,  ;
; 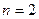 ,
, 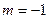 ,
,  . По этим данным, глядя на (2), выписываем канонические уравнения прямой:
. По этим данным, глядя на (2), выписываем канонические уравнения прямой: 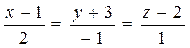 . Теперь из канонических получим общие уравнения прямой. По данной выше рекомендации, нужно сначала канонические уравнения (2) представить в форме (3). Для этого разбиваем полученные канонические уравнения на 2 отдельных равенства и записываем их в систему:
. Теперь из канонических получим общие уравнения прямой. По данной выше рекомендации, нужно сначала канонические уравнения (2) представить в форме (3). Для этого разбиваем полученные канонические уравнения на 2 отдельных равенства и записываем их в систему: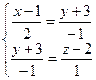


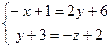
 . Для большего эстетического удовлетворения можно (но не обязательно) умножить обе части первого уравнения
. Для большего эстетического удовлетворения можно (но не обязательно) умножить обе части первого уравнения  Окончательно, общие уравнения прямой представляются в виде:
Окончательно, общие уравнения прямой представляются в виде:  .
. ,
, 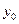 и
и 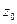 какой-либо точки
какой-либо точки 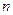 ,
, 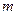 и
и  какого-либо ее направляющего вектора
какого-либо ее направляющего вектора 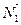 и
и  нормальные векторы этих плоскостей, координаты которых, как известно, определяются из уравнений самих плоскостей:
нормальные векторы этих плоскостей, координаты которых, как известно, определяются из уравнений самих плоскостей: 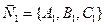 ,
,  . Поскольку нормальные векторы
. Поскольку нормальные векторы 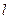 лежит в каждой их этих плоскостей, то прямая
лежит в каждой их этих плоскостей, то прямая 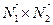 , поскольку по определению при векторном перемножении двух векторов получается вектор, перпендикулярный каждому из этих векторов. Итак, мы выяснили, что в качестве направляющего вектора прямой может быть взят вектор
, поскольку по определению при векторном перемножении двух векторов получается вектор, перпендикулярный каждому из этих векторов. Итак, мы выяснили, что в качестве направляющего вектора прямой может быть взят вектор  .
. . Найти канонические и параметрические уравнения этой прямой.
. Найти канонические и параметрические уравнения этой прямой. , подставляем в общие уравнения и решаем полученную систему относительно остальных неизвестных
, подставляем в общие уравнения и решаем полученную систему относительно остальных неизвестных 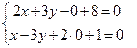
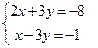 . Выражая из второго уравнения
. Выражая из второго уравнения  и подставляя в первое уравнение, получим после его решения
и подставляя в первое уравнение, получим после его решения  , а потому
, а потому  . Таким образом,
. Таким образом,  ,
,  ,
,  , а потому на прямой лежит точка
, а потому на прямой лежит точка  . Найдем по описанному выше алгоритму координаты
. Найдем по описанному выше алгоритму координаты 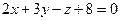 и
и 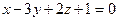 соответственно. По виду уравнений плоскости восстанавливаем координаты их нормальных векторов:
соответственно. По виду уравнений плоскости восстанавливаем координаты их нормальных векторов:  ,
, 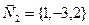 . Как выше обосновано, в качестве направляющего вектора берем их векторное произведение:
. Как выше обосновано, в качестве направляющего вектора берем их векторное произведение: 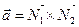 . По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора
. По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора  .
. , а потому его координаты:
, а потому его координаты:  ,
, 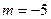 и
и 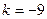 . Теперь найдены все значения параметров, необходимые для написания канонических (2) и параметрических (4) уравнений прямой:
. Теперь найдены все значения параметров, необходимые для написания канонических (2) и параметрических (4) уравнений прямой:  . Подставляя эти параметры в (4), получаем параметрические уравнения прямой:
. Подставляя эти параметры в (4), получаем параметрические уравнения прямой: 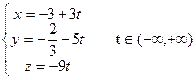 .
.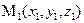 и
и 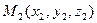 (см. рисунок). Для получения таких уравнений необходимо знать координаты
(см. рисунок). Для получения таких уравнений необходимо знать координаты 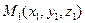 или
или  В качестве такого вектора можно, очевидно, взять вектор
В качестве такого вектора можно, очевидно, взять вектор 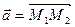 . По известным координатам начальной
. По известным координатам начальной 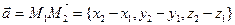 . Зная координаты выбранной точки и координаты направляющего вектора, по формуле (2) легко выписывается каноническое уравнение прямой. Итак, уравнение прямой, проходящей через две заданные точки
. Зная координаты выбранной точки и координаты направляющего вектора, по формуле (2) легко выписывается каноническое уравнение прямой. Итак, уравнение прямой, проходящей через две заданные точки 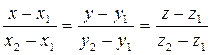 .
.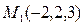 и
и 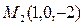 .
. или, упрощая, получаем канонические уравнения искомой прямой:
или, упрощая, получаем канонические уравнения искомой прямой:  .
. . Пусть заданы две прямые
. Пусть заданы две прямые  и
и  с направляющими векторами
с направляющими векторами 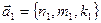 и
и 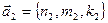 соответственно (см. рисунок). Две прямые в пространстве (в отличие от прямых на плоскости) могут не пересекаться, даже не будучи параллельными друг другу − так называемые скрещивающиеся прямые. Напомним, что угол между двумя данными скрещивающимися прямыми определяется следующим образом. Через произвольную точку пространства проводятся две прямые, параллельные исходным прямым. Тогда угол между ними и будет называться углом между исходными скрещивающимися прямыми. Как и в случае прямых на плоскости будем выбирать острый (или прямой) угол из двух образующихся смежных углов. Из приведенного рисунка видно, что взаимное расположение двух прямых (параллельность, перпендикулярность, величина угла между ними) полностью определяется взаимоположением их направляющих векторов: прямые параллельны (перпендикулярны) только в том случае, когда параллельны (перпендикулярны) их направляющие векторы. Угол между прямыми либо равен углу между их направляющими векторами (если этот угол острый), либо в сумме с ним составляет
соответственно (см. рисунок). Две прямые в пространстве (в отличие от прямых на плоскости) могут не пересекаться, даже не будучи параллельными друг другу − так называемые скрещивающиеся прямые. Напомним, что угол между двумя данными скрещивающимися прямыми определяется следующим образом. Через произвольную точку пространства проводятся две прямые, параллельные исходным прямым. Тогда угол между ними и будет называться углом между исходными скрещивающимися прямыми. Как и в случае прямых на плоскости будем выбирать острый (или прямой) угол из двух образующихся смежных углов. Из приведенного рисунка видно, что взаимное расположение двух прямых (параллельность, перпендикулярность, величина угла между ними) полностью определяется взаимоположением их направляющих векторов: прямые параллельны (перпендикулярны) только в том случае, когда параллельны (перпендикулярны) их направляющие векторы. Угол между прямыми либо равен углу между их направляющими векторами (если этот угол острый), либо в сумме с ним составляет 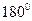 (если угол между направляющими векторами тупой). Поэтому вопрос о параллельности, перпендикулярности или угле между прямыми сводится к вопросу о параллельности, перпендикулярности или угле между их направляющими векторами. Вспоминая полученные ранее критерии параллельности, перпендикулярности и формулу угла между векторами, получим следующие ниже утверждения. Пусть имеются прямые
(если угол между направляющими векторами тупой). Поэтому вопрос о параллельности, перпендикулярности или угле между прямыми сводится к вопросу о параллельности, перпендикулярности или угле между их направляющими векторами. Вспоминая полученные ранее критерии параллельности, перпендикулярности и формулу угла между векторами, получим следующие ниже утверждения. Пусть имеются прямые 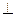
 ,
,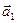 ||
|| 
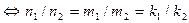 .
.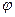 (острый) между прямыми равен (с точностью до смежности, т.е. с точностью до «
(острый) между прямыми равен (с точностью до смежности, т.е. с точностью до «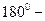 ») углу между направляющими векторами, поэтому
») углу между направляющими векторами, поэтому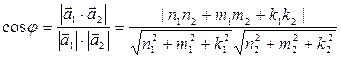 .
.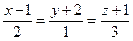 и
и 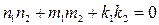 . Поэтому для проверки перпендикулярности прямых необходимо знать координаты их направляющих векторов. Прямая
. Поэтому для проверки перпендикулярности прямых необходимо знать координаты их направляющих векторов. Прямая 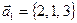 . С прямой
. С прямой 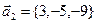 . Теперь, имея координаты направляющих векторов
. Теперь, имея координаты направляющих векторов  . Итак, условие (6) перпендикулярности прямых не выполнено, а потому прямые
. Итак, условие (6) перпендикулярности прямых не выполнено, а потому прямые 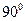 . Для определения угла
. Для определения угла  . Поэтому угол
. Поэтому угол 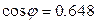 . Для такого угла есть, как известно, специальное обозначение
. Для такого угла есть, как известно, специальное обозначение 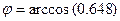 . Воспользовавшись соответствующими таблицами или калькулятором, можно получить
. Воспользовавшись соответствующими таблицами или калькулятором, можно получить  .
. и параллельной прямой
и параллельной прямой  с уравнением
с уравнением  .
. Решение. Будем искать канонические уравнения искомой прямой
Решение. Будем искать канонические уравнения искомой прямой  . Для написания этих уравнений необходимо знать координаты
. Для написания этих уравнений необходимо знать координаты 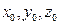 какой-либо точки
какой-либо точки  какого-либо ее направляющего вектора
какого-либо ее направляющего вектора 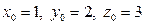 . Поскольку искомая прямая
. Поскольку искомая прямая 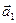 прямой
прямой  , т.е. лежит в пересечении плоскостей
, т.е. лежит в пересечении плоскостей  и
и 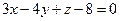 соответственно. По уравнениям плоскостей найдем координаты их нормальных векторов
соответственно. По уравнениям плоскостей найдем координаты их нормальных векторов 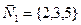 ,
,  . Как это было сделано в аналогичной ситуации в примере 2, в качестве направляющего вектора прямой
. Как это было сделано в аналогичной ситуации в примере 2, в качестве направляющего вектора прямой 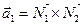 . По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора
. По формуле (14) параграфа «Векторное произведение векторов» находим координаты вектора 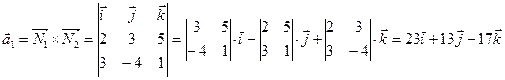 .
.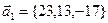 , а потому координаты направляющего вектора искомой прямой:
, а потому координаты направляющего вектора искомой прямой:  ,
,  и
и  . Подставляя найденные параметры в (2), получим канонические уравнения искомой прямой:
. Подставляя найденные параметры в (2), получим канонические уравнения искомой прямой:  .
.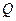 и прямая
и прямая  плоскости и направляющего вектора
плоскости и направляющего вектора  , то координаты нормального вектора есть коэффициенты при
, то координаты нормального вектора есть коэффициенты при 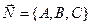 . Что касается направляющего вектора
. Что касается направляющего вектора  Напомним (из школьного курса), что углом между прямой
Напомним (из школьного курса), что углом между прямой 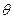 между векторами
между векторами  . Тогда по формулам приведения
. Тогда по формулам приведения  . Но для определения косинуса угла между векторами по координатам самих векторов имеется формула (11) в параграфе «Скалярное произведение векторов». По этой формуле
. Но для определения косинуса угла между векторами по координатам самих векторов имеется формула (11) в параграфе «Скалярное произведение векторов». По этой формуле 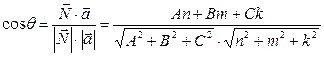 . Таким образом, получаем, что если задана плоскость
. Таким образом, получаем, что если задана плоскость  .
. а) прямая и плоскость параллельны тогда и только тогда, когда перпендикулярны нормальный вектор
а) прямая и плоскость параллельны тогда и только тогда, когда перпендикулярны нормальный вектор 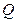
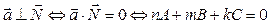 ,
,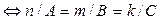 .
. параллельна плоскости
параллельна плоскости  .
. , т.е.
, т.е. 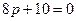 . Отсюда
. Отсюда  .
. с координатной плоскостью
с координатной плоскостью  .
.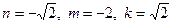 . Найдем координаты какого-либо нормального вектора координатной плоскости
. Найдем координаты какого-либо нормального вектора координатной плоскости 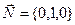 , а потому в формуле (1) можно положить
, а потому в формуле (1) можно положить  . Подставляя полученные данные в (1), получаем:
. Подставляя полученные данные в (1), получаем: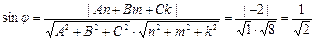 . Такой синус соответствует только одному острому углу, а потому
. Такой синус соответствует только одному острому углу, а потому  .
. пересечения прямой
пересечения прямой  и плоскости
и плоскости 


