

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Уравнение прямой линии на плоскости
Пусть на координатной плоскости хОу находится некоторая прямая  . Найдем вид формул в уравнении (1) для прямой линии. Рассмотрим два случая. . Найдем вид формул в уравнении (1) для прямой линии. Рассмотрим два случая.
 I. Сначала рассмотрим случай, когда прямая I. Сначала рассмотрим случай, когда прямая  не параллельна оси не параллельна оси  (левая часть рисунка). Ясно, что ее уравнение должно содержать параметры, характеризующие положение именно данной прямой. Чем же можно характеризовать положение этой прямой? Поскольку она не параллельна оси (левая часть рисунка). Ясно, что ее уравнение должно содержать параметры, характеризующие положение именно данной прямой. Чем же можно характеризовать положение этой прямой? Поскольку она не параллельна оси  , то она ее пересекает в некоторой точке. Но ось , то она ее пересекает в некоторой точке. Но ось  – числовая ось, поэтому каждой ее точке соответствует некоторое число. Пусть – числовая ось, поэтому каждой ее точке соответствует некоторое число. Пусть  – то число, которое соответствует точке пересечения прямой с осью – то число, которое соответствует точке пересечения прямой с осью  . Достаточно ли задать одно число . Достаточно ли задать одно число  , чтобы однозначно определилось положение прямой? Нет, не достаточно. Через одну точку может проходить бесконечно много прямых. Все они будут отличаться друг от друга углом, который они образуют с осью , чтобы однозначно определилось положение прямой? Нет, не достаточно. Через одну точку может проходить бесконечно много прямых. Все они будут отличаться друг от друга углом, который они образуют с осью 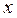 . Вот если кроме числа . Вот если кроме числа  задать и угол задать и угол  , под которым прямая пересекает ось , под которым прямая пересекает ось 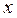 , то положение прямой определится однозначно, а значит эти два параметра должны определять уравнение данной прямой. Действительно, несложно показать, что уравнение прямой l может быть записано в виде , то положение прямой определится однозначно, а значит эти два параметра должны определять уравнение данной прямой. Действительно, несложно показать, что уравнение прямой l может быть записано в виде
(2)  , ,
где число  называется угловым коэффициентом прямой l, а само уравнение (2) называется у равнением прямой с угловым коэффициентом. Итак, уравнение любой прямой, не параллельной оси называется угловым коэффициентом прямой l, а само уравнение (2) называется у равнением прямой с угловым коэффициентом. Итак, уравнение любой прямой, не параллельной оси  , может быть записано в виде уравнения с угловым коэффициентом (2), где угловой коэффициент , может быть записано в виде уравнения с угловым коэффициентом (2), где угловой коэффициент  , ,  − угол, под которым прямая пересекает ось − угол, под которым прямая пересекает ось 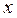 (угол откладывается от оси (угол откладывается от оси 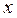 против часовой стрелки), а против часовой стрелки), а  − ордината точки пересечения прямой с осью − ордината точки пересечения прямой с осью  . Если сравнить уравнение (2) с общим уравнением кривой (1), то видно, что для прямых линий формула . Если сравнить уравнение (2) с общим уравнением кривой (1), то видно, что для прямых линий формула  имеет совсем простой вид имеет совсем простой вид
 , а формула , а формула 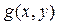 − тоже простого вида: − тоже простого вида:  . .
Пример 1. Найти уравнение прямой, которая пересекает ось  в точке, соответствующей числу 3, и пересекает ось в точке, соответствующей числу 3, и пересекает ось  под углом под углом  . .
Решение. Уравнение прямой имеет вид  . По условию задачи . По условию задачи  , а , а  . Поэтому угловой коэффициент . Поэтому угловой коэффициент  . Подставляя, получим уравнение прямой . Подставляя, получим уравнение прямой 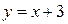 . .
При любых значениях параметров  и и  уравнение (2) является уравнением некоторой прямой на плоскости. Если мы в уравнении (2) заставим параметры уравнение (2) является уравнением некоторой прямой на плоскости. Если мы в уравнении (2) заставим параметры  и и  пробегать всевозможные числовые значения, то в результате получим уравнения всех прямых на плоскости (не параллельных оси у, конечно). Рассмотрим положение таких прямых, когда один из этих параметров равен нулю. Пусть пробегать всевозможные числовые значения, то в результате получим уравнения всех прямых на плоскости (не параллельных оси у, конечно). Рассмотрим положение таких прямых, когда один из этих параметров равен нулю. Пусть  , а потому уравнение соответствующей прямой имеет вид , а потому уравнение соответствующей прямой имеет вид  , где , где 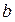 − некоторое число. В этом случае − некоторое число. В этом случае  , а отсюда следует (если вспомнить значения тангенса), что , а отсюда следует (если вспомнить значения тангенса), что  . Отсюда следует, что прямая с та . Отсюда следует, что прямая с та  ким уравнением составляет с осью ким уравнением составляет с осью 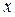 нулевой угол. Нулевой угол составляют между собой только параллельные либо совпадающие прямые. Поэтому уравнение нулевой угол. Нулевой угол составляют между собой только параллельные либо совпадающие прямые. Поэтому уравнение  представляет собой уравнение прямой, параллельной оси представляет собой уравнение прямой, параллельной оси 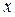 и проходящей через число и проходящей через число 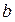 на оси у (см. рисунок). В частности, уравнение на оси у (см. рисунок). В частности, уравнение  (т.е. когда (т.е. когда  ) есть уравнение прямой, совпадающей с осью ) есть уравнение прямой, совпадающей с осью 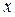 . Пусть теперь в уравнении прямой с угловым коэффициентом (2) параметр . Пусть теперь в уравнении прямой с угловым коэффициентом (2) параметр  , а потому уравнение прямой имеет вид , а потому уравнение прямой имеет вид  (например, (например,  или или 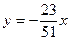 ). То, что ). То, что 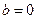 , означает, что прямая пересекает ось , означает, что прямая пересекает ось 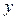 в начале координат. Таким образом, уравнение вида в начале координат. Таким образом, уравнение вида  есть уравнение прямой, проходящей через начало координат (см. рисунок). есть уравнение прямой, проходящей через начало координат (см. рисунок).
II. Теперь рассмотрим случай, когда прямая  параллельна оси параллельна оси  (правая часть предыдущего рисунка). В этом случае уравнение такой прямой не может быть записано в виде уравнения (2) с угловым коэффициентом (правая часть предыдущего рисунка). В этом случае уравнение такой прямой не может быть записано в виде уравнения (2) с угловым коэффициентом  . Действительно, если прямая параллельна оси у, то числа . Действительно, если прямая параллельна оси у, то числа  и и  не существуют в том смысле, как мы раньше их определили. Числа не существуют в том смысле, как мы раньше их определили. Числа  нет, так как прямая вообще ось у не пересекает, а угловой коэффициент нет, так как прямая вообще ось у не пересекает, а угловой коэффициент  не существует потому, что в этом случае не существует потому, что в этом случае 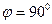 , а , а 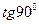 , как известно, не определен. Как же записать уравнение такой прямой? Все же ось , как известно, не определен. Как же записать уравнение такой прямой? Все же ось 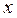 такая прямая обязана пересечь в какой-либо точке. Пусть эта точка на оси такая прямая обязана пересечь в какой-либо точке. Пусть эта точка на оси 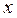 соответствует некоторому числу соответствует некоторому числу  . Вспомним, что уравнение любой линии это (по определению) соотношение, которому должны удовлетворять координаты . Вспомним, что уравнение любой линии это (по определению) соотношение, которому должны удовлетворять координаты  любой точки этой линии. Глядя на рисунок, изображающий обсуждаемую прямую, легко понять, что все точки прямой подчинены единственному требованию: их любой точки этой линии. Глядя на рисунок, изображающий обсуждаемую прямую, легко понять, что все точки прямой подчинены единственному требованию: их 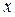 - координата (она же абсцисса) должна быть равной числу - координата (она же абсцисса) должна быть равной числу  . А потому уравнением данной прямой надо признать соотношение . А потому уравнением данной прямой надо признать соотношение  . Таким образом, уравнение любой прямой, параллельной оси у, имеет вид . Таким образом, уравнение любой прямой, параллельной оси у, имеет вид
(3)  , ,
где  − число, в котором прямая пересекает ось − число, в котором прямая пересекает ось 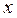 . В частности, если . В частности, если 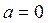 , то прямая совпадет с осью у. Поэтому , то прямая совпадет с осью у. Поэтому  есть уравнение прямой, совпадающей с осью есть уравнение прямой, совпадающей с осью 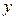 . .
Уравнение прямой линии (да и любой другой линии) играет для этой линии ту же роль, что координаты для вектора. Это уравнение позволяет однозначно представить положение линии на плоскости, описать ее положение относительно других линий, найти точки пересечения с другими линиями, найти углы, образованные линиями и т.д.. Соответствующие формулы будут нами далее пройдены. Однако на пути получения таких формул есть одно неудобство. Связано оно с тем, что разные типы прямых (параллельные оси у и не параллельные) описываются разными уравнениями (2) и (3). Поэтому при получении формул, скажем, для угла между двумя прямыми пришлось бы рассматривать разные случаи положения самих прямых и пользоваться каждый раз разными их уравнениями. Поэтому возникает вопрос: нельзя ли найти такую единую форму уравнения, в которой можно было бы записать уравнение любой прямой − параллельной оси у и не параллельной? Как обычно, ответ − можно. Оказывается, что уравнение любой прямой может быть записано в виде:
(4) 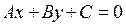 , ,
где 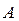 , , 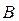 и и  − некоторые числа (для разных прямых − разные). Уравнение вида (4) называется общим уравнением прямой. Меняя всевозможным образом числа − некоторые числа (для разных прямых − разные). Уравнение вида (4) называется общим уравнением прямой. Меняя всевозможным образом числа 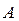 , , 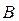 и и  ив (4), получим уравнение всех прямых на плоскости. Для доказательства того, что в форме (4) может быть представлено уравнение любой прямой, достаточно в уравнениях (2) и (3) перенести все в левую часть – сразу определятся нужные значения ив (4), получим уравнение всех прямых на плоскости. Для доказательства того, что в форме (4) может быть представлено уравнение любой прямой, достаточно в уравнениях (2) и (3) перенести все в левую часть – сразу определятся нужные значения 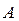 , , 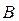 и и  . Преимущество общего уравнения прямой (4) состоит в том, что в таком едином виде можно записать уравнение любой прямой. Недостатком этого уравнения следует считать то, что оно содержит 3 параметра ( . Преимущество общего уравнения прямой (4) состоит в том, что в таком едином виде можно записать уравнение любой прямой. Недостатком этого уравнения следует считать то, что оно содержит 3 параметра (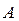 , , 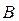 и и  ), в то время как уравнение (2) содержит 2 параметра ( ), в то время как уравнение (2) содержит 2 параметра ( и и  ), а уравнение (3) – один параметр ), а уравнение (3) – один параметр  для нахождения уравнения прямой. Поэтому, если в задаче на нахождение по некоторым данным уравнения прямой известно, что она параллельна либо не параллельна оси у, то чаще предпочтительнее это уравнение искать в виде (3) или (2) соответственно. для нахождения уравнения прямой. Поэтому, если в задаче на нахождение по некоторым данным уравнения прямой известно, что она параллельна либо не параллельна оси у, то чаще предпочтительнее это уравнение искать в виде (3) или (2) соответственно.
Как выше было сказано, с помощью уравнений прямых можно определить их положение на плоскости и характеристики их взаимного расположения. Начнем с нахождения положения (т.е. координат) точки пересечения двух прямых с известными уравнениями.
 Даны уравнения (общие) двух прямых Даны уравнения (общие) двух прямых  и и  . Требуется (не строя их) найти координаты точки их пересечения М (см. рисунок). Поскольку эта точка лежит на прямой . Требуется (не строя их) найти координаты точки их пересечения М (см. рисунок). Поскольку эта точка лежит на прямой  , то ее координаты , то ее координаты  и и 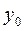 должны удовлетворять уравнению этой прямой, т.е. должно выполняться равенство: должны удовлетворять уравнению этой прямой, т.е. должно выполняться равенство:  . По аналогичным соображениям числа . По аналогичным соображениям числа  и и 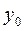 должны удовлетворять и уравнению второй прямой: должны удовлетворять и уравнению второй прямой: 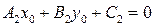 . Таким образом, координаты . Таким образом, координаты  и и 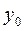 точки их пересечения точки их пересечения 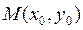 удовлетворяют системе уравнений удовлетворяют системе уравнений
(5) 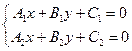 . .
Вывод: Координаты точки пересечения прямых с уравнениями  и и  есть решение системы уравнений (5). есть решение системы уравнений (5).
Пример 2. Найти координаты точки пересечения прямых, заданных уравнениями  и и  . .
Решение. Согласно (5), объединяем уравнения этих прямых в систему
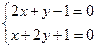 и решаем ее. Если числа в уравнениях системы перенести в правую часть, получим типичный вид системы двух линейных уравнений с двумя неизвестными. Хотя ранее мы проходили серьезные методы решения подобных систем, данную системы решим «школьными» методами, выражая из одного уравнения одну неизвестную через другую и подставляя в оставшееся уравнение. Из первого уравнения и решаем ее. Если числа в уравнениях системы перенести в правую часть, получим типичный вид системы двух линейных уравнений с двумя неизвестными. Хотя ранее мы проходили серьезные методы решения подобных систем, данную системы решим «школьными» методами, выражая из одного уравнения одну неизвестную через другую и подставляя в оставшееся уравнение. Из первого уравнения 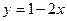 , подставляя во второе уравнение , подставляя во второе уравнение  и решая, получим и решая, получим 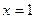 , а потому , а потому  . Итак, прямые пересекаются в точке . Итак, прямые пересекаются в точке  . .
Научимся теперь строить прямые по заданному их уравнению. 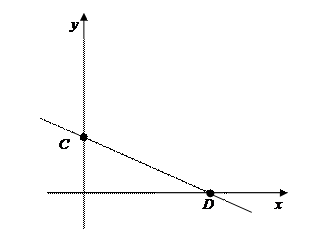 Пусть уравнение прямой имеет вид Пусть уравнение прямой имеет вид  (уравнение любой прямой можно представить в таком виде). Требуется построить эту прямую. Построение прямых линий облегчается тем, что надо узнать положение лишь двух любых ее точек (через любые две точки проходит единственная прямая). Положение каждой точки определяется двумя координатами. Таким образом, по уравнению прямой надо найти 4 неизвестных числа – по две координаты каждой точки. Воспользуемся тем, что эта пара точек может быть любой, и будем искать те точки прямой, для определения положения которых неизвестных надо будет находить меньше. Такими точками являются точки пересечения прямой с осями координат (точки C и D на рисунке). Значение одной из координат этих точек известно заранее, так как точки лежат на осях координат. Ясно, что точка С имеет нулевую первую координату, а точка D − вторую. Поэтому для определения положения точек С и D надо будет найти только 2 числа − их оставшиеся координаты. Найдем координаты точки С. Эта точка является точкой пересечения данной прямой и прямой, совпадающей с осью у. По выше выведенному правилу для получения координат точки С надо решить систему (5), состоящую из уравнения данной прямой и уравнения прямой, совпадающей с осью у. Ранее мы получали уравнение такой прямой: (уравнение любой прямой можно представить в таком виде). Требуется построить эту прямую. Построение прямых линий облегчается тем, что надо узнать положение лишь двух любых ее точек (через любые две точки проходит единственная прямая). Положение каждой точки определяется двумя координатами. Таким образом, по уравнению прямой надо найти 4 неизвестных числа – по две координаты каждой точки. Воспользуемся тем, что эта пара точек может быть любой, и будем искать те точки прямой, для определения положения которых неизвестных надо будет находить меньше. Такими точками являются точки пересечения прямой с осями координат (точки C и D на рисунке). Значение одной из координат этих точек известно заранее, так как точки лежат на осях координат. Ясно, что точка С имеет нулевую первую координату, а точка D − вторую. Поэтому для определения положения точек С и D надо будет найти только 2 числа − их оставшиеся координаты. Найдем координаты точки С. Эта точка является точкой пересечения данной прямой и прямой, совпадающей с осью у. По выше выведенному правилу для получения координат точки С надо решить систему (5), состоящую из уравнения данной прямой и уравнения прямой, совпадающей с осью у. Ранее мы получали уравнение такой прямой: 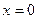 . Поэтому координаты точки С можно найти из системы: . Поэтому координаты точки С можно найти из системы:  . Аналогичные рассуждения приводят к выводу, что координаты точки D можно найти из системы: . Аналогичные рассуждения приводят к выводу, что координаты точки D можно найти из системы:  . Решив эти системы, определим положение точек С и D на осях координат, а затем через эти точки проведем прямую, которая и будет искомой. . Решив эти системы, определим положение точек С и D на осях координат, а затем через эти точки проведем прямую, которая и будет искомой.
Пример 3. Построить прямую с уравнением  . .
 Решение. По полученному правилу координаты точки С пересечения этой прямой с осью у определяются решением системы уравнений Решение. По полученному правилу координаты точки С пересечения этой прямой с осью у определяются решением системы уравнений  . Ее решение: x=0, y=2, а потому С(0, 2). Координаты точки D пересечения этой прямой с осью х определяются решением системы уравнений . Ее решение: x=0, y=2, а потому С(0, 2). Координаты точки D пересечения этой прямой с осью х определяются решением системы уравнений  . Ее решение: . Ее решение:  , ,  , а потому , а потому  . Осталось отметить на координатной плоскости эти точки с известными координатами и провести через них прямую (на рисунке). . Осталось отметить на координатной плоскости эти точки с известными координатами и провести через них прямую (на рисунке).
Перейдем теперь к вопросу определения угла между прямыми по уравнениям прямых. Поскольку при пересечении прямые образуют между собой два угла (один острый, другой тупой, в сумме дают  ), то договоримся, какой из них будем считать углом между прямыми. Углом между прямыми называется острый (или прямой) угол из двух смежных углов, образуемых при пересечении этих прямых (если прямые параллельны, то угол между ними считается равным нулю). На рисунке (выше, который иллюстрировал точку пересечения прямых) это угол обозначен буквой ), то договоримся, какой из них будем считать углом между прямыми. Углом между прямыми называется острый (или прямой) угол из двух смежных углов, образуемых при пересечении этих прямых (если прямые параллельны, то угол между ними считается равным нулю). На рисунке (выше, который иллюстрировал точку пересечения прямых) это угол обозначен буквой  . Если уравнения прямых имеют вид уравнений с угловыми коэффициентами . Если уравнения прямых имеют вид уравнений с угловыми коэффициентами 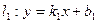 , , 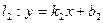 , то можно вывести формулу для тангенса угла между прямыми: , то можно вывести формулу для тангенса угла между прямыми:
(6)  , ,  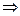  . .
Если же прямые заданы своими общими уравнениями  и и  то формула выглядит так: то формула выглядит так:
(7)  , ,  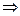  . .
Знак модуля в формулах (6) и (7) поставлен для того, чтобы значения тангенса оказывались бы положительными, что соответствует именно острому углу  . .
Пример 4. Найти угол  между прямыми между прямыми  и и  , заданными уравнениями , заданными уравнениями  и и  . .
Решение. Прямая  задана своим общим уравнением, прямая задана своим общим уравнением, прямая  − уравнением с угловым коэффициентом. Однако, как формула (6), так и формула (7) требуют однотипных уравнений для прямых. Поэтому есть два пути − либо общее уравнение для прямой − уравнением с угловым коэффициентом. Однако, как формула (6), так и формула (7) требуют однотипных уравнений для прямых. Поэтому есть два пути − либо общее уравнение для прямой  привести к уравнению с угловым коэффициентом и воспользоваться формулой (6), либо уравнение с угловым коэффициентом для привести к уравнению с угловым коэффициентом и воспользоваться формулой (6), либо уравнение с угловым коэффициентом для  привести к общему уравнению и воспользоваться формулой (7). Попробуем реализовать оба пути (и убедимся, что результаты совпадут). привести к общему уравнению и воспользоваться формулой (7). Попробуем реализовать оба пути (и убедимся, что результаты совпадут).
1) Выражая 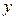 из уравнения прямой из уравнения прямой  , получим уравнение с угловым коэффициентом в виде , получим уравнение с угловым коэффициентом в виде  . Поэтому угловой коэффициент первой прямой . Поэтому угловой коэффициент первой прямой 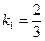 . Из уравнения второй прямой видно, что ее угловой коэффициент . Из уравнения второй прямой видно, что ее угловой коэффициент  . По формуле (6) получаем . По формуле (6) получаем  . Вспоминая значения тангенса известных углов, получаем, что угол меду прямыми . Вспоминая значения тангенса известных углов, получаем, что угол меду прямыми  . .
2) Перенося в заданном уравнении второй прямой все в левую часть, получим общее уравнение второй прямой в виде  . Поэтому для применения формулы (7) получаем такие значения параметров: . Поэтому для применения формулы (7) получаем такие значения параметров:  , , 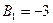 , ,  , ,  . Подставляя их в формулу (7), получаем . Подставляя их в формулу (7), получаем  . Вывод тот же: . Вывод тот же:  . .
Зная формулы (6) и (7) для определения угла между прямыми, можно вывести условия, при которых по этим формулам получается  или или 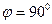 , что соответствует параллельности или перпендикулярности прямых. Выведем условия параллельности и перпендикулярности прямых, заданных, например, уравнениями с угловым коэффициентом. Пусть даны прямые с уравнениями , что соответствует параллельности или перпендикулярности прямых. Выведем условия параллельности и перпендикулярности прямых, заданных, например, уравнениями с угловым коэффициентом. Пусть даны прямые с уравнениями 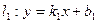 , , 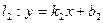 . Пусть . Пусть  , тогда угол между ними , тогда угол между ними  , а потому и , а потому и  . Но по формуле (6): . Но по формуле (6): 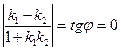 , поэтому , поэтому  . Дробь равна нулю, если ее числитель равен нулю, а потому . Дробь равна нулю, если ее числитель равен нулю, а потому 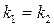 . Итак, параллельность прямых равносильна равенству их угловых коэффициентов. Выведем теперь условие перпендикулярности прямых с уравнениями . Итак, параллельность прямых равносильна равенству их угловых коэффициентов. Выведем теперь условие перпендикулярности прямых с уравнениями 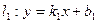 , , 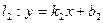 . Если . Если  , то угол между ними , то угол между ними 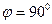 . Но . Но  не существует (тангенс равен синус делить на косинус, а не существует (тангенс равен синус делить на косинус, а  , но на 0 делить нельзя). Поскольку по формуле (6): , но на 0 делить нельзя). Поскольку по формуле (6):  , то дробь , то дробь  тоже не должна существовать. Дробь не существует только в том случае, когда ее знаменатель равен 0. Поэтому тоже не должна существовать. Дробь не существует только в том случае, когда ее знаменатель равен 0. Поэтому 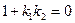 , а потому , а потому  . Таким образом перпендикулярность прямых равносильна тому, что их угловые коэффициенты в произведении дают . Таким образом перпендикулярность прямых равносильна тому, что их угловые коэффициенты в произведении дают  . Аналогично выводятся условия параллельности и перпендикулярности прямых, заданных своими общими уравнениями с использованием формулы (7). . Аналогично выводятся условия параллельности и перпендикулярности прямых, заданных своими общими уравнениями с использованием формулы (7).
В результате приведенных рассуждений получаются следующие условия параллельности и перпендикулярности прямых, заданных либо уравнениями с угловым коэффициентом, либо общими уравнениями. Если прямые заданы уравнениями с угловым коэффициентом, то
(8)  , ,  : :  , ,  . .
Если же прямые заданы общими уравнениями, то
(9)  , ,  : : 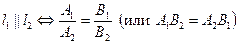 , ,
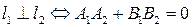 . .
Условие  вместо вместо 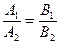 в (9) удобнее применять, если одно из чисел в (9) удобнее применять, если одно из чисел 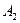 или или  в знаменателях обращается в 0. в знаменателях обращается в 0.
Пример 5. При каком значении 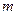 прямые прямые  и и  параллельны, а при каком перпендикулярны. параллельны, а при каком перпендикулярны.
Решение. Для единообразия запишем уравнение второй прямой в общем виде:  . Поскольку теперь обе прямые заданы своими общими уравнениями, то используем критерий (9). По этому критерию прямые с уравнениями . Поскольку теперь обе прямые заданы своими общими уравнениями, то используем критерий (9). По этому критерию прямые с уравнениями  и и  параллельны, если выполнено параллельны, если выполнено  , т.е. при , т.е. при 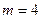 . По этому же критерию (9) прямые перпендикулярны, если . По этому же критерию (9) прямые перпендикулярны, если  , т.е. при , т.е. при 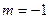 . .
Пример 6. Найти уравнение прямой, проходящей через точку  и перпендикулярную прямой и перпендикулярную прямой  . .
Решение. Для удобства обозначим искомую прямую через  , а ей перпендикулярную прямую с уравнением , а ей перпендикулярную прямую с уравнением  через через  . Будем искать уравнение искомой прямой . Будем искать уравнение искомой прямой  в виде уравнения с угловым коэффициентом в виде уравнения с угловым коэффициентом  . Осталось найти числа . Осталось найти числа  и и  . Поскольку искомая прямая . Поскольку искомая прямая  должна быть перпендикулярна должна быть перпендикулярна  , то по (8) их угловые коэффициенты при перемножении должны давать , то по (8) их угловые коэффициенты при перемножении должны давать  . Угловые коэффициенты этих прямых − это коэффициенты при . Угловые коэффициенты этих прямых − это коэффициенты при  в их уравнениях. Поэтому для перпендикулярности прямых должно выполняться условие: в их уравнениях. Поэтому для перпендикулярности прямых должно выполняться условие:  , откуда , откуда  (отметим, что если бы в задаче надо было бы строить уравнение прямой (отметим, что если бы в задаче надо было бы строить уравнение прямой  , параллельной , параллельной  , то по (8) мы получили бы , то по (8) мы получили бы  ). Таким образом, уравнение прямой ). Таким образом, уравнение прямой  имеет вид имеет вид  , осталось найти число , осталось найти число  . Для его поиска используем тот факт, что точка . Для его поиска используем тот факт, что точка  должна лежать на должна лежать на  , а значит, ее координаты должны удовлетворять уравнению , а значит, ее координаты должны удовлетворять уравнению  этой прямой. Подставив координаты этой точки этой прямой. Подставив координаты этой точки 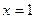 и и 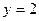 в уравнение прямой, получим в уравнение прямой, получим  , откуда , откуда 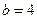 . Подставляя найденное . Подставляя найденное   , получим уравнение искомой прямой , получим уравнение искомой прямой  . .
 При решении задач часто возникает необходимость найти уравнение прямой, если известно положение (т.е. координаты) двух ее точек. Поскольку через любые 2 точки проходит единственная прямая, то положение двух точек должно полностью определять положение всей прямой, а потому и ее уравнение. Пусть известны двух точек При решении задач часто возникает необходимость найти уравнение прямой, если известно положение (т.е. координаты) двух ее точек. Поскольку через любые 2 точки проходит единственная прямая, то положение двух точек должно полностью определять положение всей прямой, а потому и ее уравнение. Пусть известны двух точек  и и  некоторой прямой некоторой прямой  (см. рисунок). Тогда уравнение этой прямой может быть записано в виде (см. рисунок). Тогда уравнение этой прямой может быть записано в виде
(10)  . .
Если при решении конкретной задачи в знаменателях дробей в (10) возникают нули, то равенство следует понимать как пропорцию, т.е. должно выполняться  . Формулу (10) можно получить, если подставить в уравнение прямой . Формулу (10) можно получить, если подставить в уравнение прямой 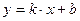 поочередно координаты обеих точек и решить полученную систему относительно параметров поочередно координаты обеих точек и решить полученную систему относительно параметров  и и  . Формула (10)представляет собой наиболее компактную и запоминающуюся запись уравнения прямой, проходящей через две заданные точки . Формула (10)представляет собой наиболее компактную и запоминающуюся запись уравнения прямой, проходящей через две заданные точки  и и  . От уравнения в этой форме легко перейти к традиционной форме уравнения прямой (общее уравнение или уравнение с угловым коэффициентом). . От уравнения в этой форме легко перейти к традиционной форме уравнения прямой (общее уравнение или уравнение с угловым коэффициентом).
Пример 7. Найти уравнение прямой  , проходящей через точки , проходящей через точки  и и  . .
Решение. Из условия задачи получаем следующие значения параметров для подстановки их в формулу (10):  , ,  , , 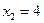 , , 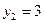 . Подставляя их в (10), получаем уравнение прямой . Подставляя их в (10), получаем уравнение прямой 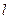 : : 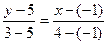 или или  . Поэтому . Поэтому  , а после раскрытия скобок , а после раскрытия скобок  . Перенося теперь все в левую часть, получим общее уравнение искомой прямой . Перенося теперь все в левую часть, получим общее уравнение искомой прямой 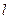 : :  . .
Пример 8. Найти уравнение прямой  , проходящей через точку , проходящей через точку   и точку пересечения прямых и точку пересечения прямых  и и  с уравнениями с уравнениями  и и  . .
 Решение. На рисунке схематически изображены данные задачи и искомая прямая Решение. На рисунке схематически изображены данные задачи и искомая прямая  . Координаты одной из точек прямой . Координаты одной из точек прямой  (точки (точки 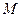 ) известны по условию. Осталось найти координаты какой-нибудь другой ее точки, чтобы можно было бы воспользоваться (10). По условию прямая ) известны по условию. Осталось найти координаты какой-нибудь другой ее точки, чтобы можно было бы воспользоваться (10). По условию прямая 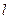 должна проходить через еще одну точку должна проходить через еще одну точку  точку пересечения прямых точку пересечения прямых  и и  . Найдем ее координаты. Выше, в примере 2, мы уже находили координаты точки пересечения этих прямых, записывая уравнения этих прямых в систему и решая ее. Воспользовавшись результатами решения этого примера, выписываем координаты точки . Найдем ее координаты. Выше, в примере 2, мы уже находили координаты точки пересечения этих прямых, записывая уравнения этих прямых в систему и решая ее. Воспользовавшись результатами решения этого примера, выписываем координаты точки  : :  . Таким образом, необходимо найти уравнение прямой . Таким образом, необходимо найти уравнение прямой  , проходящей через точки , проходящей через точки  и и  . Для использования формулы (10) условно принимаем точку . Для использования формулы (10) условно принимаем точку  за первую точку, а за первую точку, а  за вторую. Тогда значения параметров в формуле (10) такие: за вторую. Тогда значения параметров в формуле (10) такие:  , , 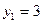 , , 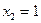 , ,  . Подставляя их в (10), получаем уравнение прямой . Подставляя их в (10), получаем уравнение прямой 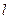 : : 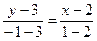 или или  . Умножая обе части на . Умножая обе части на  , получим , получим  . Перенося теперь тройку из левой части в правую, получим уравнение искомой прямой . Перенося теперь тройку из левой части в правую, получим уравнение искомой прямой 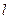 в форме уравнения с угловым коэффициентом: в форме уравнения с угловым коэффициентом: 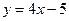 . .
Напоследок приведем формулу, выражающую расстояние от точки до прямой, если известны положение (т.е. координаты) точки и уравнение прямой. Эта формула часто применяется при решении геометрических задач. Расстояние от точки до прямой есть длина перпендикуляра, проведенного из точки на прямую (см. рисунок). Если даны координаты точки 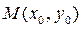 и общее уравнение прямой и общее уравнение прямой  : :  , то искомое расстояние вычисляется по формуле: , то искомое расстояние вычисляется по формуле:
(11) 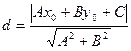 . .
Если уравнение прямой  дано не в форме общего уравнения прямой, а, скажем, уравнения с угловым коэффициентом, то для применения формулы (11) следует привести уравнение к виду общего уравнения. дано не в форме общего уравнения прямой, а, скажем, уравнения с угловым коэффициентом, то для применения формулы (11) следует привести уравнение к виду общего уравнения.
Пример 9. Найти расстояние от точки  до прямой с уравнением до прямой с уравнением  . .
Решение. Перенеся все в левую часть, получим уравнение прямой в форме общего уравнения:  . По формуле (11) получаем, что искомое расстояние . По формуле (11) получаем, что искомое расстояние  . .
Пример 10. Даны координаты вершин   : :  , ,  , ,  . Найти длину высоты из вершины А. . Найти длину высоты из вершины А.
Указание. Сначала по формуле (10) найти уравнение прямой ВС по известным координатам точек В и С. Затем по формуле (11) найти расстояние от точки А до прямой ВС. Это и есть длина высоты.
Кривые второго порядка
Как было сказано выше, общее уравнение прямой имеет вид 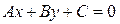 . Прямые называют также кривыми первого порядка, так как в их общее уравнение координаты . Прямые называют также кривыми первого порядка, так как в их общее уравнение координаты  и и  входят в первой степени. Рассмотрим теперь кривые, в уравнение которых, кроме первых степеней координат входят в первой степени. Рассмотрим теперь кривые, в уравнение которых, кроме первых степеней координат  и и  , входят и их квадраты, а также произведение координат , входят и их квадраты, а также произведение координат  . Такие кривые называются кривыми второго порядка. Итак, к ривые второго порядка − это кривые, уравнение которых имеет вид: . Такие кривые называются кривыми второго порядка. Итак, к ривые второго порядка − это кривые, уравнение которых имеет вид:
(1)  , ,
где А, В, С, D, E и F − произвольные числа (первые три – не все равны нулю, конечно, иначе опять получится уравнение прямой). Как бы мы ни меняли числа А, В и С в общем уравнении прямой  , все равно будем получать уравнения различных прямых на плоскости. А какого типа кривые могут получаться, если перебирать различные комбинации чисел А, В, С, D, E и F в уравнении кривых второго порядка (1)? Оказывается, что уравнение (1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (окружность – частный случай), гиперболу и параболу. Изучению этих кривых в "удобной" системе координат и займемся. , все равно будем получать уравнения различных прямых на плоскости. А какого типа кривые могут получаться, если перебирать различные комбинации чисел А, В, С, D, E и F в уравнении кривых второго порядка (1)? Оказывается, что уравнение (1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (окружность – частный случай), гиперболу и параболу. Изучению этих кривых в "удобной" системе координат и займемся.
Окружность
 Определение окружности известно из школьного курса математики. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Используя формулу расстояния Определение окружности известно из школьного курса математики. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Используя формулу расстояния
|


 Даны уравнения (общие) двух прямых
Даны уравнения (общие) двух прямых  и
и  . Требуется (не строя их) найти координаты точки их пересечения М (см. рисунок). Поскольку эта точка лежит на прямой
. Требуется (не строя их) найти координаты точки их пересечения М (см. рисунок). Поскольку эта точка лежит на прямой  , то ее координаты
, то ее координаты  и
и 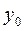 должны удовлетворять уравнению этой прямой, т.е. должно выполняться равенство:
должны удовлетворять уравнению этой прямой, т.е. должно выполняться равенство:  . По аналогичным соображениям числа
. По аналогичным соображениям числа  и
и 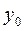 должны удовлетворять и уравнению второй прямой:
должны удовлетворять и уравнению второй прямой: 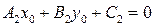 . Таким образом, координаты
. Таким образом, координаты  и
и 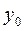 точки их пересечения
точки их пересечения 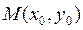 удовлетворяют системе уравнений
удовлетворяют системе уравнений

 . Найдем вид формул в уравнении (1) для прямой линии. Рассмотрим два случая.
. Найдем вид формул в уравнении (1) для прямой линии. Рассмотрим два случая. I. Сначала рассмотрим случай, когда прямая
I. Сначала рассмотрим случай, когда прямая  (левая часть рисунка). Ясно, что ее уравнение должно содержать параметры, характеризующие положение именно данной прямой. Чем же можно характеризовать положение этой прямой? Поскольку она не параллельна оси
(левая часть рисунка). Ясно, что ее уравнение должно содержать параметры, характеризующие положение именно данной прямой. Чем же можно характеризовать положение этой прямой? Поскольку она не параллельна оси  – то число, которое соответствует точке пересечения прямой с осью
– то число, которое соответствует точке пересечения прямой с осью 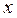 . Вот если кроме числа
. Вот если кроме числа  , под которым прямая пересекает ось
, под которым прямая пересекает ось  ,
, называется угловым коэффициентом прямой l, а само уравнение (2) называется у равнением прямой с угловым коэффициентом. Итак, уравнение любой прямой, не параллельной оси
называется угловым коэффициентом прямой l, а само уравнение (2) называется у равнением прямой с угловым коэффициентом. Итак, уравнение любой прямой, не параллельной оси  ,
,  имеет совсем простой вид
имеет совсем простой вид  , а формула
, а формула 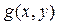 − тоже простого вида:
− тоже простого вида:  .
. в точке, соответствующей числу 3, и пересекает ось
в точке, соответствующей числу 3, и пересекает ось  под углом
под углом  .
. . По условию задачи
. По условию задачи  , а
, а  . Поэтому угловой коэффициент
. Поэтому угловой коэффициент  . Подставляя, получим уравнение прямой
. Подставляя, получим уравнение прямой 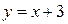 .
. и
и  , а потому уравнение соответствующей прямой имеет вид
, а потому уравнение соответствующей прямой имеет вид  , где
, где 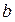 − некоторое число. В этом случае
− некоторое число. В этом случае  , а отсюда следует (если вспомнить значения тангенса), что
, а отсюда следует (если вспомнить значения тангенса), что  . Отсюда следует, что прямая с та
. Отсюда следует, что прямая с та  ким уравнением составляет с осью
ким уравнением составляет с осью 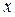 нулевой угол. Нулевой угол составляют между собой только параллельные либо совпадающие прямые. Поэтому уравнение
нулевой угол. Нулевой угол составляют между собой только параллельные либо совпадающие прямые. Поэтому уравнение  (т.е. когда
(т.е. когда  ) есть уравнение прямой, совпадающей с осью
) есть уравнение прямой, совпадающей с осью  (например,
(например,  или
или 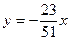 ). То, что
). То, что 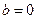 , означает, что прямая пересекает ось
, означает, что прямая пересекает ось 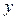 в начале координат. Таким образом, уравнение вида
в начале координат. Таким образом, уравнение вида  есть уравнение прямой, проходящей через начало координат (см. рисунок).
есть уравнение прямой, проходящей через начало координат (см. рисунок). и
и  не существуют в том смысле, как мы раньше их определили. Числа
не существуют в том смысле, как мы раньше их определили. Числа 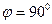 , а
, а 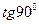 , как известно, не определен. Как же записать уравнение такой прямой? Все же ось
, как известно, не определен. Как же записать уравнение такой прямой? Все же ось  . Вспомним, что уравнение любой линии это (по определению) соотношение, которому должны удовлетворять координаты
. Вспомним, что уравнение любой линии это (по определению) соотношение, которому должны удовлетворять координаты  любой точки этой линии. Глядя на рисунок, изображающий обсуждаемую прямую, легко понять, что все точки прямой подчинены единственному требованию: их
любой точки этой линии. Глядя на рисунок, изображающий обсуждаемую прямую, легко понять, что все точки прямой подчинены единственному требованию: их  . Таким образом, уравнение любой прямой, параллельной оси у, имеет вид
. Таким образом, уравнение любой прямой, параллельной оси у, имеет вид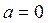 , то прямая совпадет с осью у. Поэтому
, то прямая совпадет с осью у. Поэтому  есть уравнение прямой, совпадающей с осью
есть уравнение прямой, совпадающей с осью 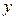 .
.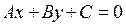 ,
,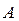 ,
, 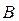 и
и  − некоторые числа (для разных прямых − разные). Уравнение вида (4) называется общим уравнением прямой. Меняя всевозможным образом числа
− некоторые числа (для разных прямых − разные). Уравнение вида (4) называется общим уравнением прямой. Меняя всевозможным образом числа 
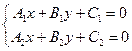 .
. и
и  есть решение системы уравнений (5).
есть решение системы уравнений (5). и
и  .
.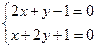 и решаем ее. Если числа в уравнениях системы перенести в правую часть, получим типичный вид системы двух линейных уравнений с двумя неизвестными. Хотя ранее мы проходили серьезные методы решения подобных систем, данную системы решим «школьными» методами, выражая из одного уравнения одну неизвестную через другую и подставляя в оставшееся уравнение. Из первого уравнения
и решаем ее. Если числа в уравнениях системы перенести в правую часть, получим типичный вид системы двух линейных уравнений с двумя неизвестными. Хотя ранее мы проходили серьезные методы решения подобных систем, данную системы решим «школьными» методами, выражая из одного уравнения одну неизвестную через другую и подставляя в оставшееся уравнение. Из первого уравнения 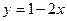 , подставляя во второе уравнение
, подставляя во второе уравнение  и решая, получим
и решая, получим 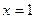 , а потому
, а потому  . Итак, прямые пересекаются в точке
. Итак, прямые пересекаются в точке  .
. Пусть уравнение прямой имеет вид
Пусть уравнение прямой имеет вид  (уравнение любой прямой можно представить в таком виде). Требуется построить эту прямую. Построение прямых линий облегчается тем, что надо узнать положение лишь двух любых ее точек (через любые две точки проходит единственная прямая). Положение каждой точки определяется двумя координатами. Таким образом, по уравнению прямой надо найти 4 неизвестных числа – по две координаты каждой точки. Воспользуемся тем, что эта пара точек может быть любой, и будем искать те точки прямой, для определения положения которых неизвестных надо будет находить меньше. Такими точками являются точки пересечения прямой с осями координат (точки C и D на рисунке). Значение одной из координат этих точек известно заранее, так как точки лежат на осях координат. Ясно, что точка С имеет нулевую первую координату, а точка D − вторую. Поэтому для определения положения точек С и D надо будет найти только 2 числа − их оставшиеся координаты. Найдем координаты точки С. Эта точка является точкой пересечения данной прямой и прямой, совпадающей с осью у. По выше выведенному правилу для получения координат точки С надо решить систему (5), состоящую из уравнения данной прямой и уравнения прямой, совпадающей с осью у. Ранее мы получали уравнение такой прямой:
(уравнение любой прямой можно представить в таком виде). Требуется построить эту прямую. Построение прямых линий облегчается тем, что надо узнать положение лишь двух любых ее точек (через любые две точки проходит единственная прямая). Положение каждой точки определяется двумя координатами. Таким образом, по уравнению прямой надо найти 4 неизвестных числа – по две координаты каждой точки. Воспользуемся тем, что эта пара точек может быть любой, и будем искать те точки прямой, для определения положения которых неизвестных надо будет находить меньше. Такими точками являются точки пересечения прямой с осями координат (точки C и D на рисунке). Значение одной из координат этих точек известно заранее, так как точки лежат на осях координат. Ясно, что точка С имеет нулевую первую координату, а точка D − вторую. Поэтому для определения положения точек С и D надо будет найти только 2 числа − их оставшиеся координаты. Найдем координаты точки С. Эта точка является точкой пересечения данной прямой и прямой, совпадающей с осью у. По выше выведенному правилу для получения координат точки С надо решить систему (5), состоящую из уравнения данной прямой и уравнения прямой, совпадающей с осью у. Ранее мы получали уравнение такой прямой: 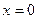 . Поэтому координаты точки С можно найти из системы:
. Поэтому координаты точки С можно найти из системы:  . Аналогичные рассуждения приводят к выводу, что координаты точки D можно найти из системы:
. Аналогичные рассуждения приводят к выводу, что координаты точки D можно найти из системы:  . Решив эти системы, определим положение точек С и D на осях координат, а затем через эти точки проведем прямую, которая и будет искомой.
. Решив эти системы, определим положение точек С и D на осях координат, а затем через эти точки проведем прямую, которая и будет искомой. .
. Решение. По полученному правилу координаты точки С пересечения этой прямой с осью у определяются решением системы уравнений
Решение. По полученному правилу координаты точки С пересечения этой прямой с осью у определяются решением системы уравнений  . Ее решение: x=0, y=2, а потому С(0, 2). Координаты точки D пересечения этой прямой с осью х определяются решением системы уравнений
. Ее решение: x=0, y=2, а потому С(0, 2). Координаты точки D пересечения этой прямой с осью х определяются решением системы уравнений  . Ее решение:
. Ее решение:  ,
,  , а потому
, а потому  . Осталось отметить на координатной плоскости эти точки с известными координатами и провести через них прямую (на рисунке).
. Осталось отметить на координатной плоскости эти точки с известными координатами и провести через них прямую (на рисунке). ), то договоримся, какой из них будем считать углом между прямыми. Углом между прямыми называется острый (или прямой) угол из двух смежных углов, образуемых при пересечении этих прямых (если прямые параллельны, то угол между ними считается равным нулю). На рисунке (выше, который иллюстрировал точку пересечения прямых) это угол обозначен буквой
), то договоримся, какой из них будем считать углом между прямыми. Углом между прямыми называется острый (или прямой) угол из двух смежных углов, образуемых при пересечении этих прямых (если прямые параллельны, то угол между ними считается равным нулю). На рисунке (выше, который иллюстрировал точку пересечения прямых) это угол обозначен буквой  . Если уравнения прямых имеют вид уравнений с угловыми коэффициентами
. Если уравнения прямых имеют вид уравнений с угловыми коэффициентами 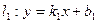 ,
, 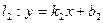 , то можно вывести формулу для тангенса угла между прямыми:
, то можно вывести формулу для тангенса угла между прямыми: ,
, 
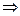
 .
. и
и  то формула выглядит так:
то формула выглядит так:  ,
, 
 .
. .
. , заданными уравнениями
, заданными уравнениями  и
и  .
. . Поэтому угловой коэффициент первой прямой
. Поэтому угловой коэффициент первой прямой 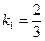 . Из уравнения второй прямой видно, что ее угловой коэффициент
. Из уравнения второй прямой видно, что ее угловой коэффициент  . По формуле (6) получаем
. По формуле (6) получаем  . Вспоминая значения тангенса известных углов, получаем, что угол меду прямыми
. Вспоминая значения тангенса известных углов, получаем, что угол меду прямыми  .
. . Поэтому для применения формулы (7) получаем такие значения параметров:
. Поэтому для применения формулы (7) получаем такие значения параметров:  ,
, 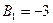 ,
,  ,
,  . Подставляя их в формулу (7), получаем
. Подставляя их в формулу (7), получаем  . Вывод тот же:
. Вывод тот же:  или
или  , тогда угол между ними
, тогда угол между ними  , а потому и
, а потому и  . Но по формуле (6):
. Но по формуле (6): 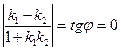 , поэтому
, поэтому  . Дробь равна нулю, если ее числитель равен нулю, а потому
. Дробь равна нулю, если ее числитель равен нулю, а потому 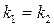 . Итак, параллельность прямых равносильна равенству их угловых коэффициентов. Выведем теперь условие перпендикулярности прямых с уравнениями
. Итак, параллельность прямых равносильна равенству их угловых коэффициентов. Выведем теперь условие перпендикулярности прямых с уравнениями  , то угол между ними
, то угол между ними  не существует (тангенс равен синус делить на косинус, а
не существует (тангенс равен синус делить на косинус, а  , но на 0 делить нельзя). Поскольку по формуле (6):
, но на 0 делить нельзя). Поскольку по формуле (6):  , то дробь
, то дробь  тоже не должна существовать. Дробь не существует только в том случае, когда ее знаменатель равен 0. Поэтому
тоже не должна существовать. Дробь не существует только в том случае, когда ее знаменатель равен 0. Поэтому 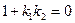 , а потому
, а потому  . Таким образом перпендикулярность прямых равносильна тому, что их угловые коэффициенты в произведении дают
. Таким образом перпендикулярность прямых равносильна тому, что их угловые коэффициенты в произведении дают  . Аналогично выводятся условия параллельности и перпендикулярности прямых, заданных своими общими уравнениями с использованием формулы (7).
. Аналогично выводятся условия параллельности и перпендикулярности прямых, заданных своими общими уравнениями с использованием формулы (7). ,
,  ,
,  .
.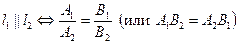 ,
,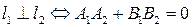 .
. вместо
вместо 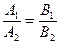 в (9) удобнее применять, если одно из чисел
в (9) удобнее применять, если одно из чисел 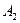 или
или  в знаменателях обращается в 0.
в знаменателях обращается в 0.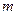 прямые
прямые  и
и  параллельны, а при каком перпендикулярны.
параллельны, а при каком перпендикулярны. . Поскольку теперь обе прямые заданы своими общими уравнениями, то используем критерий (9). По этому критерию прямые с уравнениями
. Поскольку теперь обе прямые заданы своими общими уравнениями, то используем критерий (9). По этому критерию прямые с уравнениями  , т.е. при
, т.е. при 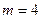 . По этому же критерию (9) прямые перпендикулярны, если
. По этому же критерию (9) прямые перпендикулярны, если  , т.е. при
, т.е. при 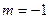 .
. и перпендикулярную прямой
и перпендикулярную прямой  .
. . Осталось найти числа
. Осталось найти числа  и
и  . Поскольку искомая прямая
. Поскольку искомая прямая  в их уравнениях. Поэтому для перпендикулярности прямых должно выполняться условие:
в их уравнениях. Поэтому для перпендикулярности прямых должно выполняться условие:  , откуда
, откуда  (отметим, что если бы в задаче надо было бы строить уравнение прямой
(отметим, что если бы в задаче надо было бы строить уравнение прямой  ). Таким образом, уравнение прямой
). Таким образом, уравнение прямой  , осталось найти число
, осталось найти число 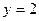 в уравнение прямой, получим
в уравнение прямой, получим  , откуда
, откуда 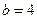 . Подставляя найденное
. Подставляя найденное 
 .
. При решении задач часто возникает необходимость найти уравнение прямой, если известно положение (т.е. координаты) двух ее точек. Поскольку через любые 2 точки проходит единственная прямая, то положение двух точек должно полностью определять положение всей прямой, а потому и ее уравнение. Пусть известны двух точек
При решении задач часто возникает необходимость найти уравнение прямой, если известно положение (т.е. координаты) двух ее точек. Поскольку через любые 2 точки проходит единственная прямая, то положение двух точек должно полностью определять положение всей прямой, а потому и ее уравнение. Пусть известны двух точек  и
и  некоторой прямой
некоторой прямой  .
. . Формулу (10) можно получить, если подставить в уравнение прямой
. Формулу (10) можно получить, если подставить в уравнение прямой 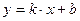 поочередно координаты обеих точек и решить полученную систему относительно параметров
поочередно координаты обеих точек и решить полученную систему относительно параметров  и
и  .
. ,
,  ,
, 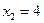 ,
, 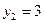 . Подставляя их в (10), получаем уравнение прямой
. Подставляя их в (10), получаем уравнение прямой 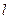 :
: 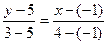 или
или  . Поэтому
. Поэтому  , а после раскрытия скобок
, а после раскрытия скобок  . Перенося теперь все в левую часть, получим общее уравнение искомой прямой
. Перенося теперь все в левую часть, получим общее уравнение искомой прямой  .
.
 и точку пересечения прямых
и точку пересечения прямых  и
и  Решение. На рисунке схематически изображены данные задачи и искомая прямая
Решение. На рисунке схематически изображены данные задачи и искомая прямая 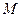 ) известны по условию. Осталось найти координаты какой-нибудь другой ее точки, чтобы можно было бы воспользоваться (10). По условию прямая
) известны по условию. Осталось найти координаты какой-нибудь другой ее точки, чтобы можно было бы воспользоваться (10). По условию прямая  точку пересечения прямых
точку пересечения прямых  :
:  . Таким образом, необходимо найти уравнение прямой
. Таким образом, необходимо найти уравнение прямой  ,
, 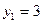 ,
, 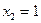 ,
,  . Подставляя их в (10), получаем уравнение прямой
. Подставляя их в (10), получаем уравнение прямой 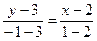 или
или  . Умножая обе части на
. Умножая обе части на  , получим
, получим  . Перенося теперь тройку из левой части в правую, получим уравнение искомой прямой
. Перенося теперь тройку из левой части в правую, получим уравнение искомой прямой 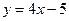 .
.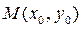 и общее уравнение прямой
и общее уравнение прямой  , то искомое расстояние вычисляется по формуле:
, то искомое расстояние вычисляется по формуле: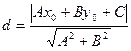 .
. до прямой с уравнением
до прямой с уравнением  . По формуле (11) получаем, что искомое расстояние
. По формуле (11) получаем, что искомое расстояние  .
.
 :
:  ,
,  ,
,  . Найти длину высоты из вершины А.
. Найти длину высоты из вершины А.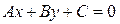 . Прямые называют также кривыми первого порядка, так как в их общее уравнение координаты
. Прямые называют также кривыми первого порядка, так как в их общее уравнение координаты  . Такие кривые называются кривыми второго порядка. Итак, к ривые второго порядка − это кривые, уравнение которых имеет вид:
. Такие кривые называются кривыми второго порядка. Итак, к ривые второго порядка − это кривые, уравнение которых имеет вид: ,
, , все равно будем получать уравнения различных прямых на плоскости. А какого типа кривые могут получаться, если перебирать различные комбинации чисел А, В, С, D, E и F в уравнении кривых второго порядка (1)? Оказывается, что уравнение (1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (окружность – частный случай), гиперболу и параболу. Изучению этих кривых в "удобной" системе координат и займемся.
, все равно будем получать уравнения различных прямых на плоскости. А какого типа кривые могут получаться, если перебирать различные комбинации чисел А, В, С, D, E и F в уравнении кривых второго порядка (1)? Оказывается, что уравнение (1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (окружность – частный случай), гиперболу и параболу. Изучению этих кривых в "удобной" системе координат и займемся. Определение окружности известно из школьного курса математики. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Используя формулу расстояния
Определение окружности известно из школьного курса математики. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Используя формулу расстояния 


